Chapter 02 : 1-Dimensional Motion

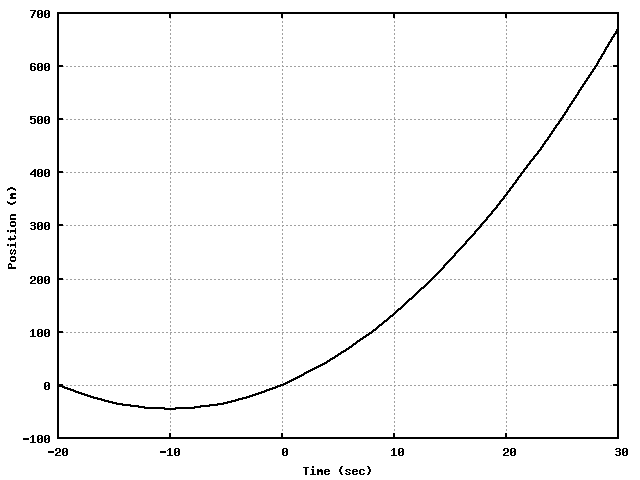
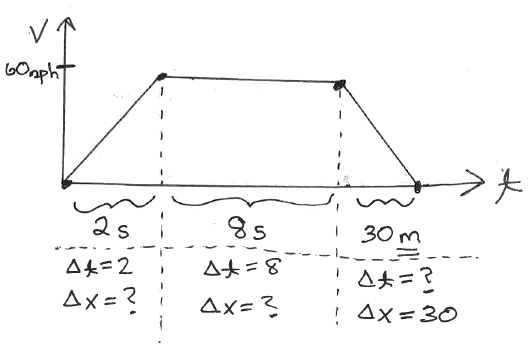
Overview

Iterative Process:
[measure] ➔ [model] ➔ [predict] ➔ ... (repeat)
Most of the course can be condensed into a single general equation:
Newton's Law:

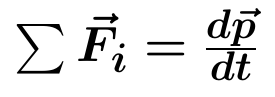
but we don't usually start there. By the end of the course we'll expand into several pages of equations, but by then it's useful to remember where it all starts.

Tacoma Narrows Bridge (1940)

short video (see around 30 sec in)
long video
Practical Engineering explanation

Level of Detail : the 'point mass' model

Reference Frames

Coordinate system used can affect the results of a measurement.

Any fixed or moving coordinate system is fine as long as no acceleration is involved.

We will see later that rotation itself creates an acceleration.

The Earth is rotating, so technically is not a 'good' reference frame but we routinely use it anyway.

Ball Drop

held at 4 feet (1.22 m) above the floor, it is actually moving slightly (8.7 X 10^-5 m/s) faster than the floor and will land about 0.04 millimeters to the East instead of directly below where it was released.
dropped (at rest) from the top of the tallest building, it would land over 50 cm away from where it 'should'

Do we need to worry about that???

Burj Khalifa (Dubai; 828 meters)

Ball Drop 'Experiment'

Drop a ball from about 4 feet (1.22 m) above the floor.
Coordinate System Choice:

Origin on floor directly below ball
Positive x axis pointing vertically upward

Record this 'x' coordinate as a function of time.

How far did the ball travel?

Displacement definition: Δx = x(t₂)-x(t₁)
(positive, zero, negative)

Distance
\[ s = \int_{t_1}^{t_2}ds \]

(zero or positive; can't be negative)
(Basically the odometer in your car: continuously accumulating)

What was the ball's displacement between t=0 and t=0.5 sec?
What distance did the ball travel between those times?
What was the ball's displacement between t=0.5 and t=1.0 sec?
What distance did the ball travel between those times?

POSITION : x(t)

How fast is the ball moving?

Average velocity: v_avg = Δx/Δt
Instantaneous velocity: v = dx/dt

What about speed? Ambiguous...

speed as |v|
speed as ds/dt (speedometer reading)

(A word best not used...)

What was the ball's average velocity between t=0 and t=0.5 sec?
What was the ball's average velocity between t=0.5 and t=1.0 sec?

VELOCITY : v(t) = dx/dt

Acceleration : rate of change of velocity

Average acceleration: a_avg = Δv/Δt
Instananeous acceleration: a = dv/dt

Note that for the ball (except for the momentary collision with the floor), a=-9.8 m/s²

ACCELERATION : a(t) = dv/dt

Can keep going: jerk is defined as da/dt, etc...

Example : Car Acceleration

My 2008 truck took 20 seconds to accelerate from 20 mph to 60 mph. Assuming the acceleration was constant:

What was the acceleration ?

How far did the truck travel during this interval?
What was the trucks average velocity?
Can we write an equation giving the truck's exact position as a function of time?

Motion with Constant Acceleration

a=dv/dt so if 'a' is constant what does the graph of v(t) have to look like?

v(t) = v_o+at

(our first EQUATION OF MOTION)

Another we can pick off this graph:
The average velocity between t=0 and some time t:
\[ v_{avg} = \frac{1}{2} ( v_o + v ) \]

but since v(t) = v_o+at we can also write this as:
\[ v_{avg} = v_o + \frac{1}{2} at \]

Position Equation of Motion

\[ v_{avg} = v_o + \frac{1}{2} at \]

\[ \Delta x = v_{avg} \Delta t \]

Making that substitution:
\[ x - x_o = ( v_o + \frac{1}{2}at ) t \]

Leading to:
\[ x = x_o + v_o t + \frac{1}{2}at^2 \]

What is the position equation of motion for the truck? x(t)=?

One Last Useful Equation

Everything above involved the time variable, but with the right algebraic steps, we can eliminate time:
v_avg = Δx/Δt so Δx=v_avgt
but:
v_avg = ( v_o + v )/2
v = v_o+at so t = ( v - v_o )/a
Making those substitutions, Δx=v_avgt becomes:
\[ \Delta x = ( \frac{ v+v_o }{2} )( \frac{ v-v_o }{a} ) \]

Expanding and rearranging:
\[ v^2 = v^2_o + 2 a \Delta x \]

As a check, recompute the truck's acceleration using the starting and ending velocities and the distance travelled:

Putting it All Together

A particular high performance car accelerates from rest to 60 MPH in 2.0 sec.
It continues at that velocity along a straight road for 8 sec, then slams on the brakes, bringing the car to a stop in 30 meters.

(a) What was the car's average velocity over this entire interval from start to stop?

Sketch of v(t)

Reference Frames
Coordinate system used can affect the results of a measurement. Any fixed or moving coordinate system is fine as long as no acceleration is involved. We will see later that rotation itself creates an acceleration.



The Earth is rotating, so technically is not a 'good' reference frame but we routinely use it anyway. Ball Drop held at 4 feet (1.22 m) above the floor, it is actually moving slightly (8.7 X 10^-5 m/s) faster than the floor and will land about 0.04 millimeters to the East instead of directly below where it was released. dropped (at rest) from the top of the tallest building, it would land over 50 cm away from where it 'should' Do we need to worry about that???	Burj Khalifa (Dubai; 828 meters)

Example : Car Acceleration
My 2008 truck took 20 seconds to accelerate from 20 mph to 60 mph. Assuming the acceleration was constant: What was the acceleration ? How far did the truck travel during this interval? What was the trucks average velocity? Can we write an equation giving the truck's exact position as a function of time?
Motion with Constant Acceleration
a=dv/dt so if 'a' is constant what does the graph of v(t) have to look like? v(t) = v_o+at (our first EQUATION OF MOTION) Another we can pick off this graph: The average velocity between t=0 and some time t: \[ v_{avg} = \frac{1}{2} ( v_o + v ) \] but since v(t) = v_o+at we can also write this as: \[ v_{avg} = v_o + \frac{1}{2} at \]
Position Equation of Motion
\[ v_{avg} = v_o + \frac{1}{2} at \] \[ \Delta x = v_{avg} \Delta t \] Making that substitution: \[ x - x_o = ( v_o + \frac{1}{2}at ) t \] Leading to: \[ x = x_o + v_o t + \frac{1}{2}at^2 \] What is the position equation of motion for the truck? x(t)=?
One Last Useful Equation
Everything above involved the time variable, but with the right algebraic steps, we can eliminate time: v_avg = Δx/Δt so Δx=v_avgt but: v_avg = ( v_o + v )/2 v = v_o+at so t = ( v - v_o )/a Making those substitutions, Δx=v_avgt becomes: \[ \Delta x = ( \frac{ v+v_o }{2} )( \frac{ v-v_o }{a} ) \] Expanding and rearranging: \[ v^2 = v^2_o + 2 a \Delta x \] As a check, recompute the truck's acceleration using the starting and ending velocities and the distance travelled:
Putting it All Together
A particular high performance car accelerates from rest to 60 MPH in 2.0 sec. It continues at that velocity along a straight road for 8 sec, then slams on the brakes, bringing the car to a stop in 30 meters. (a) What was the car's average velocity over this entire interval from start to stop?	Sketch of v(t)