Review:

 

Definitions
Position Displacement	\[ x(t) \] \[ \Delta x = x(t_2)-x(t_1) \]
Velocity (average) Velocity (instantaneous)	\[ v_{avg} = \frac{\Delta x}{\Delta t} \] \[ v = \frac{dx}{dt} \]
Acceleration (average) Acceleration (instantaneous)	\[ a_{avg} = \frac{\Delta v}{\Delta t} \] \[ a = \frac{dv}{dt} \]
1-D Equations of Motion ONLY valid when acceleration is CONSTANT
Velocity	\[ v(t) = v_o + at \]
Average Velocity	\[ v_{avg} = \frac{ v_o + v }{2} = v_o + \frac{1}{2}at \]
Position	\[ x(t) = x_o + v_o t + \frac{1}{2}at^2 \]
Useful shortcut	\[ v^2 = v^2_o + 2 a \Delta x \]

 

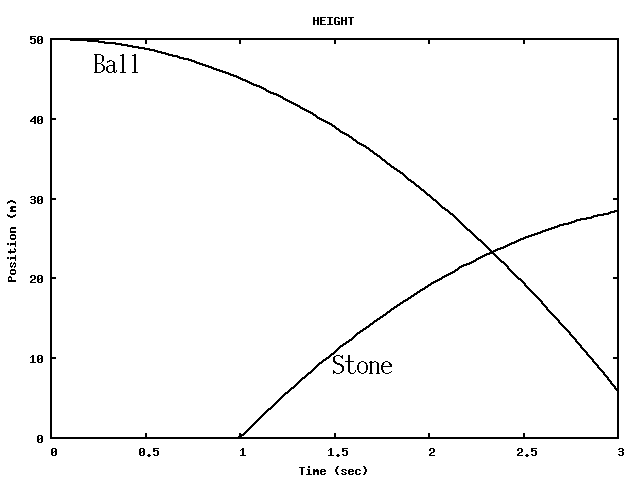
Free-Fall Motion
Definition : A object is moving under the influence of gravity (with no other forces present), which means it has an acceleration directed downward towards the earth (or moon, or other object). The magnitude of the acceleration due to gravity at the surface of the Earth is approximately |a| = g = 9.8 m/s2 The entity (symbol) g is always a positive constant. The acceleration may be either a=+9.8 m/s2 or a=-9.8 m/s2 depending on your choice of coordinate system. 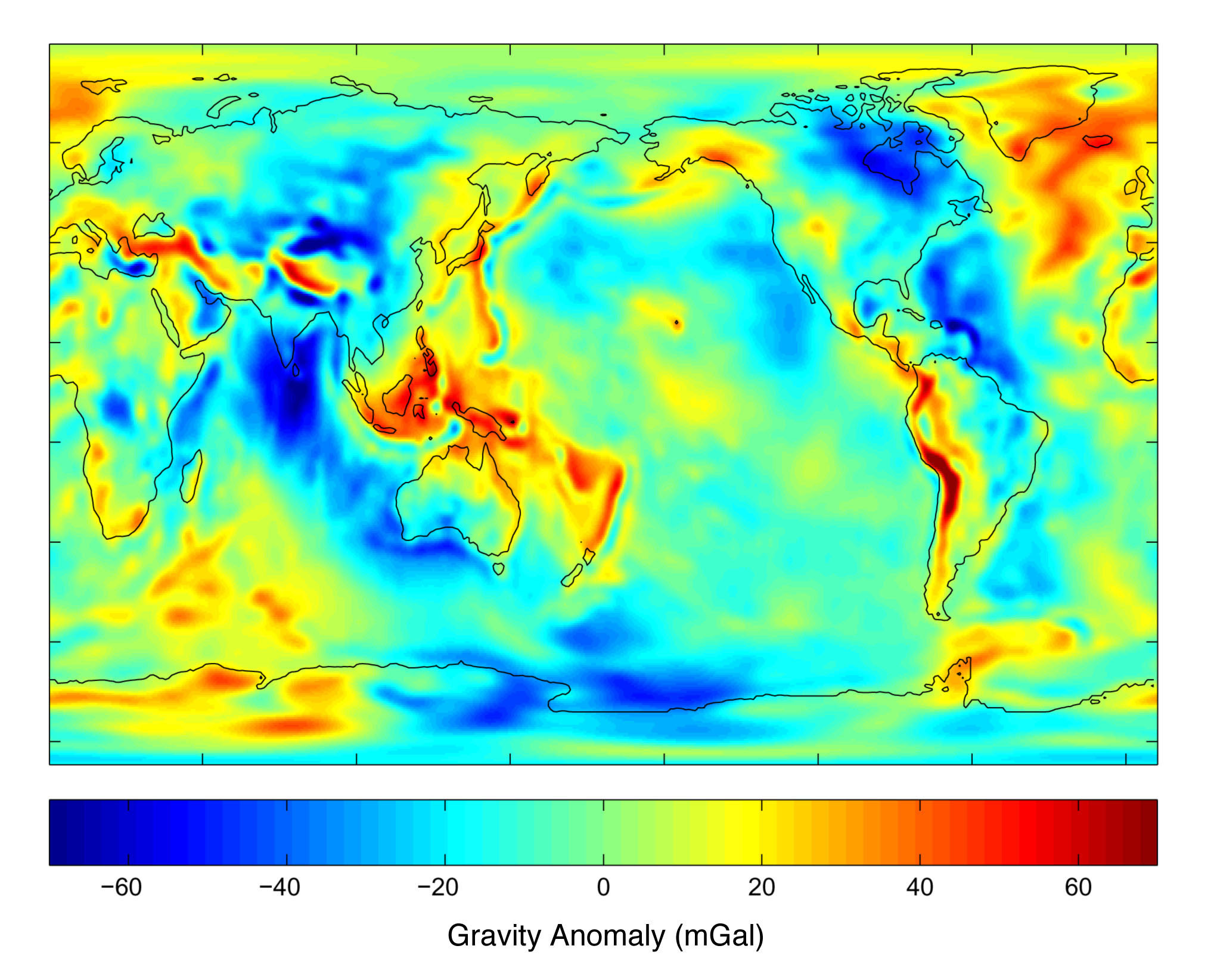The figure shows the slight variations of g around the Earth. Lowest: g=9.764 m/s2 : Nevado Huascaran mountain, Peru Highest: g=9.834 m/s2 : surface in Arctic Ocean Starkville: g=9.807 m/s2	Variations in the Earth's Gravity (units of 10-5 m/s2)
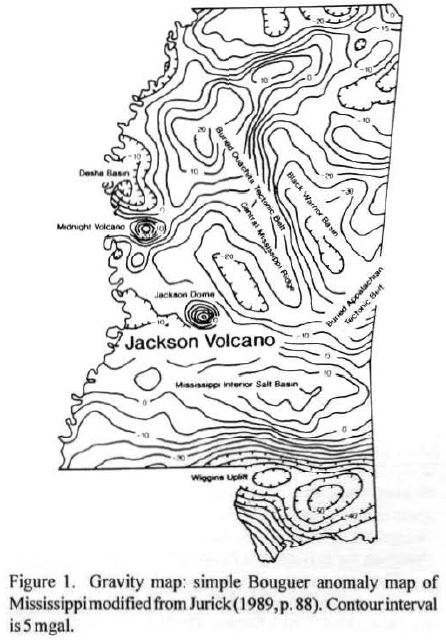
Gravity Survey of the state of Mississippi
Examples
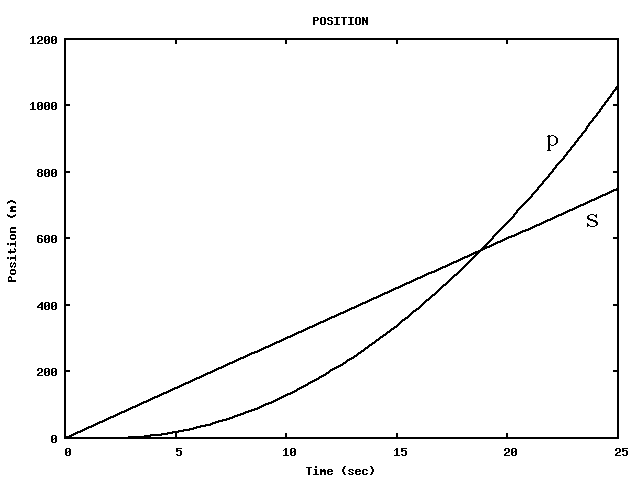
A ball is released (at rest) from a height of 2 meters above the floor. How much time does it take for the ball to hit the floor? How fast is the ball moving at that point?   (We'll solve this by finding the time first.)
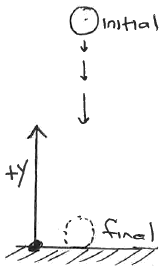
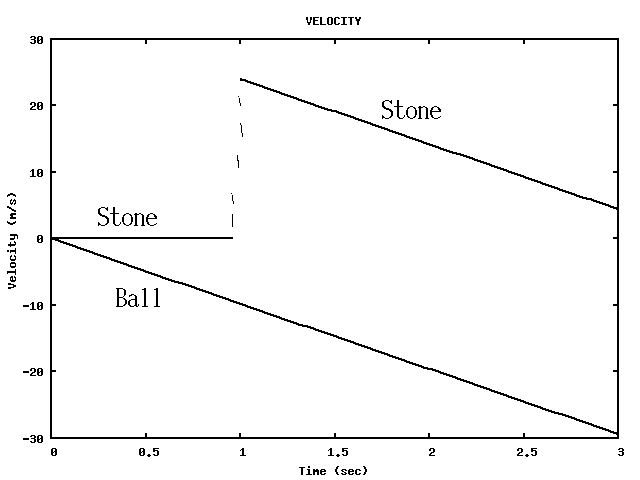
Let's redo the problem but this time: using a different coordinate system (with positive downward) solving for the velocity first then using that velocity to find the time
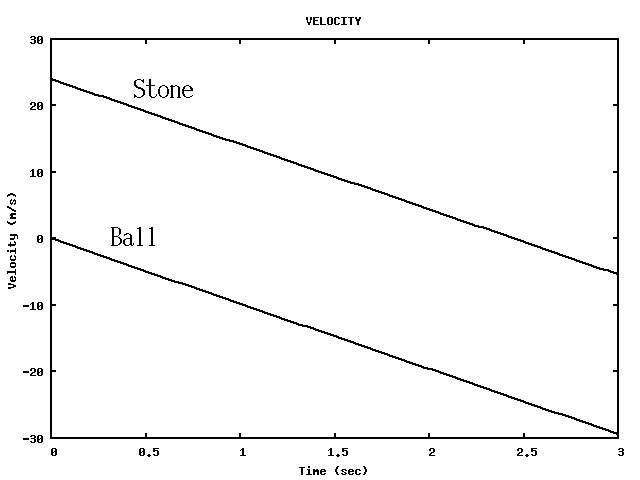
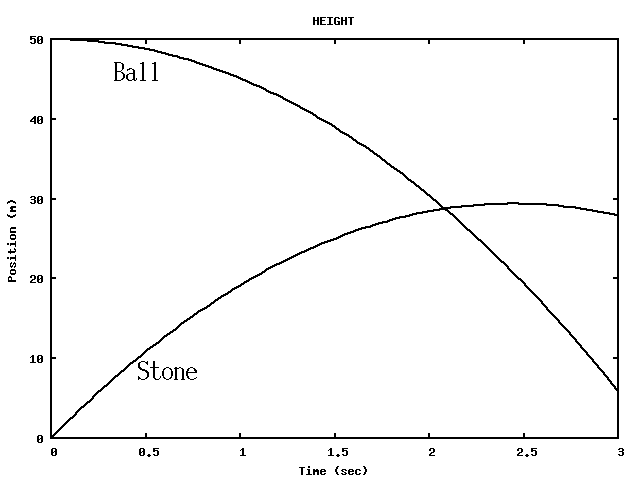
This time, suppose we throw the ball vertically upward at 4 m/s. How much time does it take for the ball to hit the floor? How fast is the ball moving at that point? Find the maximum height above the floor that the ball reaches.

 

Two Objects : Car Chase
A speeding car is travelling down a straight road at a constant speed of 30 m/s. A police car on the side of the road sees the speeder coming and at the instant the speeder passes the police car, the police car starts accelerating with an acceleration of 4 m/s2. The police car eventually catches up to the speeder:   (a) when does that happen?   (b) where does that happen?   (c) how fast is each vehicle moving at that time?

 

Car Chase with Delay
Let's look at a more realistic version of the same scenario. Suppose the police car doesn't start accelerating right away: instead, let's say it takes 2 seconds for the driver to react before starting to accelerate after the speeder. The police car will still eventually catch up to the speeder, but when and where does that happen now?
The problem here is that if we keep t=0 the same as before, we can't write an 'equation of motion' for the police car that covers the whole event. Their acceleration is not constant now: it's a=0 for two seconds, then a=4 m/s2 for the remainder of the event. How can we deal with that?

 

Two Objects in Free-Fall
A ball (B) is dropped from the top of a 50 meter high cliff. Simultaneously, a carefully aimed stone (S) is thrown straight up from the bottom of the cliff at a speed of 24 m/s. We observe that the stone and ball collide part-way up.     (a) How far above the base of the cliff does this happen?     (b) What velocities do the ball and stone have when they collide?

 

Two Objects in Free-Fall : with delay
A ball (B) is dropped from the top of a 50 meter high cliff. One second layer, a carefully aimed stone (S) is thrown straight up from the bottom of the cliff at a speed of 24 m/s in an attempt to intercept the ball before it hits the ground. Is it successful? If so:     (a) How far above the base of the cliff does this happen?     (b) What velocities do the ball and stone have when they collide?