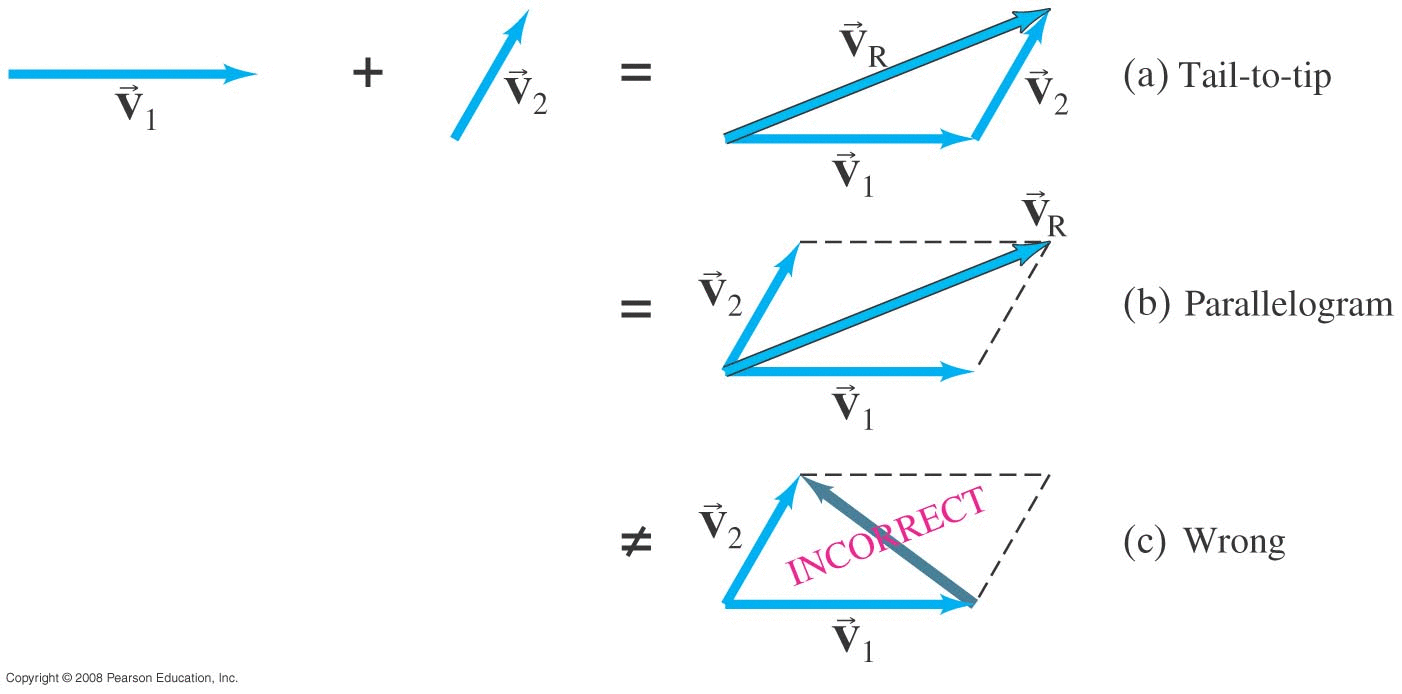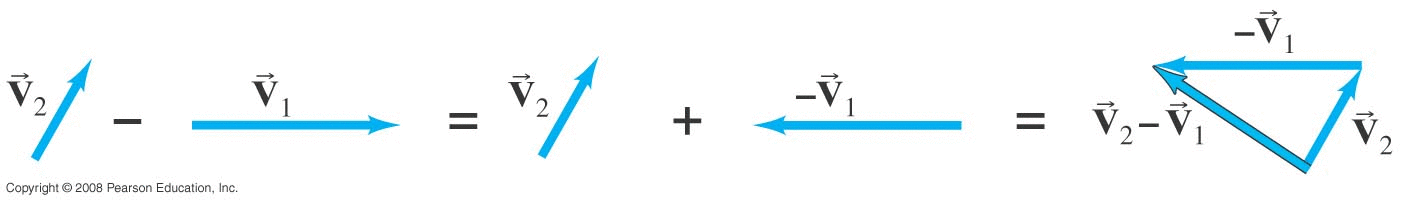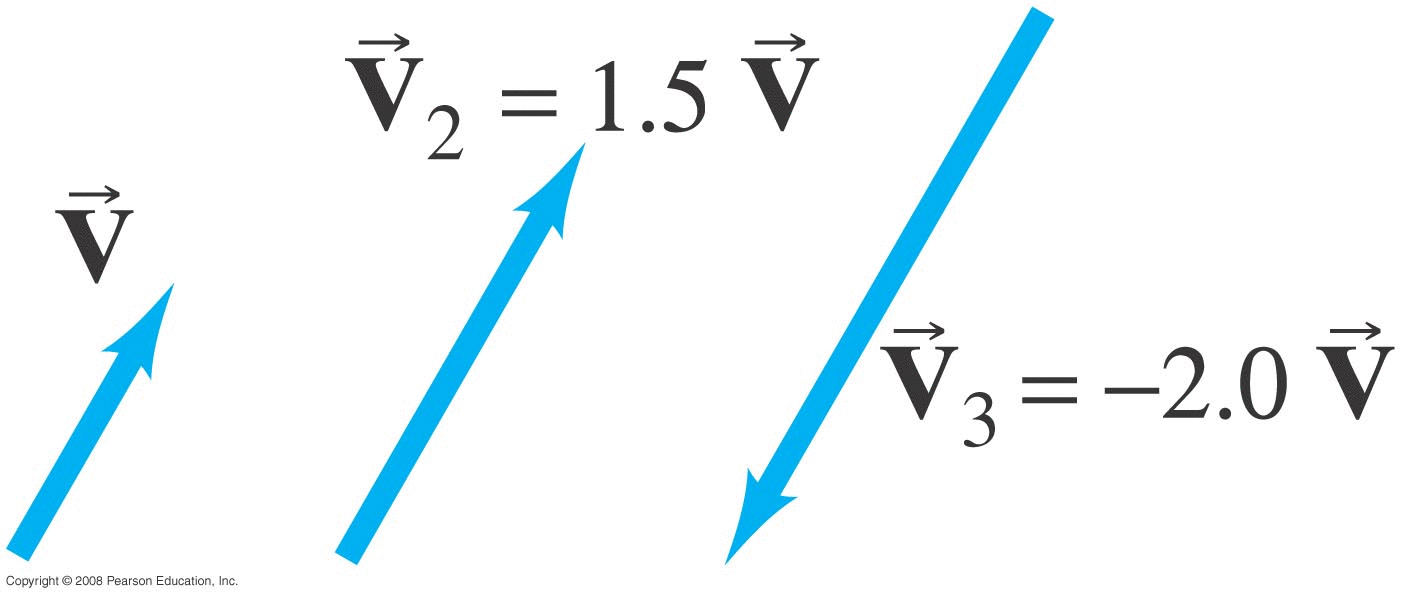|
A vector is a mathematical construct that
has a magnitude and a direction.
Technically, that's all it is: it isn't attached to
any particular location.
10 km to the northwest
5 MPH to the southeast
|

|
|
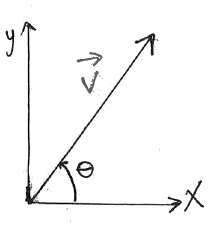
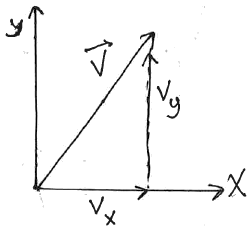
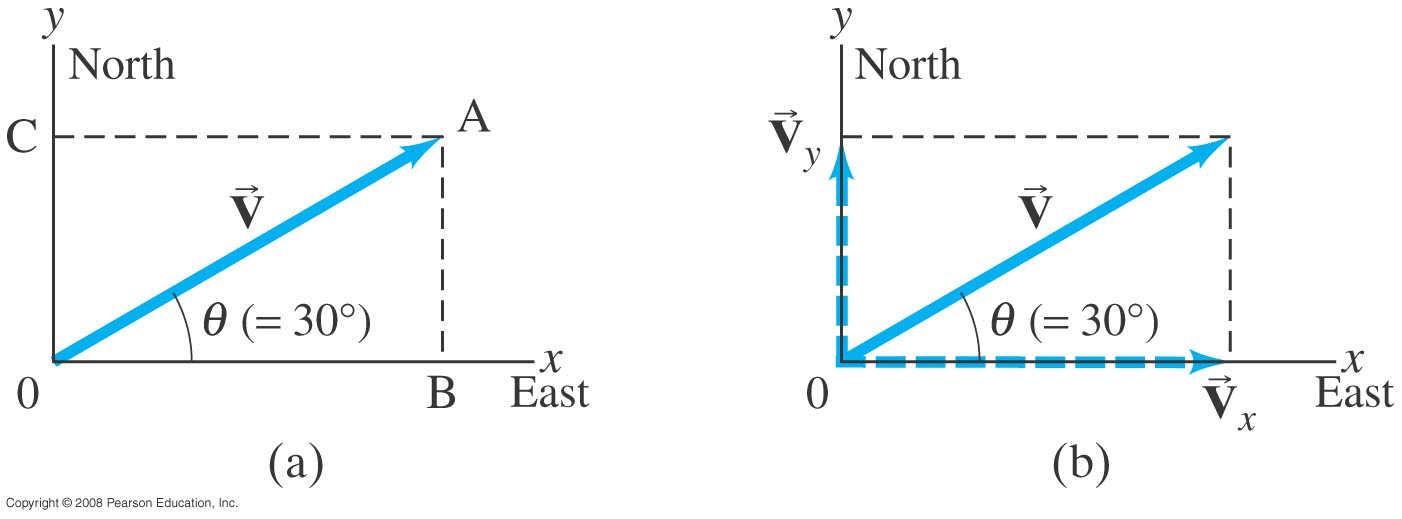
Conventionally, the magnitude of
a vector is denoted by using the same
symbol without the vector sign above the symbol:
Which leads to the polar coordinates representation of the vector:
\[ \vec{v} = ( v , \theta ) \] |
|
|
We'll see more of this in later slides, but mostly in this course
we'll be using a Cartesian representation
for vectors, which we'll see in the example on the next page.
|
|
Vector Addition |
|
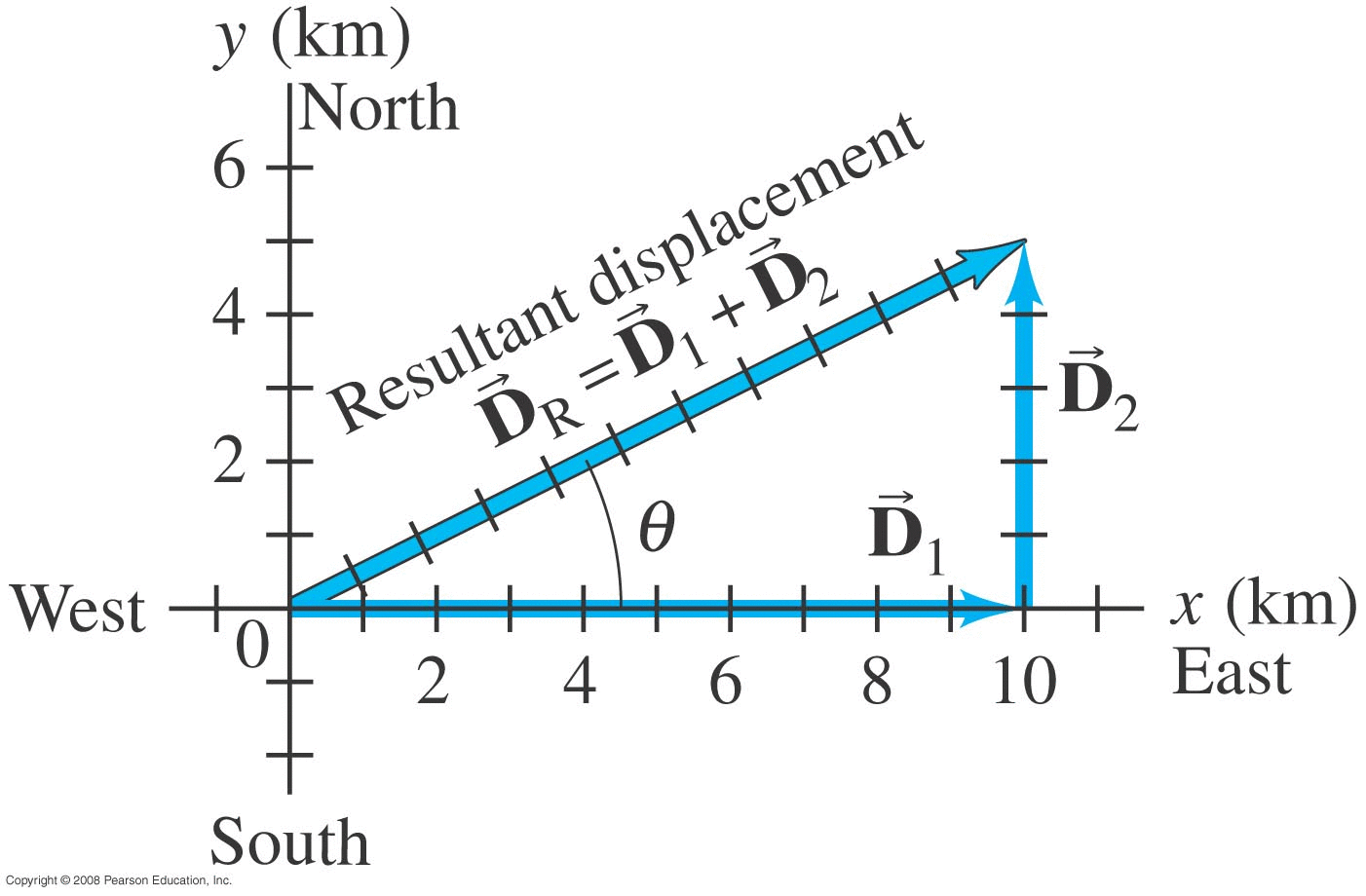
Suppose we walk 10 km to the East, then 5 km to the north?
In vector form:
Vector D1 = (10 km to the East)
Vector D2 = (5 km to the North)
Resultant vector:
\[ \vec{D}_1 + \vec{D}_2 = \vec{D}_R \] |
|
|
Suppose instead, we first walk 5 km to the north and then walk 10 km to the East?
Vector D1 = (10 km to the East)
Vector D2 = (5 km to the North)
Resultant vector:
\[ \vec{D}_2 + \vec{D}_1 = \vec{D}_R \] |

|
|
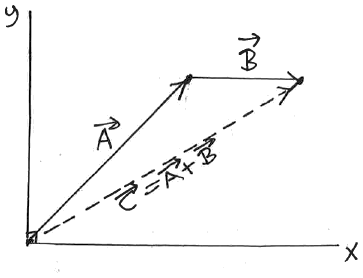
We arrive at the same place: Vector Addition is COMMUTATIVE.
|
|
Parallelogram Method for adding vectors
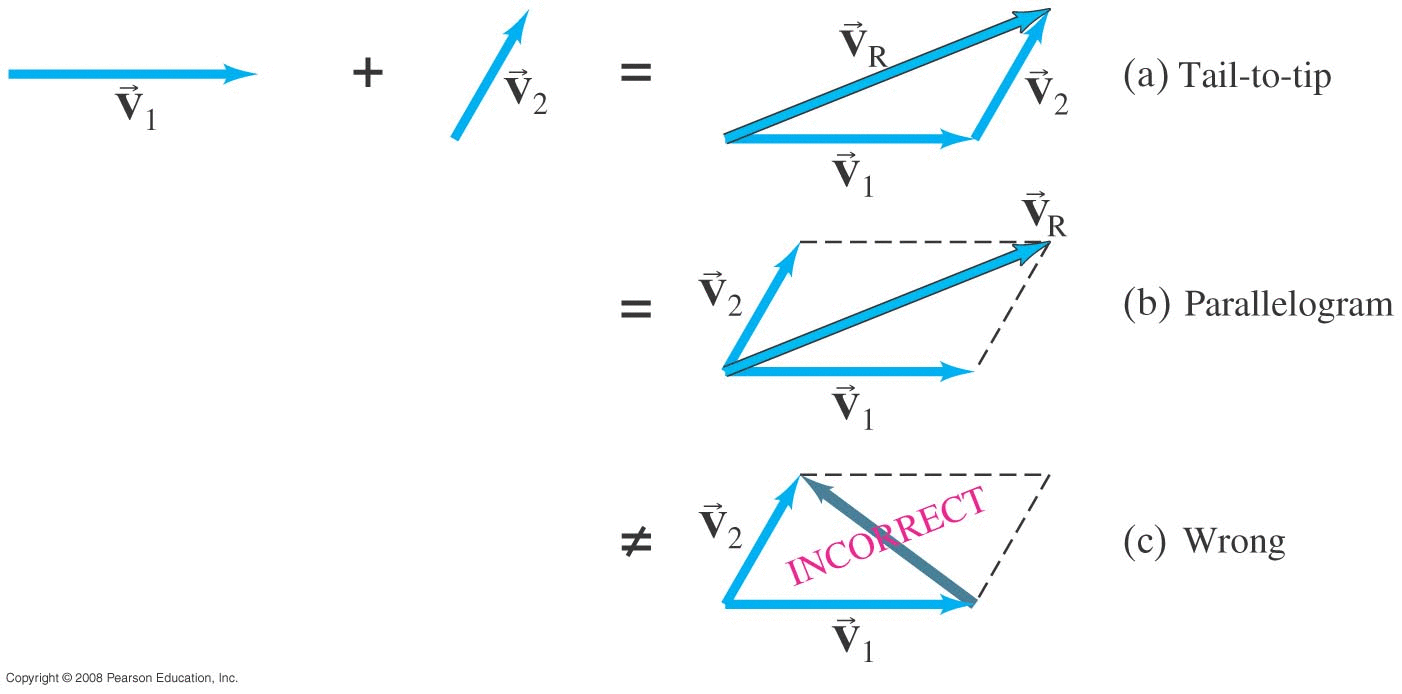
|
Example: Hiker |
|
A hiker leaves camp and walks 200 m to the northeast.
They then walk 100 m directly to the east.
Where are they now?
If someone wants to leave the
original camp location and walk directly to
where the hiker is now located, what vector would
give their distance and direction?)
|
|
|
Polar Representation (magnitude and direction) of the two segments: ( Let x='East' and y='North' )
\[ Leg~1 \hspace{2em} \vec{A} = (200~m,45^o) \]
\[ Leg~2 \hspace{2em} \vec{B} = (100~m,0^o) \]
\[ What~is~ \vec{A} + \vec{B} \]
|
Vector Math |
|
The negative of a vector is a vector with the same magnitude, but the opposite direction:
|
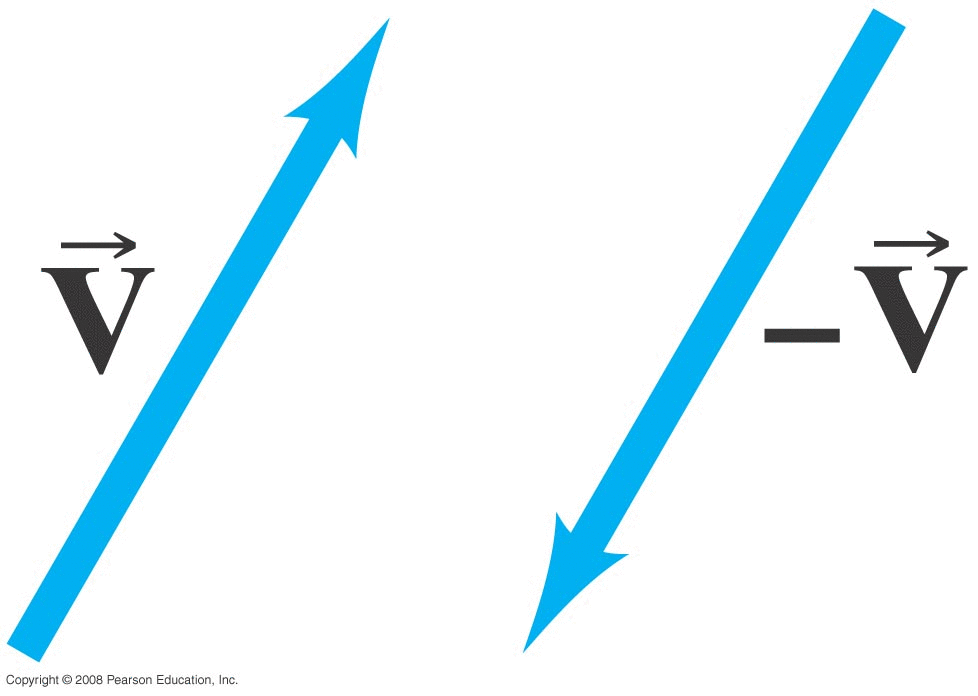
|
|
Subtraction can then be seen as adding the negative of a vector:
|
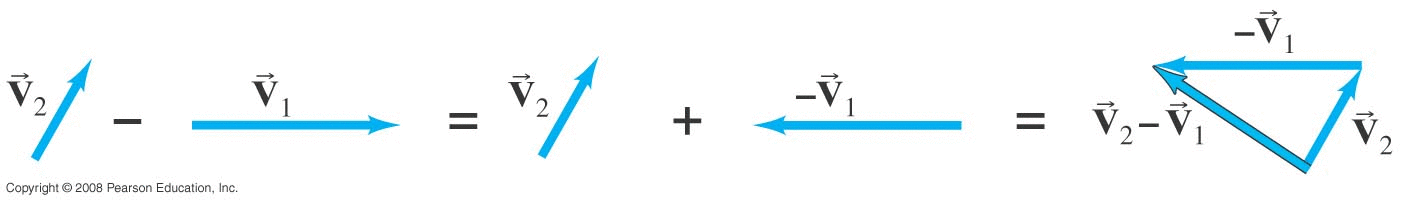
|
|
Multiplying a vector by a scalar yields a vector
in the same direction but whose magnitude has
been multiplied by that scalar:
|
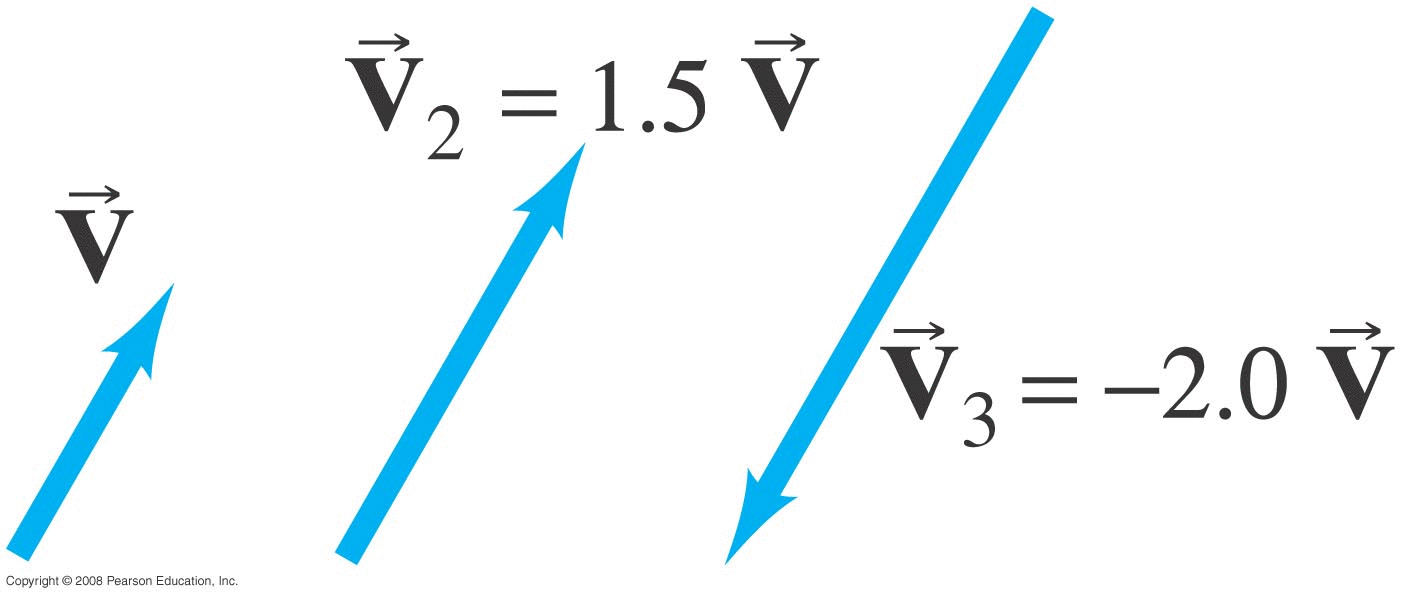
|
Unit Vector (Cartesian) Representation |
|
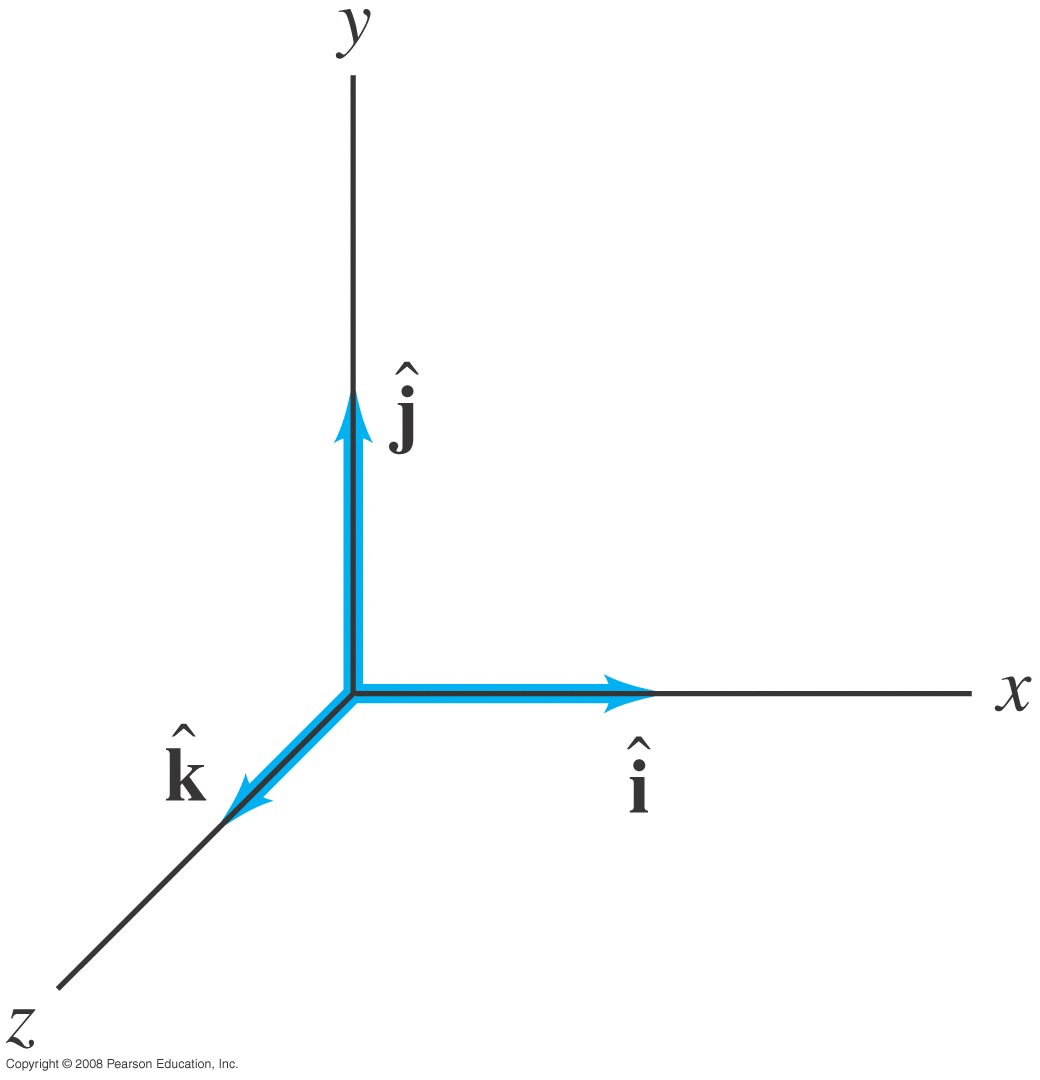
Short-hand for:
\[ \hat{i} = ~in~the~X~direction \]
\[ \hat{j} = ~in~the~Y~direction \]
\[ \hat{k} = ~in~the~Z~direction \]
Some fields use a different (better?) notation:
\[ \hat{x} = ~in~the~X~direction \]
\[ \hat{y} = ~in~the~Y~direction \]
\[ \hat{z} = ~in~the~Z~direction \]
Each denotes 'unit vectors' aligned with each coordinate axis.
No physical units are associated with them,
they just represent direction.
|
|
Components |
|
When we represent a vector using this unit-vector notation, a common convention
(which we will use) is to refer to the separate i,j,k parts that make up the vector
as being it's components, which are denoted using the same letter with
subscripts x,y,z.
This is called resolving a vector into its components.
\[ \vec{V} = V_x\hat{i} + V_y\hat{j} + V_z\hat{k} \] |
|
A notation you may encounter elsewhere:
Suppose we have a velocity vector of 10 m/s in the northeast direction.
If we divide that vector by its magnitude (the 10 m/s part, which we'd write as |v| or just v without
the vector symbol over it) we get a vector that just represents the direction ("northeast").
Since this vector has a magnitude of 1 and just contains direction,
it's given the same 'hat' notation:
\[ \frac{\vec{v}}{v} = \hat{v} \] so we can write any vector as:
\[ \vec{v} = v \hat{v} \] (Yes that looks obtuse and you probably won't encounter it outside of a math class...)
|
Example : Hiker |
|
Redo the "hiker" example, this time using vectors in this unit-vector notation.
|
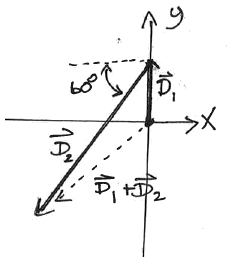
Example : Mail Carrier |
|
A rural mail carrier leaves the post office and drives:
(see figure at right).
What is her displacement from the post office?
Express the displacement in three forms:
Cartesian form (x,y,z)
Unit vector form
Polar coordinates (r,θ)
(This is an example in the textbook, but I've changed the numbers to illustrate
a problem with the inverse trig functions on your calculator!)
|
|