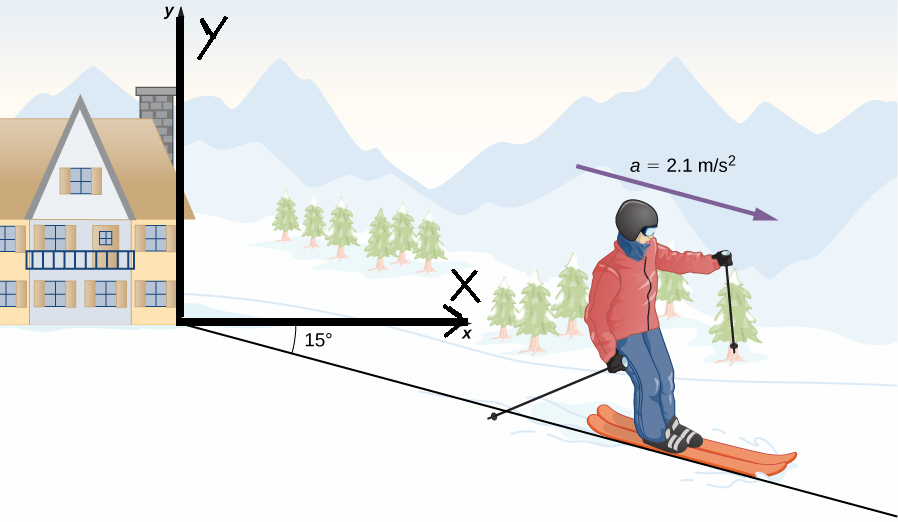
VECTORS
If we roll a ball off the edge of a table, it follows a path through the air on the way to the ground. The ball is no longer moving in a straight line, so we'll need to use a 2D or 3D coordinate system to fully describe it's motion. An object moving in a straight line only needs a single coordinate (x perhaps) to specify it's motion, but an object moving arbitrarily through space potentially needs x, y, and z to describe its position. This (x,y,z) collection is essentially the position vector of the object.
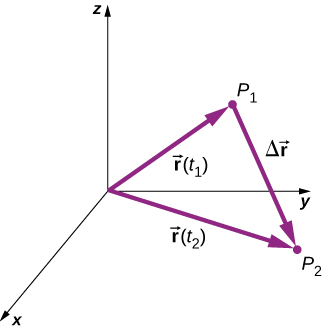
Position	Displacement
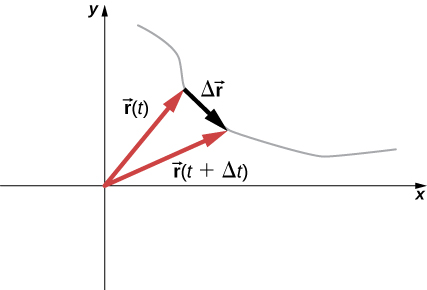
Velocity   Average Velocity \( \vec{v}_{avg} = \frac{ \Delta \vec{r} }{\Delta t} \)   Instantaneous Velocity \( \vec{v}(t) = \frac{ d\vec{r} }{dt} \) \( \vec{v}(t) = \frac{dx}{dt}\hat{i} + \frac{dy}{dt}\hat{j} + \frac{dz}{dt}\hat{k} \) \( \vec{v}(t) = v_x\hat{i} + v_y\hat{j} + v_z\hat{k} \)
Average Acceleration \( \vec{a}_{avg}(t) = \frac{ d\vec{v} }{dt} \)	Instantaneous Acceleration \( \vec{a}(t) = \frac{ d\vec{v} }{dt} \) \( \vec{a}(t) = \frac{dv_x}{dt}\hat{i} + \frac{dv_y}{dt}\hat{j} + \frac{dv_z}{dt}\hat{k} \) \( \vec{a}(t) = a_x\hat{i} + a_y\hat{j} + a_z\hat{k} \)
Constant Acceleration
\( \vec{a} \) is the slope of the \( \vec{v} \) 'graph' (in 2 or 3 dimensions) IF \( \vec{a} \) is constant, then \( \vec{v}(t) \) is a line (in space) such that \( d\vec{v}/dt = \vec{a} = constant \) Requires: \[ \vec{v}(t) = \vec{v}_o + \vec{a}t \]

 

1-D vs Vector Definitions and Equations
Location	x(t)	\( \vec{r}(t) \)
Displacement	\( \Delta x = x(t_2)-x(t_1) \)	\( \Delta \vec{r} = \vec{r}(t_2) - \vec{r}(t_1) \)
Average velocity	\( v_{avg} = \Delta x / \Delta t \)	\( \vec{v}_{avg} = \Delta \vec{r} / \Delta t \)
Instantaneous velocity	\( v = dx/dt \)	\( \vec{v} = d\vec{r}/dt \)
Average acceleration	\( a_{avg} = \Delta v / \Delta t \)	\( \vec{a}_{avg} = \Delta \vec{v} / \Delta t \)
Instantaneous acceleration	\( a = dv/dt \)	\( \vec{a} = d\vec{v}/dt \)
Constant Acceleration Equations of Motion
Velocity	\( v = v_o + at \)	\( \vec{v} = \vec{v}_o + \vec{a}t \)
Average Velocity	\( v_{avg} = \frac{1}{2}( v_o + v ) = v_o + \frac{1}{2}at \)	\( \vec{v}_{avg} = \frac{1}{2}( \vec{v}_o + \vec{v} ) = \vec{v}_o + \frac{1}{2}\vec{a}t \)
Position	\( x = x_o + v_{avg} t \)	\( \vec{r} = \vec{r}_o + \vec{v}_{avg} t \)
Position	\( x = x_o + v_o t + \frac{1}{2}at^2 \)	\( \vec{r} = \vec{r}_o + \vec{v}_o t + \frac{1}{2}\vec{a}t^2 \)
Shortcut	\( v^2 = v^2_o + 2 a \Delta x \)	\( v^2 = v^2_o + 2 a_x \Delta x + 2 a_y \Delta y + 2 a_z \Delta z \)
Each VECTOR equation is really THREE equations
Expanding out each term in:   \( \vec{v} = \vec{v}_o + \vec{a}t \)   \[ (v_x\hat{i} + v_y\hat{j} + v_z\hat{k}) = (v_{ox}\hat{i} + v_{oy}\hat{j} + v_{oz}\hat{k}) + ( a_x\hat{i} + a_y\hat{j} + a_z \hat{k})t \] and separating out the i,j,k components, this becomes THREE equations: \[ v_x = v_{ox} + a_x t \hspace{2em} v_y = v_{oy} + a_y t \hspace{2em} v_z = v_{oz} + a_z t \]   In practice then, 2-D and 3-D motion starts off with vector equations but calculators (and computers) rarely work directly on vector quantities, so we end up turning the problem into (potentially) three separate problems: what's happening in X, Y and Z separately.

 

Example : Skier sliding down a slope
A skier starts at rest and slides down a perfectly flat slope that is angled 15o below the horizontal. They are observed to have an acceleration of 2.1 m/s2 along the slope.   Four seconds later: (a) how far have they travelled? (b) how fast are they moving?
We'll work this problem twice: Using the coordinate system included in the figure. Using a coordinate system where the (X,Y) axes have been rotated so that X points down along the slope.

 

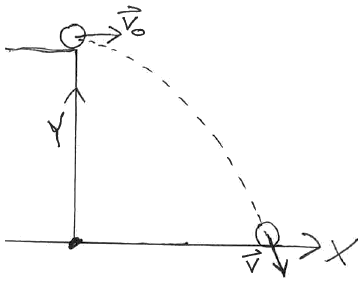
Example : Ball rolling off table
A ball moving (horizontally) at 2 m/s rolls off the side of a table that is 1.0 m above the floor.   Where will the ball land? How long does it take to reach the floor? How fast is it moving when it hits the floor? At what angle does the ball hit the floor?   (This is an example of a FORWARD problem: we know the initial conditions and are trying to determine something about the object later on.)
Example : Building Height
Hilbun has a flat roof and we'd like to measure it's height. We roll a ball along the roof (horizontally) at some unknown speed vo. Exactly 1.60 sec later, the ball hits the flat ground below after travelling 10 m horizontally.   (a) What was the initial velocity of the ball? (b) How tall is the building? (c) How fast is the ball moving when it hits the ground? (d) At what angle does the ball hit the ground?   (This is an example of a REVERSE problem: we know something about the final or later conditions and are trying to 'reverse engineer' what the initial conditions must have been.)
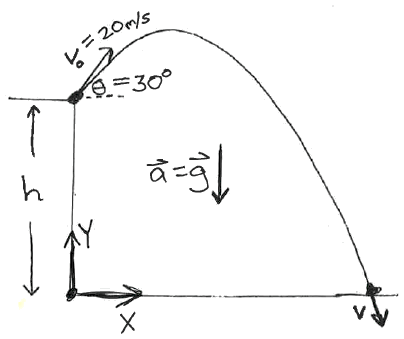
Example : Ball Kicked at an Angle (version 1)
A ball is kicked from the top edge of a 15 m tall building at 20 m/s and at an angle of θ=30o above the horizontal.   How much time does the ball spend in the air? How far from the building will the ball land?     (Forward problem again.)
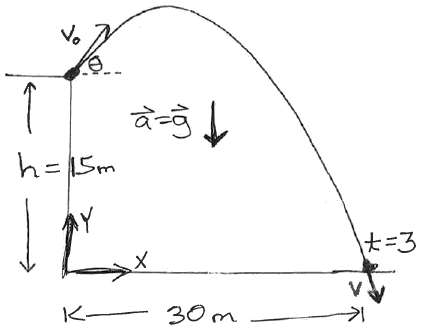
Example : Ball Kicked at an Angle (version 2)
A ball is kicked from the top edge of a 15 m tall building at an unknown velocity and at an unknown angle.   Exactly 3 seconds later, it lands 30 m from the building.   Determine the velocity at which it was launched. (Velocity is a vector, so we're looking for it's magnitude and direction.)     (Reverse problem this time.)
If the acceleration of an object is constant, it's motion is constrained to fit our equations of motion. We may have fragments of information, scattered between the initial and final positions (a velocity here, a time there, ...), so we may have to take different paths through the equations of motion depending on the scenario, but the same equations apply.