Chapter 03 : Kinematics in 2 and 3 Dimensions; Vectors

 

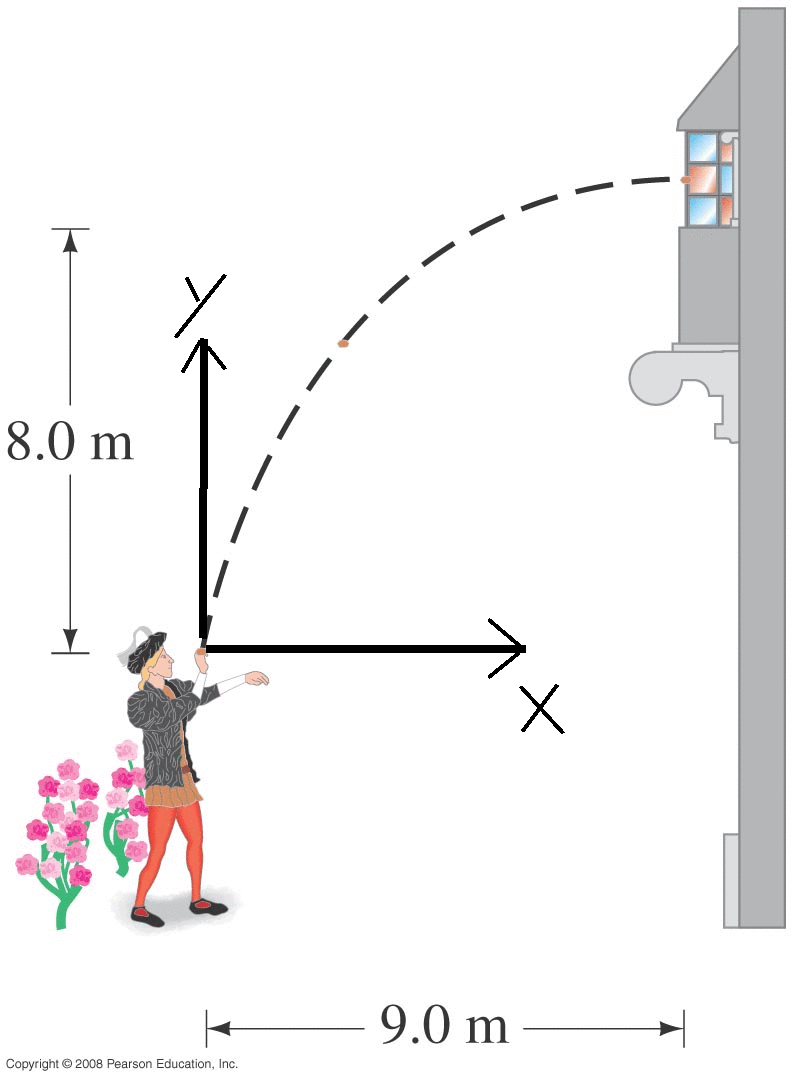
Baseball Landing on Roof
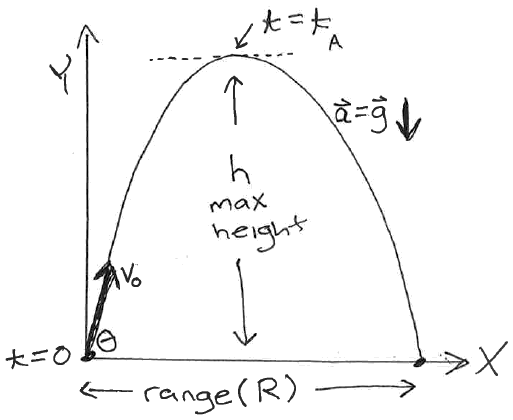
Suppose we hit a baseball such that it leaves the bat at a speed of 27.0 m/s at an angle of 45o. When hit, the ball is 1.0 m above the ground.
Some time later, it lands on the rooftop of a nearby building at a point that is 13.0 m above the ground level. What horizontal distance did the ball travel? How long was it in the air? What maximum height did it reach? How fast is it moving when it hits the roof?
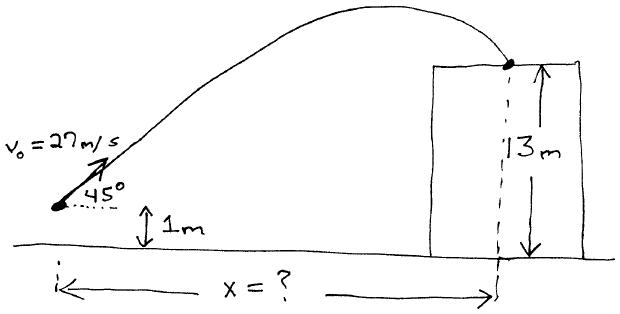
(Be careful here: the ball passes through y=13 on the way up before landing at that same height on the way down, a little later. How can we sort out which solution is correct?)

 

Anvil 'Toss' (Version 1)
There is a group of people who launch anvils into the air using high explosives. The claim in one video is that the anvil reached a height of 200 ft. Given all the dust involved, actually measuring the height would be difficult, so they actually infer the height by measuring the time from when the anvil is launched until it lands on the ground. Suppose this anvil was in the air for 8 seconds and landed at the same spot it was launched from (i.e. it's only moving vertically up and down). Determine the anvil's launch speed and maximum height reached.   Video 1 (see about 1:25) Video 2 (short) (Search for 'anvil toss' or 'anvil firing' for more.)
Anvil 'Toss' (Version 2)
Suppose another anvil is also in the air for the same 8 seconds, but lands 20 m away from where it was launched?   Determine the anvil's launch speed and maximum height reached.

 

Specialized Projectile Motion Equations (Object launched at origin at some speed and angle)
Here we will derive some special-purpose equations that we can apply for certain types of motion, specifically for trajectories where the starting and ending points are at the same elevation. Coordinate System: Origin at launch point +X pointing towards where the object will land +Y vertically upward Acceleration: \( \vec{a}=\vec{g} \) so with this coordinate choice: ax=0 ay=-g=-9.8 m/s2

 

Example: World War 2 Battleship
The US 'Colorado-class' battleships used during World War II fired shells at 2600 ft/s at a maximum angle above the horizon of 30o. What would the projectile range be? How long is the projectile in the air? What maximum height did the projectile reach? If they could have launched at a 45o angle, what would the new range be?
How valid is this calculation? Assuming the Earth is a perfect sphere and your eye is 'h' meters meters above the surface, how far away (in km) is the horizon? \( d \approx \sqrt{12.75h} \) Given a 12 meter high deck, this yields roughly 12 km. Our result above was much larger than that, meaning we need to account for the Earth not being flat!   This led to some of the earliest mechanical computers. The gadget on the right (the Mark I Fire Control Computer, c.a. 1944) weighed around 3000 pounds.

 

Example: Archery

Suppose we fire an arrow at a backyard archery target. (Assume the arrow here is fired at exactly the same height as the bullseye.) First, the arrow is fired horizontally at the target. If the target is 16 m away, we observe that the arrow hits 78.4 cm below the bullseye. How fast was the arrow moving when initially fired?   In order to hit the bullseye, we'll need to aim the arrow up at some angle relative to the horizontal. Assuming it's fired at the same speed as before: Determine the launch angle needed for the arrow to hit the bullseye. Approximately what is the maximum range of the arrow? How long would it be in flight?

 

Example where the Specialized Equations aren't ideal

(HW 3.52) Romeo is throwing pebbles gently up to Juliet's window and he wants the pebbles to hit the window with only a horizontal component of velocity. He is standing at the edge of a rose garden 8.0 m below her window and 9.0 m from the base of the wall (see figure). How fast are the pebbles going when they hit her window? At what speed and angle were the pebbled 'launched'? If the building weren't there, the rock would continue flying along this parabola and land on the ground. What we're seeing is basically the first half of the parabola in our super-specialized equations of motion, where the object has a range of R=18 meters, and an apogee height of h=8 meters. Try using the R and h equations of motion to solve this. (You'll need to remember some trig identities!) Try using the more general equations of motion. (What do we know about vy when the pebble hits the window?)

 

Football Throw
A quarterback throws the ball to a location where the receiver will be located some (brief) time later. For a particular throw, suppose the ball needs to arrive at a location 30 m from where it was thrown, and needs to arrive at that location 1.5 sec after being thrown. (Assume the ball is thrown and caught at the same elevation.) At what speed and angle must the ball be thrown?	Lamar Jackson, Baltimore Ravens

 

Snake River Canyon Jump

On 16 September 2016, stuntman Eddie Braun successfully jumped a motorcycle (more like a rocket bike) across the 1400-foot-wide chasm of the Snake River Canyon (a feat initially but unsuccessfully attempted by Evel Knievel on 8 September 1974). The news photograph shows a launch angle of about 54o (instead of the optimal 45o, so what must the initial launch speed have been? Another article claimed the bike reached a maximum height of 2000 ft. What initial launch speed does that imply? A third article claimed the bike reached a maximum speed of 400 MPH. What initial launch speed does that imply?   These all give very different values for vo because in reality this is not simple projectile motion. The rocket continued to fire for a while when the bike was 'launched', meaning the acceleration here is not simply g, so unfortunately we can't really use any of our equations to analyze this scenario. :-(

 

Clown Gun Stunt

We have been asked to evaluate the feasibility of doing a spectacular stunt during half-time at the Egg Bowl game. Based on the 'clown gun' stunt sometimes seen at carnivals or circuses, a person will be launched from a large cannon and fly through the air across the entire length of the field, landing 'safely' in a large net.   The launch and landing points are exactly 100 m apart. The volunteer will accelerate from rest to the required launch speed over a distance of 4 meters in the barrel of the cannon. A fit human can reasonably withstand an acceleration of 5 to 10 g's for brief periods.

(a) What is the 'best' launch angle? (b) What launch speed at B is needed to achieve this? (c) What acceleration will the person have to undergo from A to B to reach the required launch speed?   Can we pull this off safely?