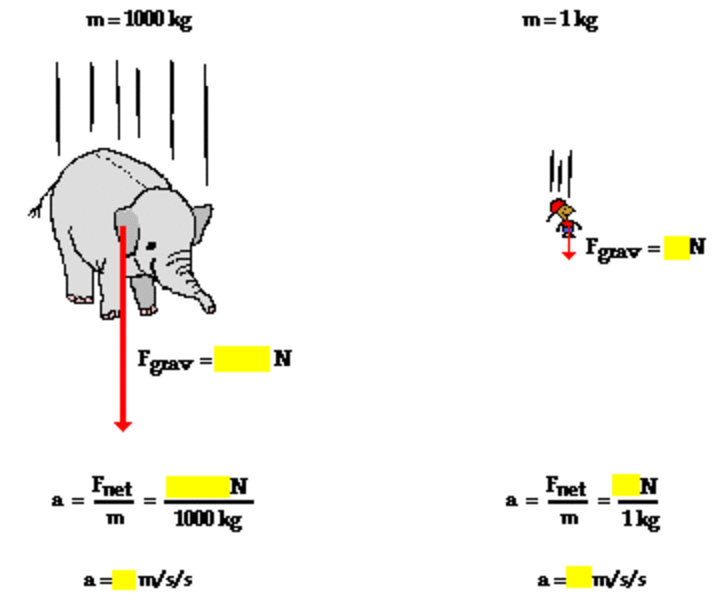
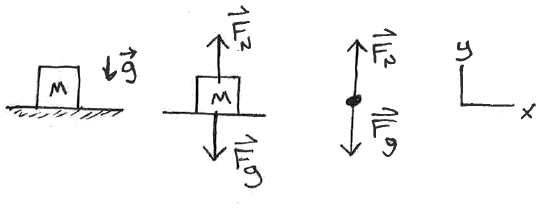
Force vs Acceleration
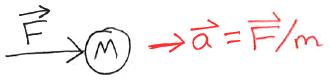
Units:
[acceleration units] = [force units]/[mass]
[force units] = [mass]*[acceleration units]
MKS : kg·m/s2 = Newtons (N)
English units : 1 pound (lb) = 4.44822 N or 1 N = 0.2248 lb
CGS : g·cm/s2 = dyne (N)
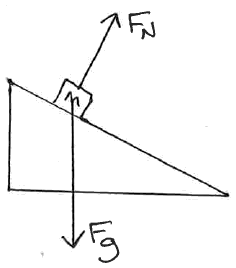
Multiple Forces
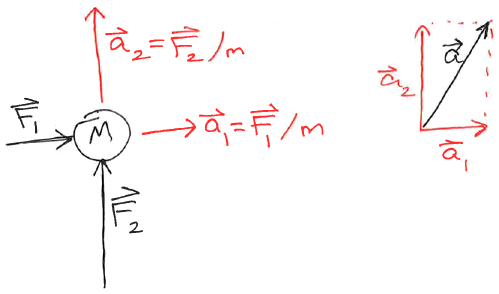
\[ \sum \vec{F}_i = m\vec{a} \]
Useful to determine an unknown force.
A single force can be replaced with other forces (aligned with your coordinate system) that add up to that original force.
Newton's Laws
First Law
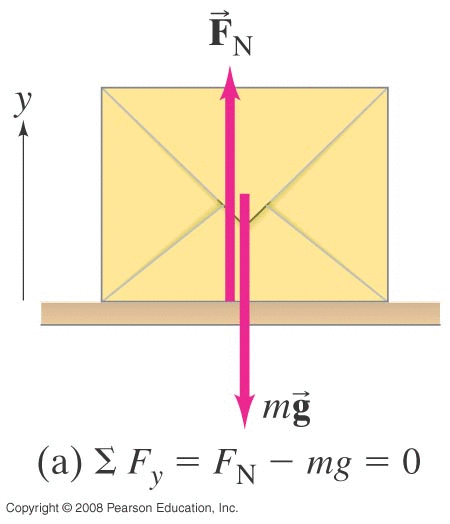
If there is no net force on an object, it will continue to move with a constant velocity (which could be zero but doesn't have to be).
\[ \sum \vec{F}_i = 0 \hspace{1em} implies \hspace{1em} \vec{a}=0 \]
\[ \vec{a}=0 \hspace{1em} implies \hspace{1em} \sum \vec{F}_i = 0 \]
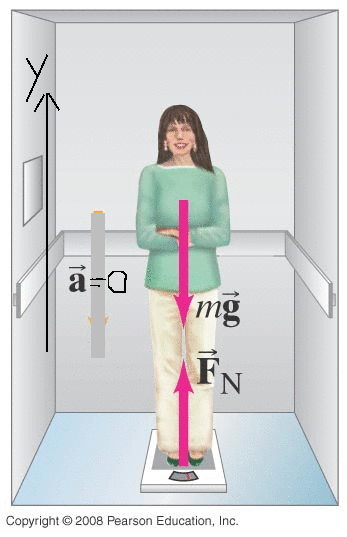
Second Law
If there is a net force on an object that it will cause that object to accelerate according to \( \sum \vec{F}_i = m\vec{a} \)
Note the picky wording there: The forces acting on an object are what produce the acceleration of that object.
Other forces may be present elsewhere, and may indirectly work their way onto the object, but ultimately it's the forces acting directly on the object that are all it `knows' about.
(Will become important when multiple objects are involved.)

Third Law
All forces are interaction forces. If object A exerts a force on B, then B exerts an equal and opposite force on A: same magnitude, opposite direction.