Chapter 04 : Newton's Laws

 

 

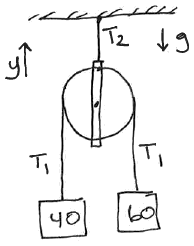
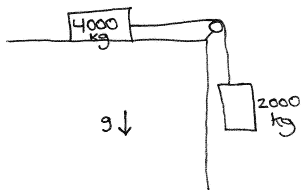
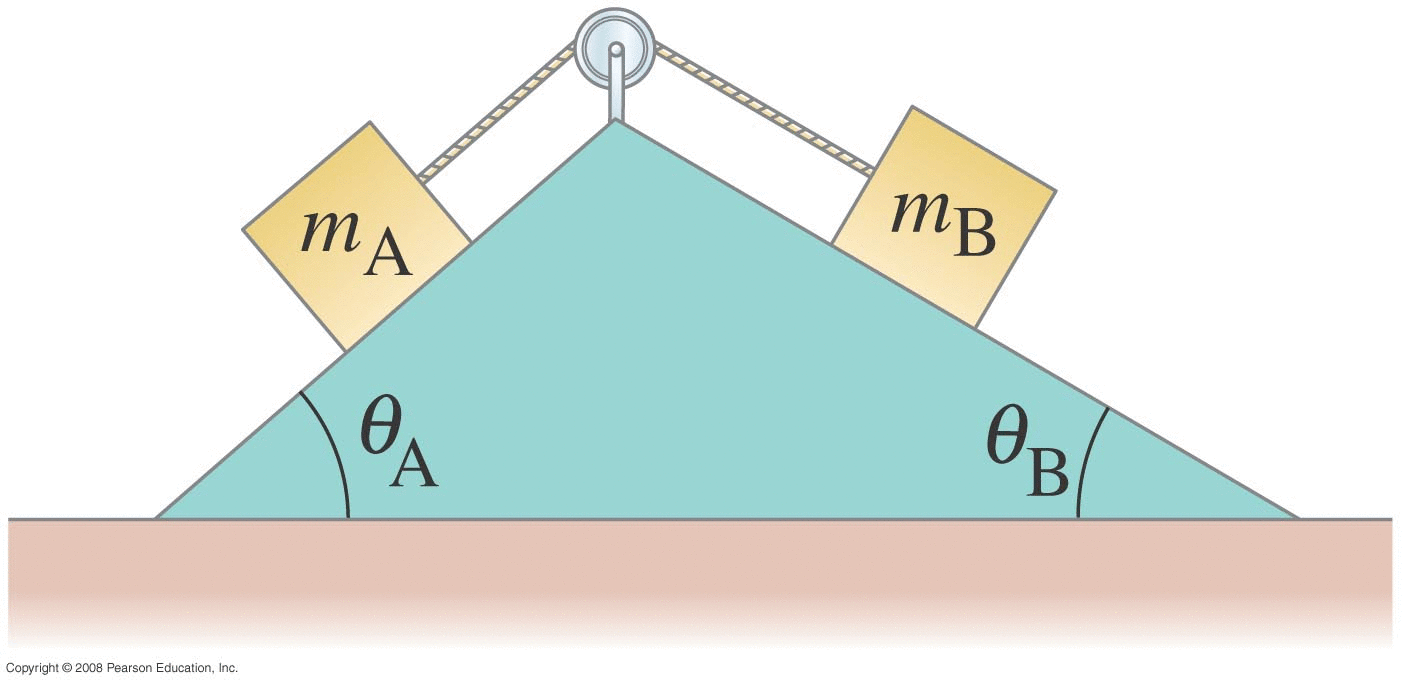
Connected Sleds

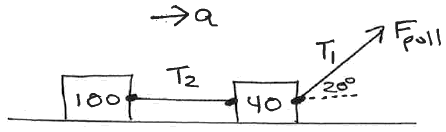
Suppose we have two sleds being pulled across flat, horizontal (frictionless) ground.

The sleds are connected together with a short horizontal piece of rope, and the front sled is being pulled with a rope that has some amount of pulling force applied to it at the 20o shown in the figure.

The sleds are observed to be accelerating to the right at 0.5 m/s2.

 

  • What must the pulling force be?

  • How much tension is in the rope connecting the two sleds?

 

 

 

Simple Pulley

 

A 40 kg box is hanging from a cable that runs over a pulley (which is attached to the ceiling).

  • How much force is the person exerting downward on the right to be able to hold the box in place?

  • How much tension is in the cable connecting the pulley to the ceiling?

 

 

Double Pulley

In the previous example, we didn't really gain any mechnical advantage: we had to pull on the box with a force equal to it's full weight. In addition, the pulley ended up exerting a force on the ceiling equal to twice the weight of the box.

Suppose we add a second pulley as shown in this figure. How much force do we need to exert now, and determine the tensions in all the cables present. (The mass of the box remains 40 kg.)

  • How much force is the person exerting downward on the right to be able to hold the box in place?

  • How much tension is in the cable connecting the pulley to the ceiling?

 

 

More Complicated Pulley Systems

 

 

"Atwood Machine"

Let's expand on the first pulley problem and have a second box hanging on the right, instead of a person pulling on the cable.

Let's make this second box heavier so that the system is no longer in equilibrium and will accelerate.

 

Here, we have our original 40 kg box on the left, and now we also have a 60 kg box on the right.

 

  • Determine the tensions present and the acceleration of the boxes.

 

NOTE: I'll use these examples to illustrate the side-effects of what coordinate system(s) you choose.

Newton's Laws apply separately to each object, so you can (and usually should) use a different coordinate system for each object.

 

 

"Jurassic Park" (version 1)

In one of the early Jurassic Park movies, a dinosaur has pushed half of a connected trailer over the edge of a cliff.

Suppose the two objects are initially at rest and we have no friction yet (we'll look at a more `realistic' version of this problem in the next chapter that does include friction).

 

  • Determine the acceleration of the two objects.

  • How much tension is in the cable?

 

 

Connected Objects on Ramps

 

This problem was inspired by some roofers working on my house a few years ago. Two roofers would be on opposite sides of the peak with a rope connecting them for safety.

In this figure we have:

  • Left side: 40 kg box on a 60o ramp.

  • Right side: 60 kg box on a 30o ramp.

 

  • Determine the acceleration of the boxes.