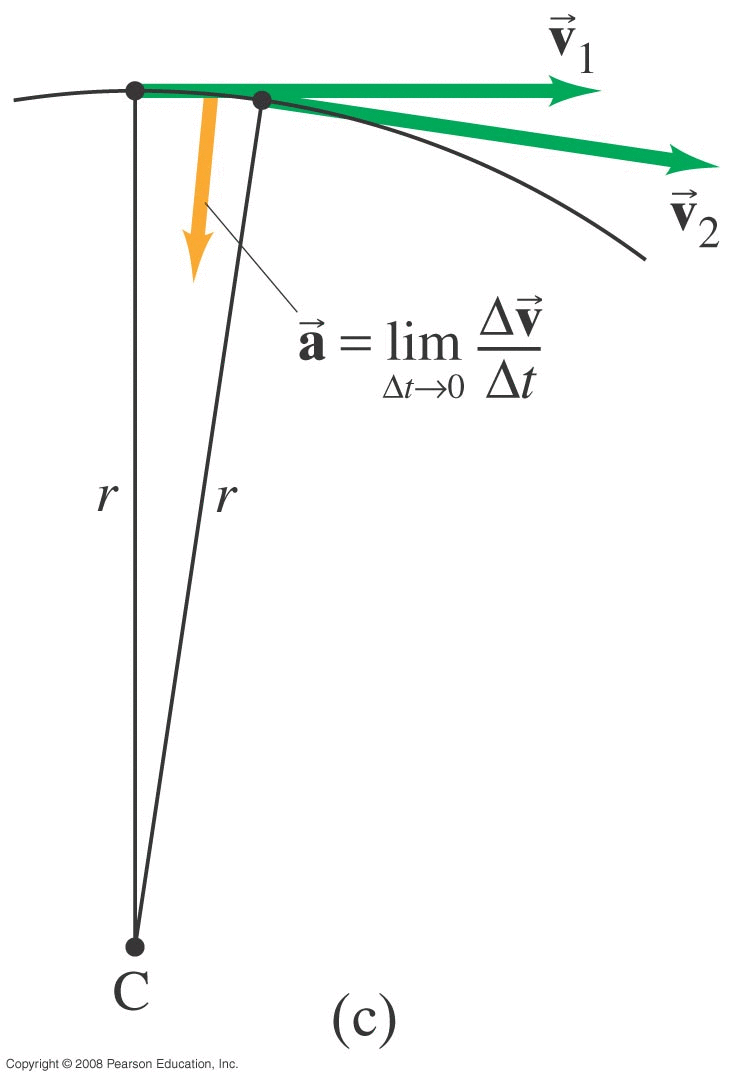
Review : Test 2 Practice problem HW04-15
A 14 kg bucket is being lowered vertically by a rope in which there is 132 N of tension.
(a) What is the acceleration of the bucket? (Up or down?)
Suppose the mass of the bucket is 12 kg and the tension is the same 132 N.
(b) What is the acceleration of the bucket? (Up or down?)
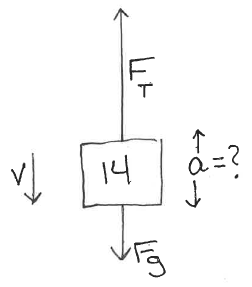
(Sketch what v(t) looks like in each case.)
Remember: velocity and acceleration (a=dv/dt) are two completely different things.
The sign of one tells you nothing about the sign of the other.
Review : Test 2 Practice problem HW05-YY
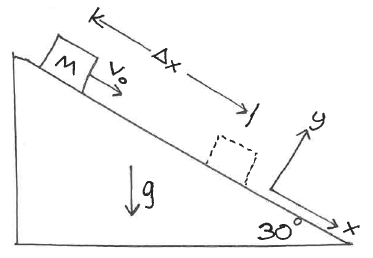
A 10 kg box is sliding down a rough 30o incline as shown in the figure. In the upper position, the box is sliding down the incline at 50 cm/s but we observe that the box is slowing down and comes to a stop after sliding 50 cm along the ramp.
(a) What must the kinetic coefficient of friction be?
Review : Test 2 Practice problem HW05-ZZ
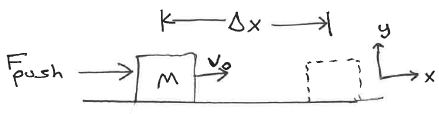
A box of unknown mass M is sliding across the floor to the right at 1.5 m/s and is being pushed with a constant force of Fpush=200 N.
The (flat, horizontal) floor is rough, with a coefficient of kinetic friction of μk=0.6 and we observe that the box is slowing down, coming to a stop after travelling 50 cm.
(a) What must the mass of the box be?