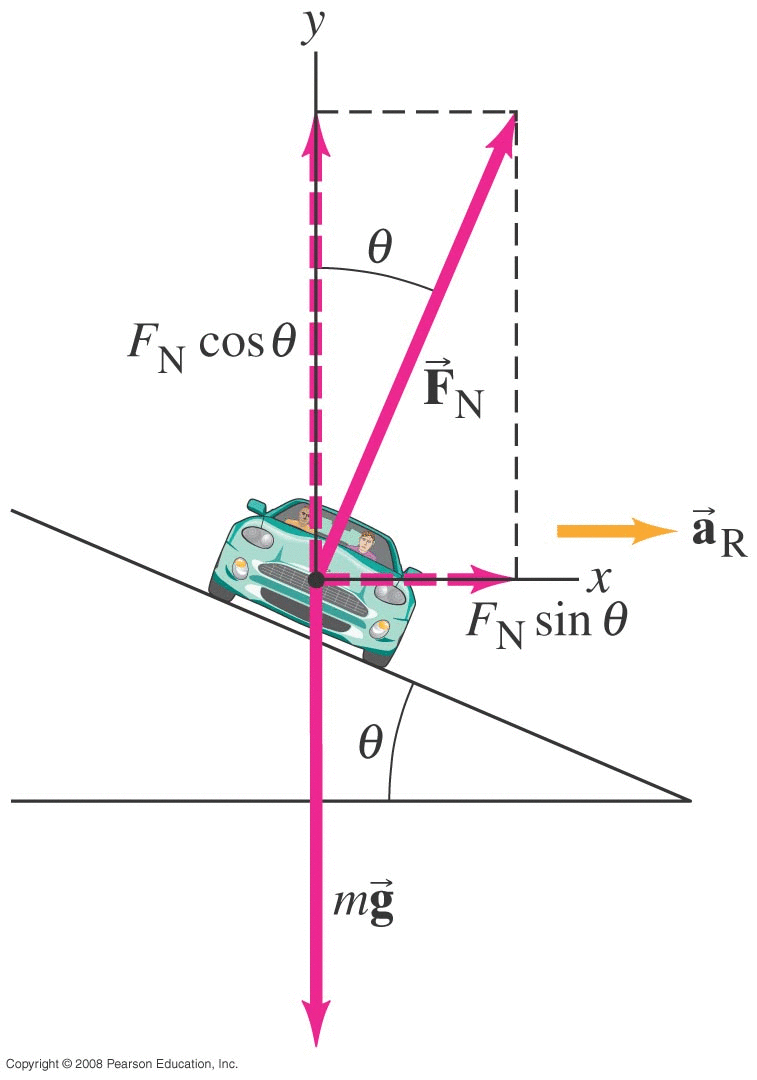
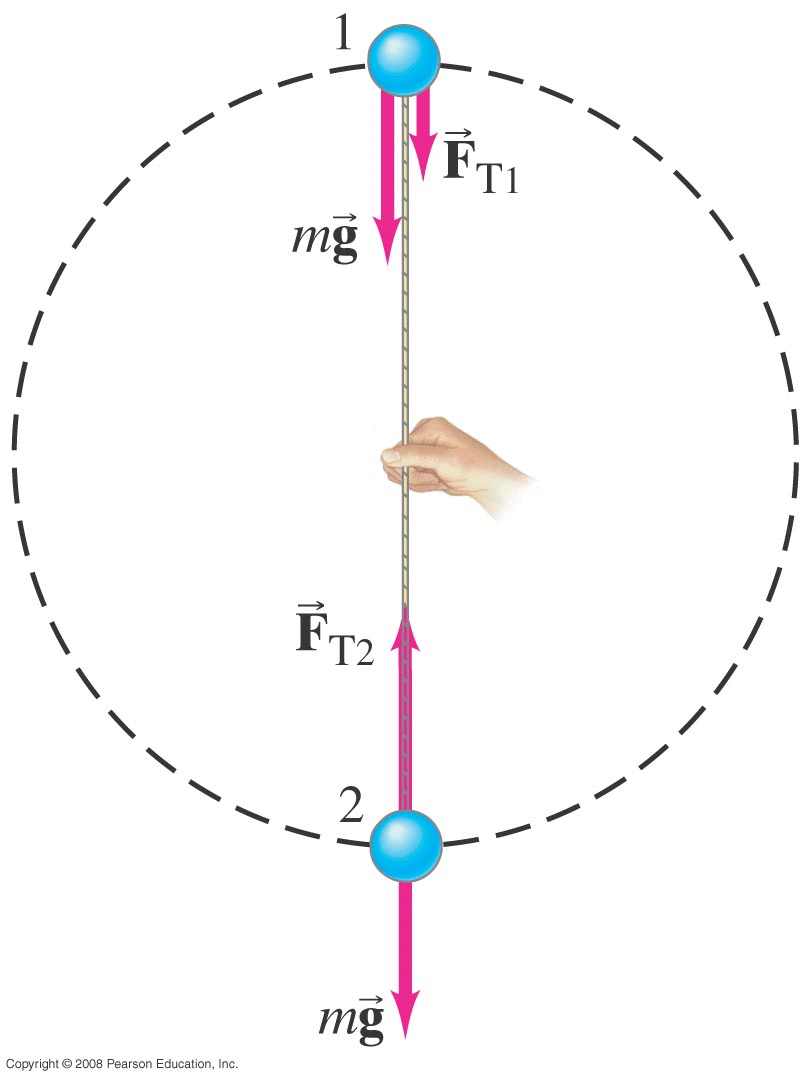
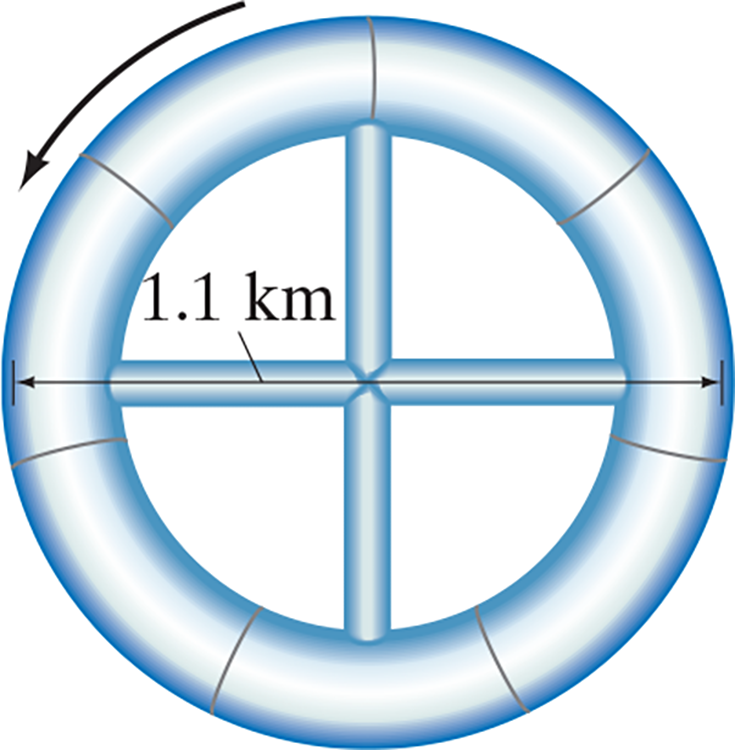
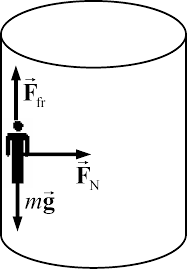
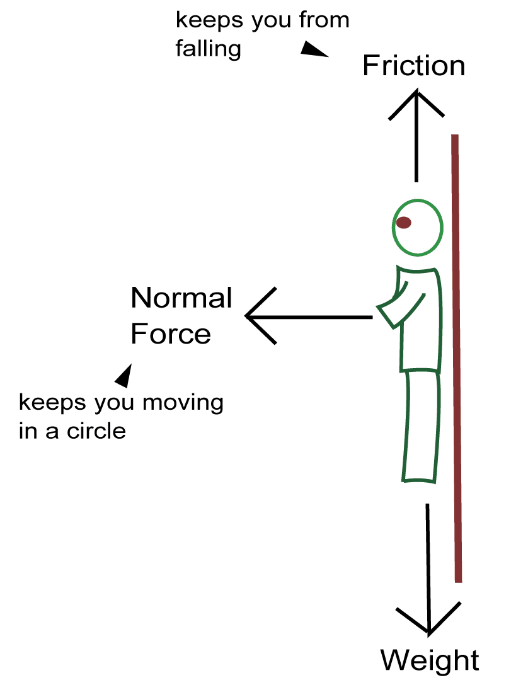
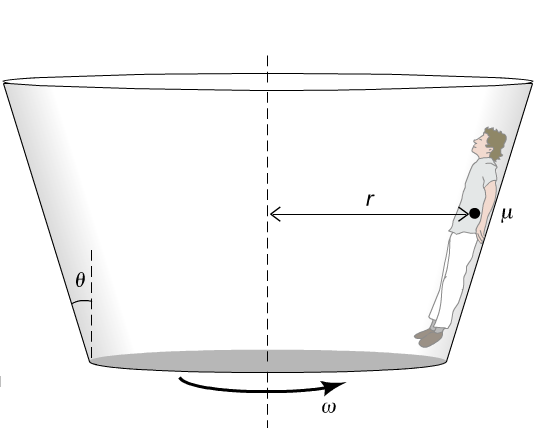
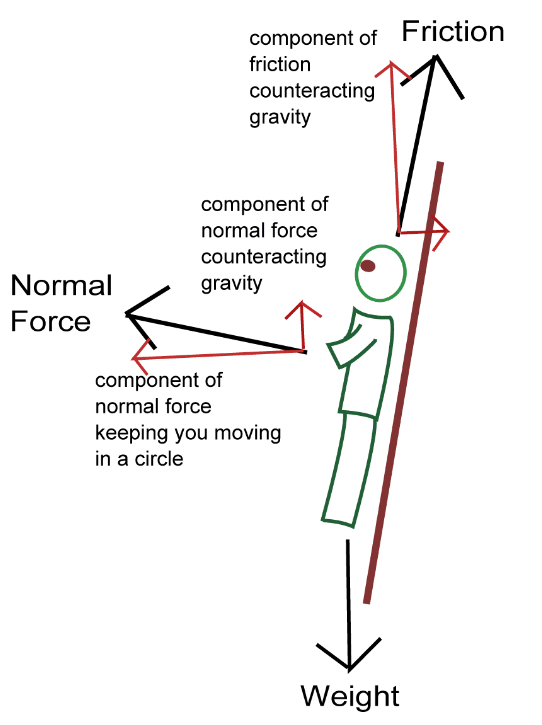
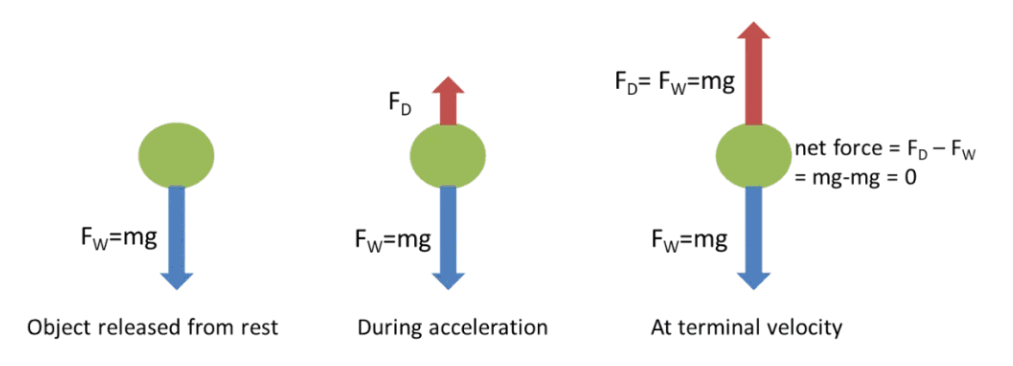
Uniform Circular Motion : Summary

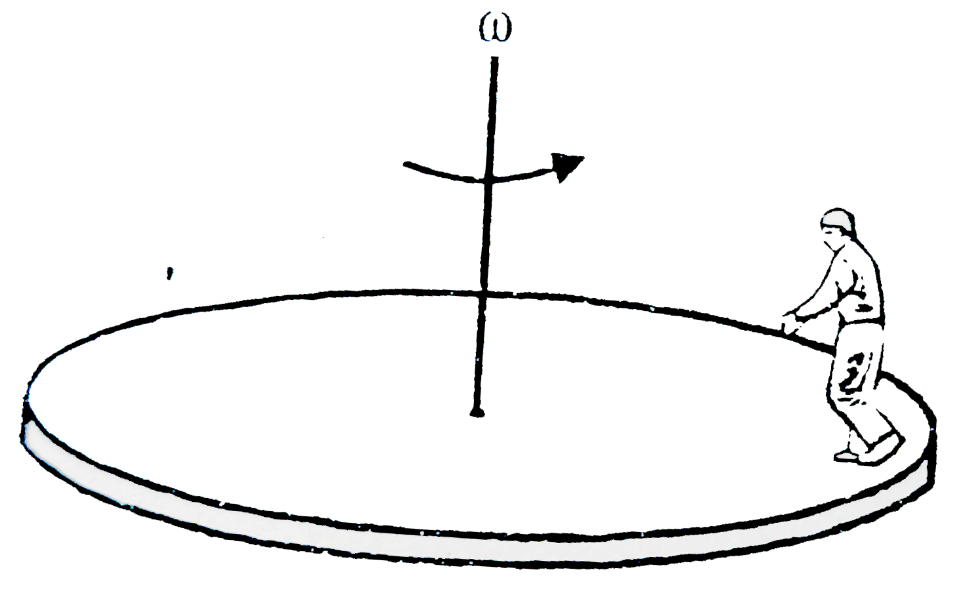
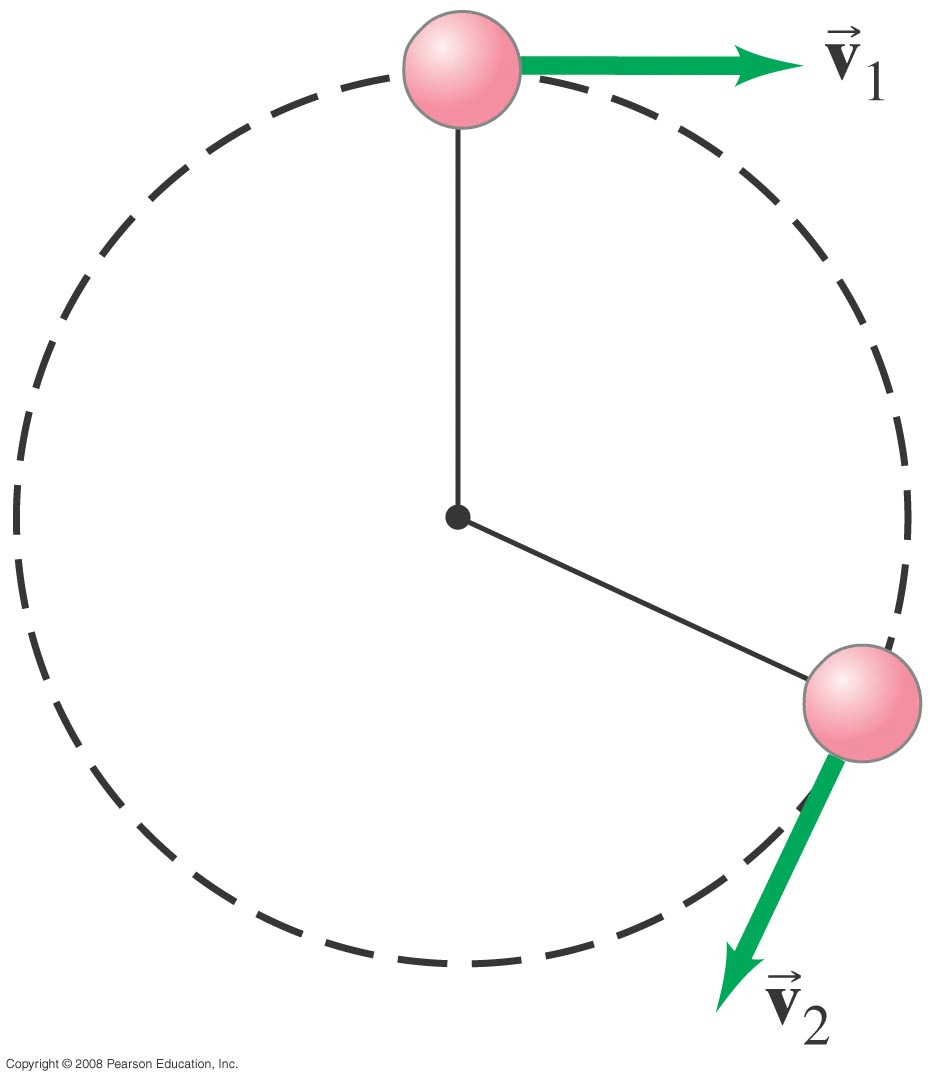
T : PERIOD : the time per rotation (or cycle or revolution or ...) f : FREQUENCY : rotations per time, so f=1/T UNITS: ideally rotations per second : s-1 also called Hertz (Hz) Commonly encountered unit: RPM (revolutions per minute) Constant speed; object is travelling around a circle of radius r so: v=(2πr)/T = 2πrf T = 2πr/v   Radial Acceleration    Magnitude: ar = v2/r    Direction: radially inward

 

Example: SpinLaunch
Goal: spin a satellite fast enough to avoid needing the first stage of the rockets normally used.   (Last test flight seems to have been in 2022...)
Actual Test Facility (New Mexico)	Eventual Goal

 

Example: Merry-Go-Round
A Merry-go-Round takes 4 seconds to make one complete rotation.   If a person is standing on the outer edge of the MGR, 4 m away from the center, what radial acceleration do they have? What must be the coefficient of static friction between their shoes and the floor of the MGR so that the person doesn't slip?

 

Example: Unbanked Turn
A flat highway exit ramp has a radius of curvature of 60 m. What speed limit(s) should be posted (one for dry conditions, one for wet)? Assume: μs = 0.8 for rubber against dry concrete μs = 0.6 for wet conditions. Speed Limits (right at the limit): Dry: ____________ miles/hour Wet: ____________ miles/hour Speed Limits (more likely posted): Dry: ____________ miles/hour Wet: ____________ miles/hour

 

Example: Banked Turn
Suppose we want to design an offramp with a very tight radius of curvature that works no matter the road conditions - even if it's covered with slippery oil and there's no friction present at all. How is the car speed v related to the banking angle? (I.e. how fast would the car need to travel so that it will stay on the road and not slide up or down along the banked surface?) (Race car track turns are usually banked like this, although not to the extremes we'll see in this example.)   If the track is banked at a 30o angle and has a radius of curvature of 60 m, what speed does our analysis imply? What angle would be needed if v = 100 MPH (about 45 m/s; a typical speed in turns at race tracks)? The tracks in the figures below aren't remotely that steep. What else is keeping the cars from flying off the tracks?

 

Example: Mythbuster's Swingset Stunt
In an old episode, they tried to have a person swing around in a complete circle on a swingset. (They were unsuccessful, so in true Mythbusters fashion, they ended up attaching rockets to the back of a dummy to get it moving fast enough to go around in a complete circle.) Suppose M=50 kg and r=2 m here. How fast does the object need to be moving at the top of the circle in order to actually keep moving along the circle? (If it's moving too slowly, the chain will just go slack.) When the object swings past the bottom of the circular path, it will be moving \( \sqrt{5} \)   (about 2.24) times faster than it was at the top (we'll see where that comes from in a later chapter). How much tension is in the chain(s) at this point?

 

Example: Artificial Gravity
HW05-54 : A proposed space-station consists of a circular tube that will rotate about its center (like a tubular bicycle tire). The circle formed by the outer edge of the tube has a diameter of 1.1 km. What must be the rotation speed (in revolutions per day if an effect nearly equal to gravity at the surface of the earth, 0.9 g, is to be felt by astronauts standing inside? (For this to happen, basically they'll need to stand so their feet are planted on the inner surface of the outer edge of the tube. That normal force will 'feel' like the same normal force they'd feel if their feet were on the Earth.)
Cutaway view showing curvature to scale

 

Example: Carnival Ride

 

Resistive Forces
Objects moving through liquids or gasses (like air) don't actually pass through those materials: the medium has to be pushed out of the way temporarily which requires a certain amount of force. From Newton's third law, the object feels an equal and opposite force resisting it's motion, referred to as a DRAG FORCE.
This drag force increases as the speed of the object increases (in a very complex way) but that means that eventually the object may reach a speed where this resistive drag force matches the other forces in the scenario. At that point, Σ F = 0 so a=0. That final constant speed is commonly called the terminal velocity.
Velocity v(t)	Acceleration a(t)
Skydiver
Person falling through air without a parachute: 'belly down' orientation: vT ≈ 120 mph Head or feet first: vT ≈ 150 to 180 mph With parachute: much lower speed: vT ≈ 15 miles/hour

 

Common Approximations
Low speed: LAMINAR flow Modelled as: F=-bv (solvable differential equation)	High speed: TURBULENT flow Modelled as: F=-Cv2 (solved numerically; or just use a wind tunnel!)