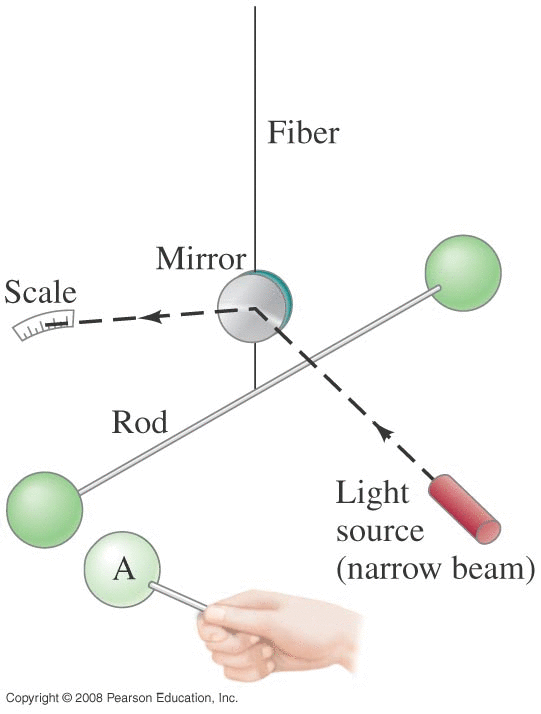
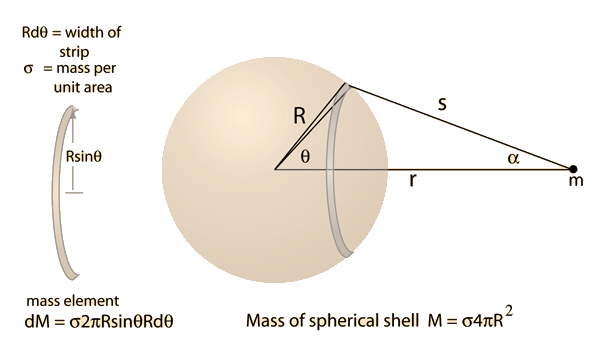
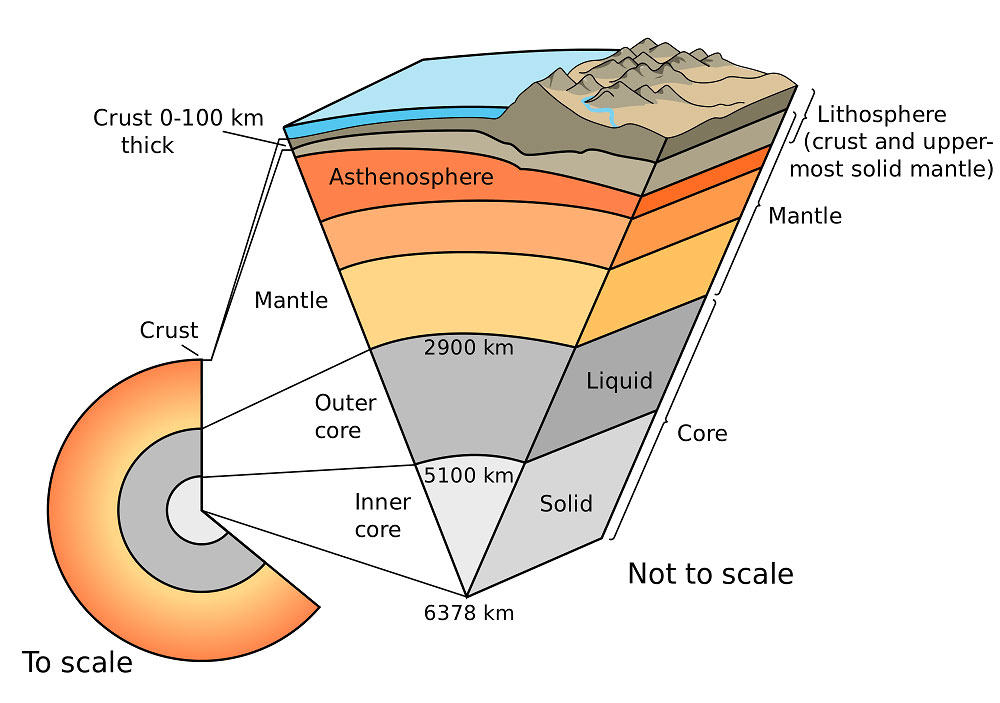
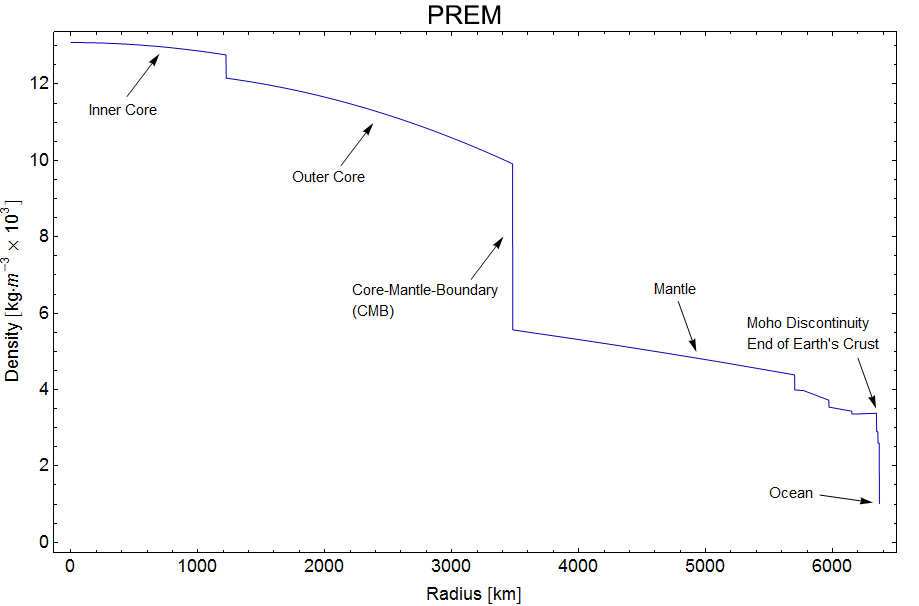
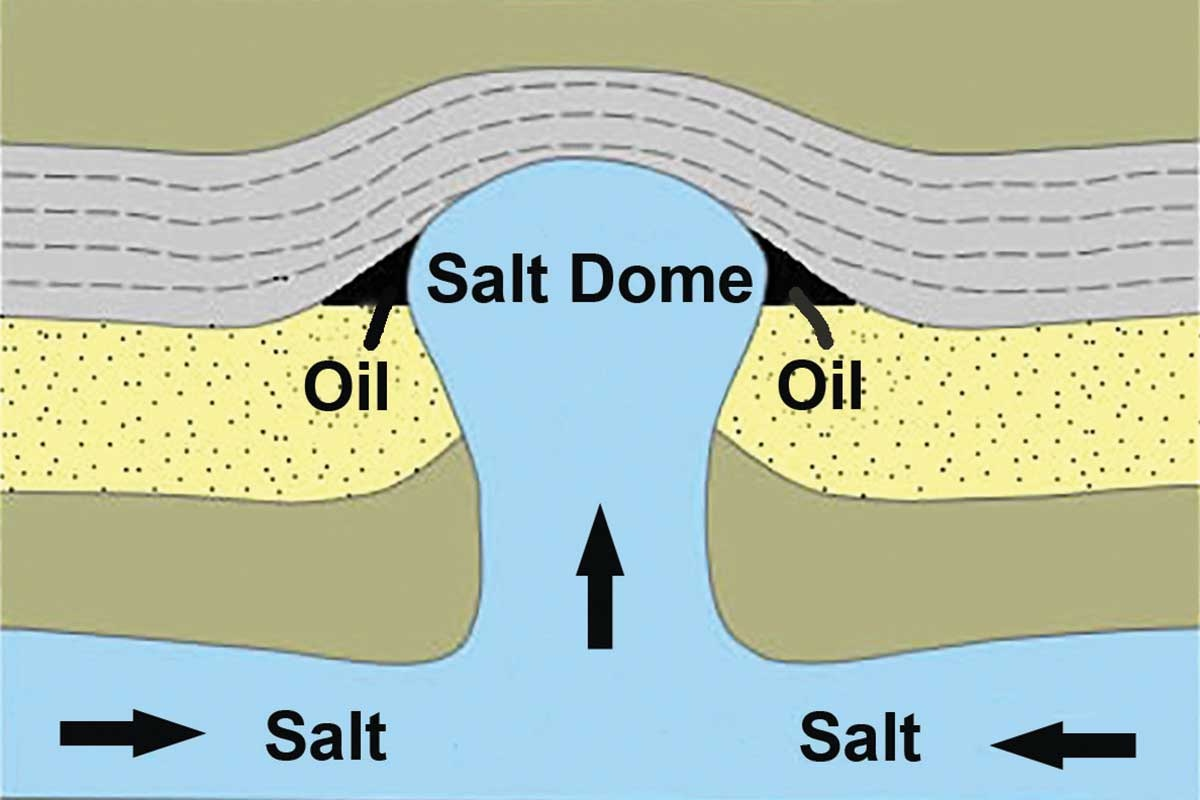
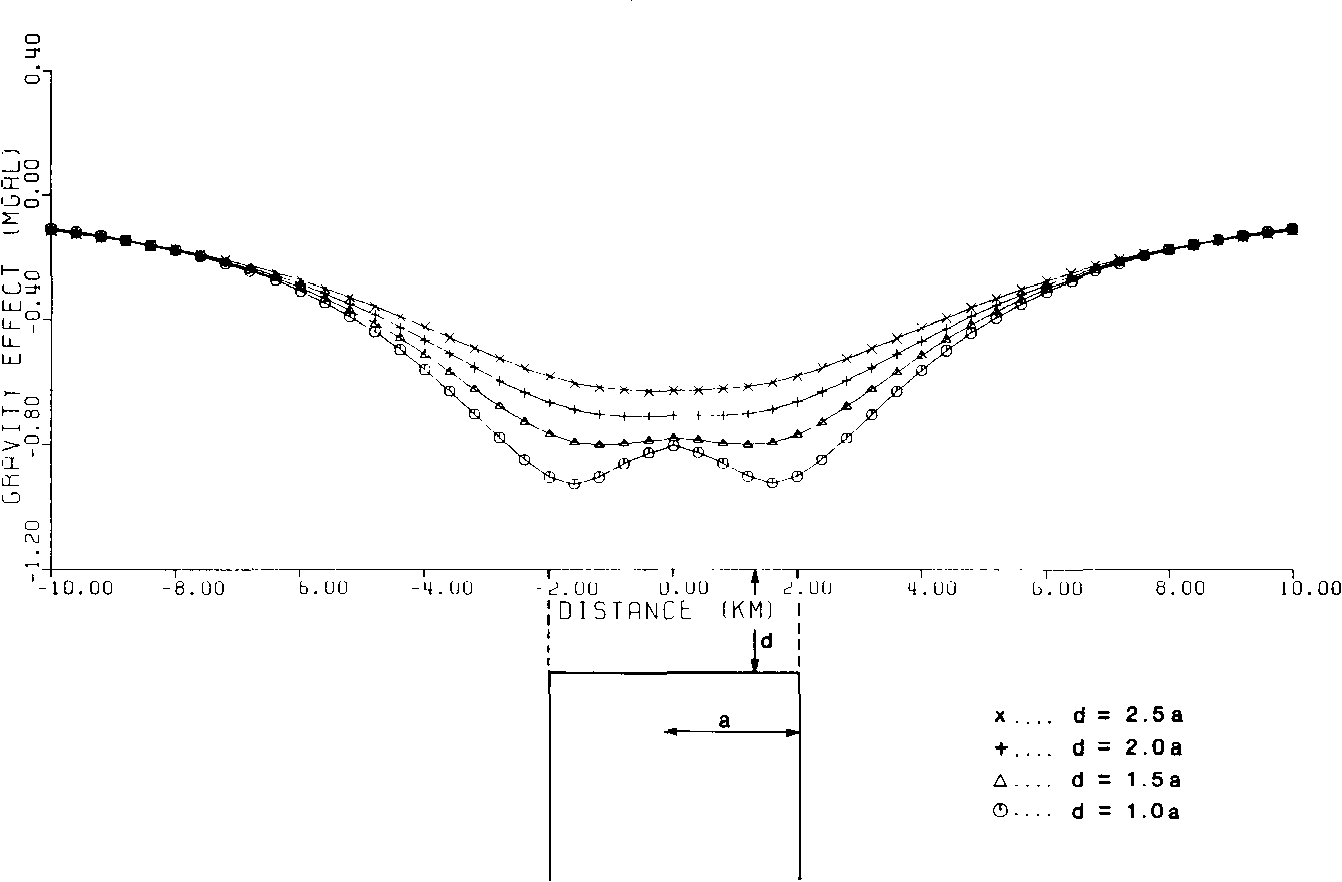
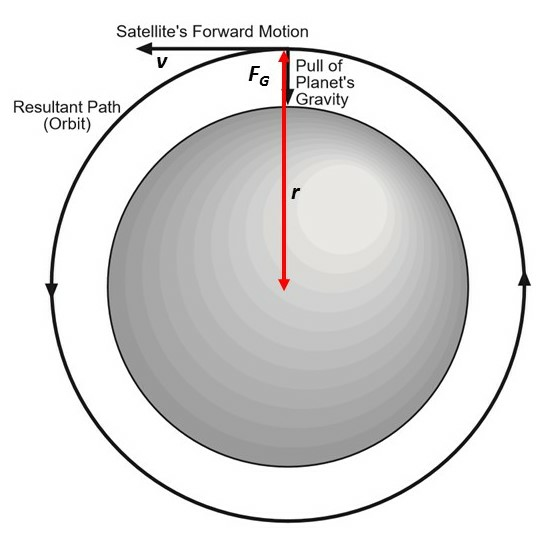
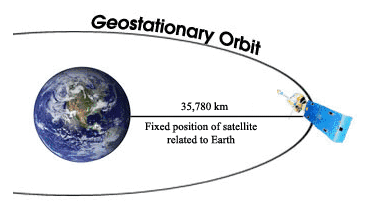
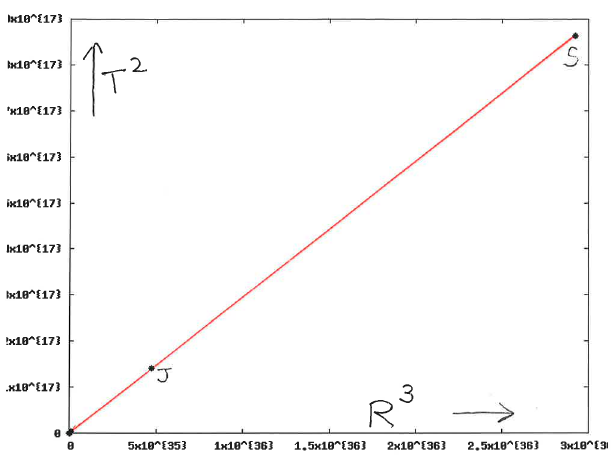
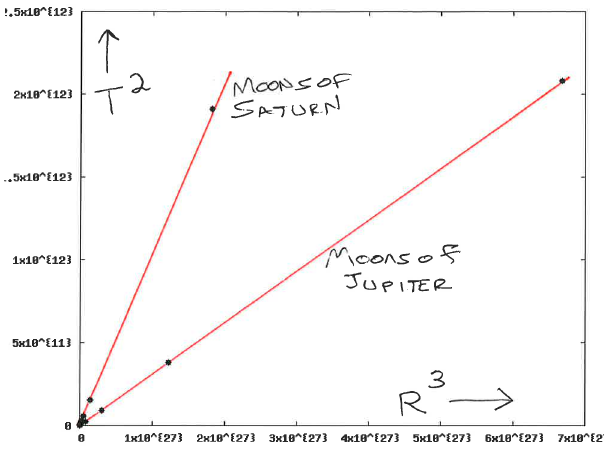
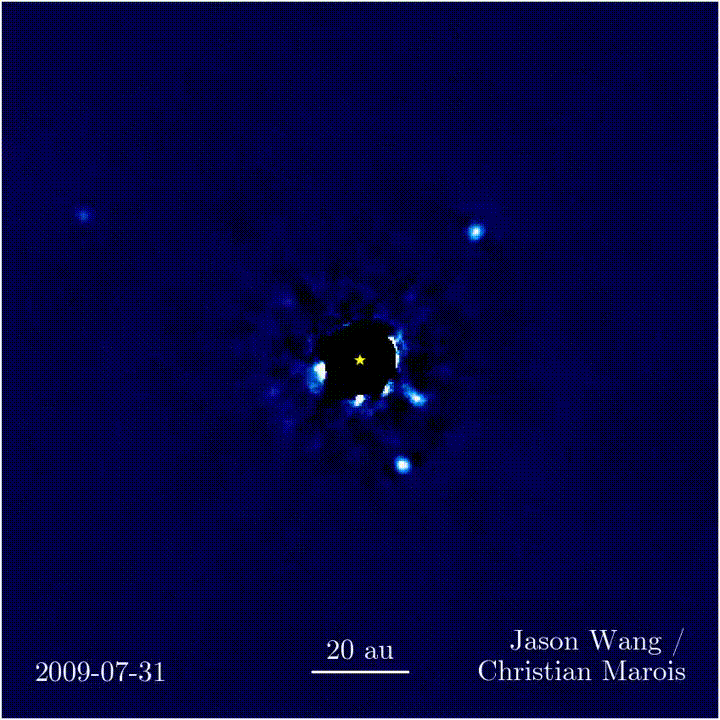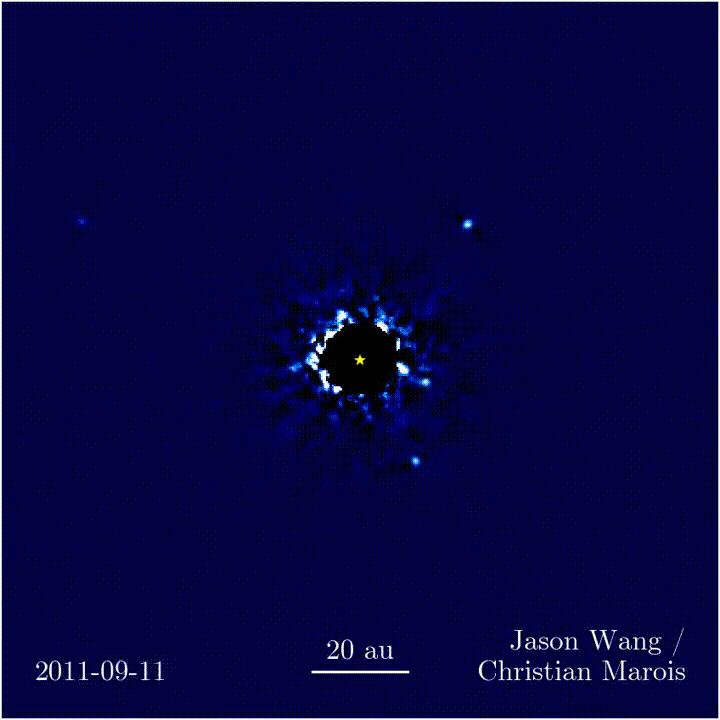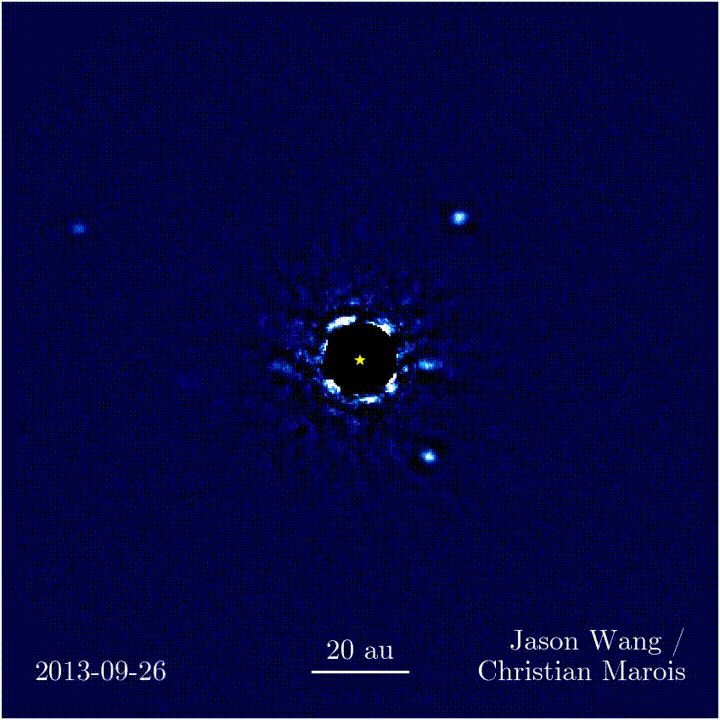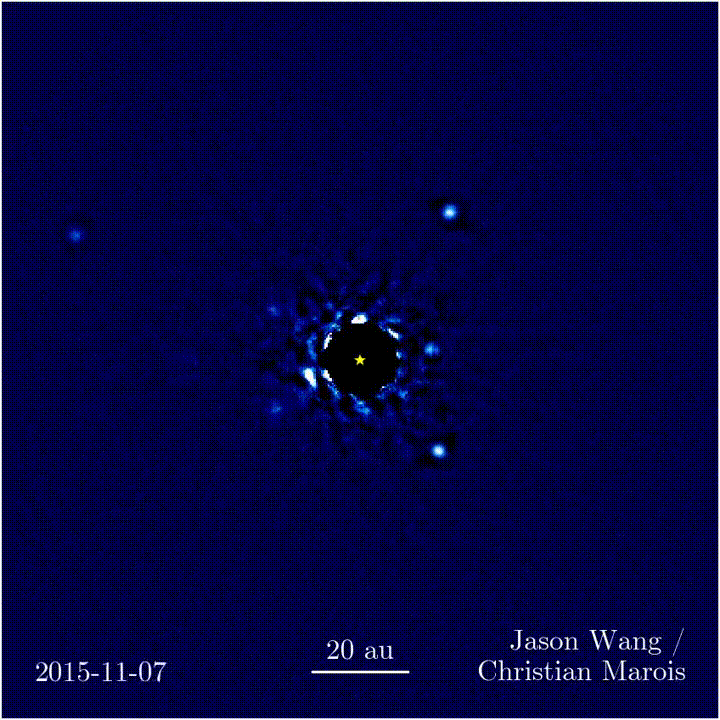
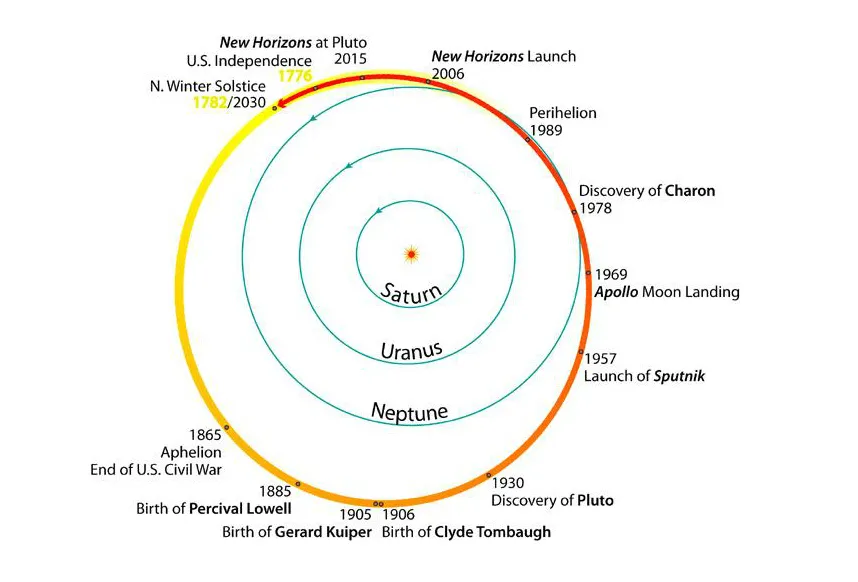
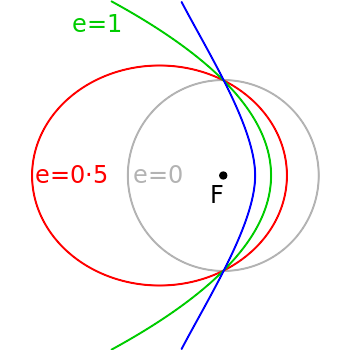
Newton's Universal Law of Gravity
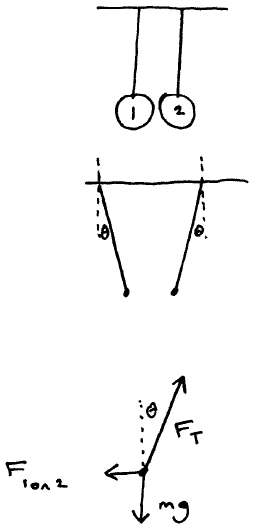
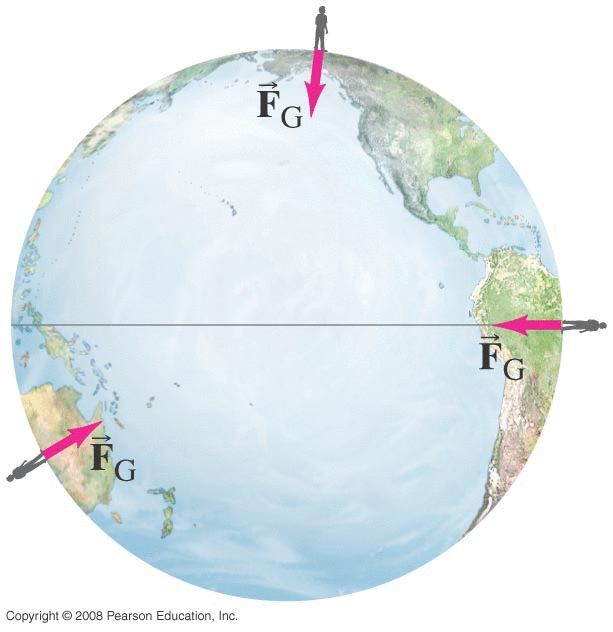
Newton (1687) proposed: (point) masses attract with a force proportional to each of their masses and inversely proportional to the distance between them: Magnitude: \[ F_G = G \frac{ m_1 m_2 }{r^2} \]   Direction: attractive (always) Notation:     \( \vec{F}_{21} \) is force on 2 due to 1     \( \vec{F}_{12} \) is force on 1 due to 2     (equal and opposite forces)

 

Determining G : the Cavendish Experiment (1798)
Two masses in the form of a dumbell hanging from a thin wire. Another mass is brought near. The gravitational force causes the wire to twist; observing the effect amplitifed by narrow beam light source and mirror attached to the wire.     Latest result:   \[ G = 6.6743 \times 10^{-11} ~N \cdot m^2/kg^2 \]

 

Non-point Masses
Calculus : break object(s) into infinite number of infinitesimal point masses and 'do the (vector) integral'.   Convenient subset : IF the objects are spherical and have a constant density (or as long as the density only depends on r, making the objects spherically symmetric: THEN mathematically they act as point masses with all their mass located at their centers. (Most stars, planets, and large moons qualify.)
Earth cross-section	Earth density profile (approximate)

 

Example: Bowling Balls on Wires

Two 5 kg bowling balls are hanging from 1 meter long wires. The balls each have a diameter of 16 cm and their centers are 17 cm apart (so their surfaces are 1 cm apart at the closest point). What is the gravitational force between them? What angle does each cable make with the vertical? (The wires appear vertical but actually aren't...) How far has each ball moved (relative to vertical)?   Apply Newton's Laws to determine the actual angle.

 

Relating Fg and FG
M = mass of the Earth; m = mass of object Object located at surface so r=R (radius of the earth) \[ F = G \frac{ M m }{R^2} \] Near the surface, we've been approximating this as F=mg, so: \[ g = \frac{ GM }{R^2} \]

 

 

Variation of g
The Earth is not a uniform sphere, so g varies slightly.
UNITS: 1 Gal = 1 cm/s2 = 0.01 m/s2 1 mGal = 0.001 cm/s2 = 0.00001 m/s2
Exploited in oil and gas exploration (among other things):

 

Orbits
Gravity is a radially-inward force, which is just what we need for circular motion. Consider a light object of mass m orbiting a much heavier object of mass M, in a circular path with a radius of r \[ F_r = ma_r \] \[ G\frac{Mm}{r^2} = m\frac{v^2}{r} \] \[ v^2 = GM/r \]
International Space Station
The ISS orbits about 254 miles above the surface of the Earth. Determine its orbit speed and period. Careful: the r needed here is the radius of the circular orbit itself. Radius of the Earth: Re = 6.38 X 106 m Mass of the Earth: Me = 5.972 X 1024 kg Height above surface: h=254 miles → 4.26 X 105 m G = 6.6743 X 10-11 N m2 / kg2 radius of orbit circle: r = h+Re = 6.81 X 106 m v = ?     (ref: 'Gravity' movie, 2013) T = 2 π r / v = ? Satellites that orbit within just a few hundred miles of the Earth's surface are referred to as Low-Earth Orbit (LEO) satellites. This website shows orbits of some of the current large LEO constellations used to provide internet: https://satellitemap.space

 

Geostationary Orbit
The Earth rotates once every (approx) 24 hours, but low-earth-orbit satellites only take just over 90 minutes to do so. They pass overhead quickly. An optimum location for some satellites is an orbit where it takes exactly the same (approx) 24 hours, causing the satellite to appear stationary in the sky.   First, a useful equation: Found earlier: v2 = GM/r Definition: T = 2 π r / v Combine those. Result is: 4 π2 r3 = G M T2
GEOSTATIONARY ORBIT Requires T = 23 hours, 56 min, 4.09 sec = 86164.09 s Result: r = 4.2174 X 107 meters or 42174 km or 26210 miles (all measured from the center of the Earth, so about 22250 miles above the surface). Resulting lag : Old HughesNet geostationary internet provider satellite: signal has to travel from you to the satellite, back to the game/website on Earth; then back up to the satellite; then back to you. Overall at the speed of light would take about 480 ms

 

Determining Mass of Planets, Moons, (other Stars, ...)
Any (relatively) light objects orbiting a (much) heavier object will show that behavior: r3 ∝ T2;   Specifically:   \( T^2 = (\frac{4 \pi^2 }{GM}) r^3 \) Satellites in Earth orbit Planets orbiting the Sun (Light) Moons orbiting (much heavier) planets Observations of the last two (planets around the Sun, and moons around Jupiter) led Newton to the particular form of his gravitational force equation. The mass of the Sun can be determined by using the period and orbit radius of the planets The mass of a planet like Jupiter can be determined using the period and orbit radius of the (many) moons orbiting the planet The mass of other stars can be determined using the period and orbits of planets orbiting that star
Planets Orbiting the Sun	Moons of Saturn and Jupiter Note: Jupiter is only about 10% larger than Saturn so 'should' be only about 33% more massive but in fact is has about 3.3 times the mass.
Planets Orbiting A Star 129 LY from Earth
Stars Orbiting Black Hole at Center of our Galaxy
Sagittarius A* is the black hole at the center of our galaxy. This video condenses 20 years of images showing stars orbiting close to that black hole. Yields a mass for the black hole of about 4.1 million times the mass of our Sun.	video

 

Actual Orbits aren't perfect circles...
Outer Planets	Eccentricity
Path of Oumuamua through solar system in 2017 e=1.20 (hyperbolic path) : largest observed at the time

 

Newton's Third Law
The 3rd law says that all forces are equal and opposite interaction forces. If the Earth is exerting a force on the Moon, resulting in the (nearly) circular orbit of the Moon around the Earth then the Moon exerts an equal force back on the Earth, resulting in a circular orbit of the Earth as well.   The two objects actually end up orbiting a point between them, called the barycenter.
Objects 1 and 2 interacting gravitationally distance between them: \( d = r_1 + r_2 \) For each: \( F=G m_1 m_2 / d^2 \)  F = ma = mar = mv2/r  Same period for both: T=2πr/v or v=2πr/T  Leads to: \( m_1 r_1 = m_2 r_2 \) Combine with \( r_1 + r_2 = d \) and:   \( r_1 = (\frac{ m_2 }{ m_1 + m_2 }) d \) Earth-Moon : \( m_1 = 81 m_2 \hspace{1em} d=384400~km\)   \( r_1 = (384400~km)/82 = 4688~km \)  compare to radius of the earth: 6370 km Sun-Jupiter : \( m_1 = 1048 m_2 \hspace{1em} d=778,500,000~km \)   \( r_1 = (778,500,000~km)/1049 = 742,000~km \)  compare to radius of the Sun: 700,000 km	Impact of Jupiter on the Sun (Many of the first exoplanets were discovered this way.)