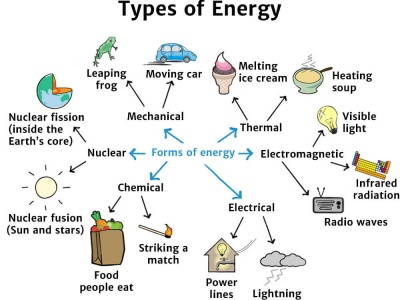
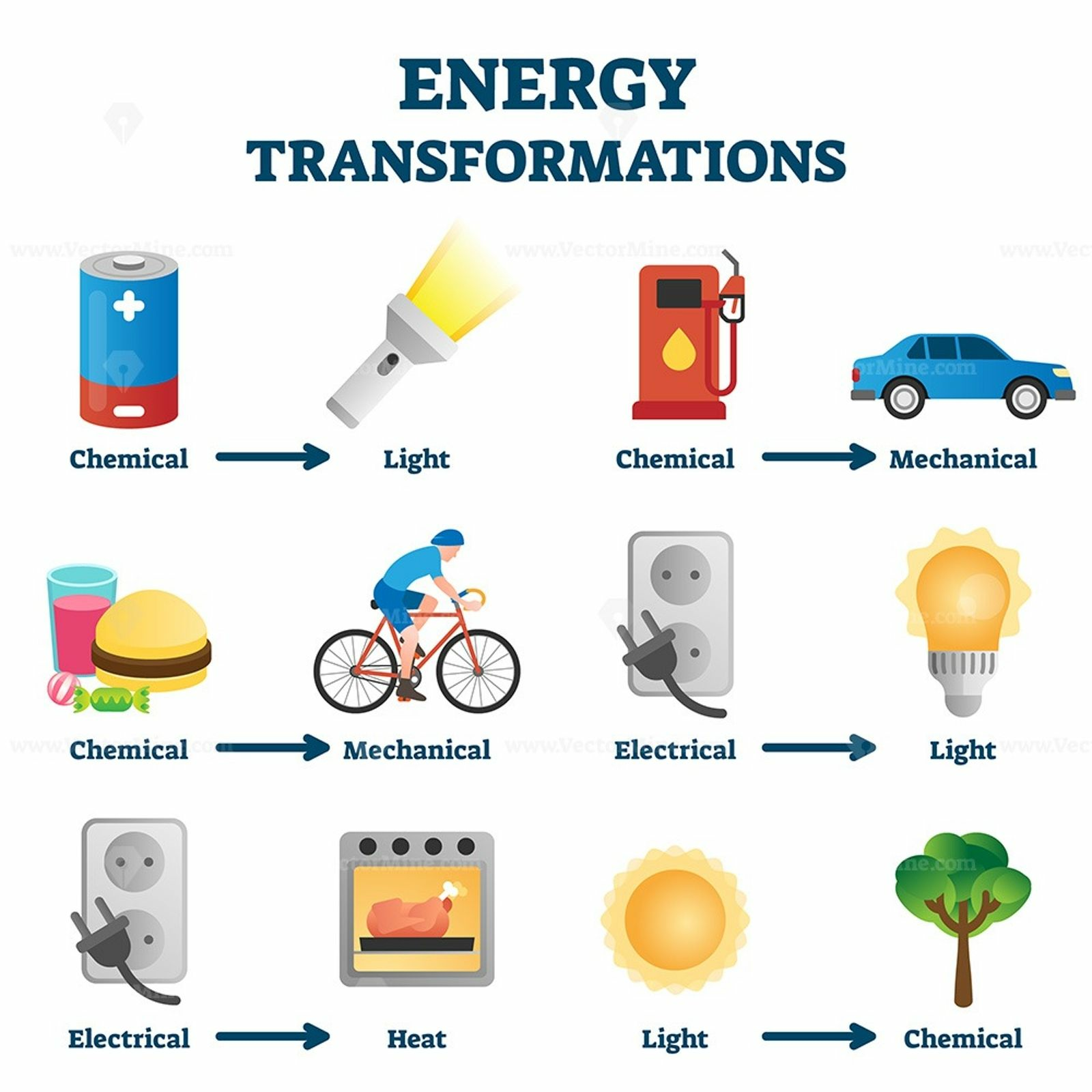
Forms of Energy
| Chapter 07 : Work and Energy |
|
Overview | |
|
Chapters 1 through 6 MICRO-management of an object's motion
|
Chapters 7 through 9 MACRO-management of an object's motion
|
|
Forms of Energy | |
|
|
|
|
Kinetic Energy | |
|
Object of some mass m travelling at some speed v Kinetic energy: K = ½ mv2
UNITS
|
Examples
|
Other Forms of Energy | ||
| Type | Example | Amount |
|---|---|---|
chemical | 1 Snicker's candy bar | 271 C = 271000 c = 1,130,000 J |
chemical | 6 inch Subway club sandwich | 1,600,000 J = 1.6 MJ |
chemical | gasoline | 47.2 MJ/kg (132 MJ/gallon) |
electrical | supercapacitor | 1 MJ/kg |
electro-chemical | Lithium-ion battery | 1 MJ/kg (phone: ~8000 J) |
electro-chemical | lead-acid car battery | 0.1 MJ/kg ( ~3 MJ ) |
nuclear | U-235 | 79,500,000 MJ/kg |
E=mc2 | anti-matter | 90,000,000,000 MJ/kg |
|
The concept of WORK done by a force | |
|
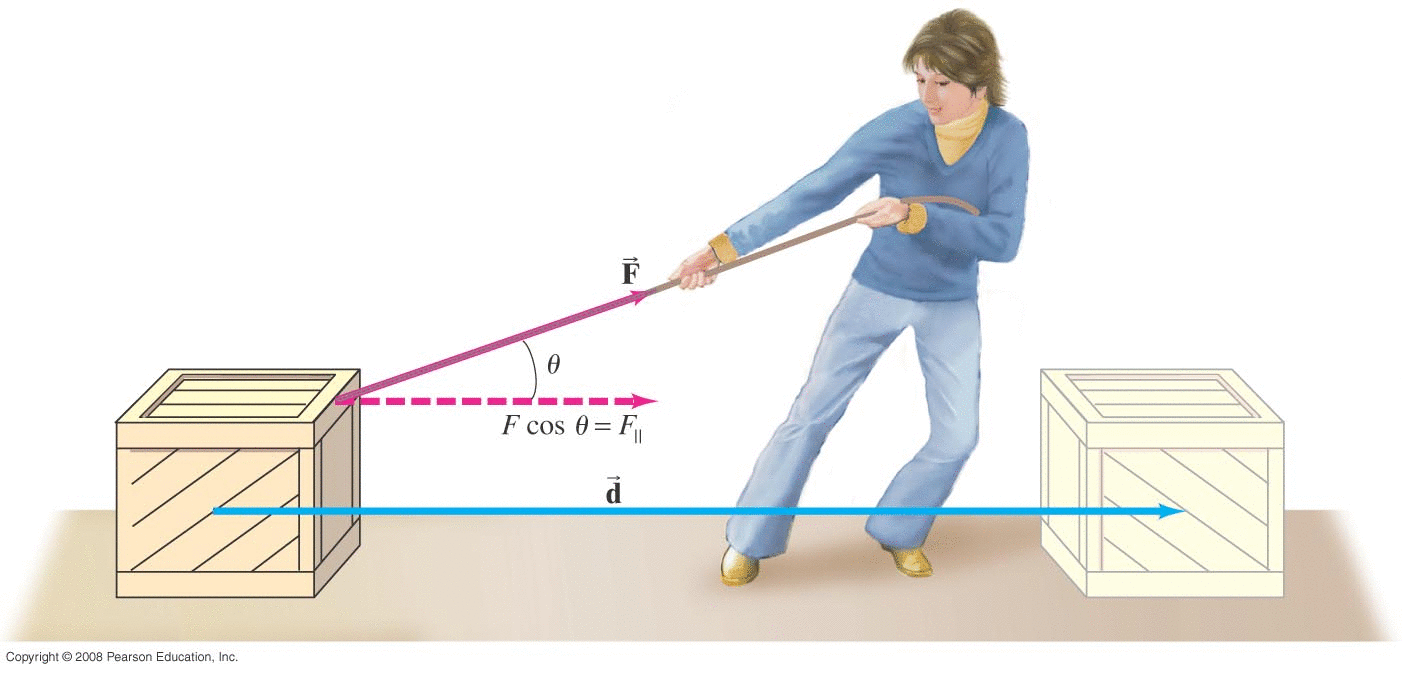
A 50 kg crate is being pulled with a force of F=100 N at a 37o angle as shown. If it is initially moving to the right at 1 m/s, how fast will it be moving after displacing 2 m to the right? (Assume no friction here.)
|
 |
|
Let's do this completely symbolically and morph the solution into one that focuses on the energy of the crate. Newton's Laws plus equations of motion result in: \( \frac{1}{2}mv^2 = \frac{1}{2}mv^2_o + F_{pull} d \cos{\theta} \) That final term must be the energy that the pulling force added to the object. The energy added (or removed) by a force acting on an object is called the WORK done by that force on the object. |
|
|
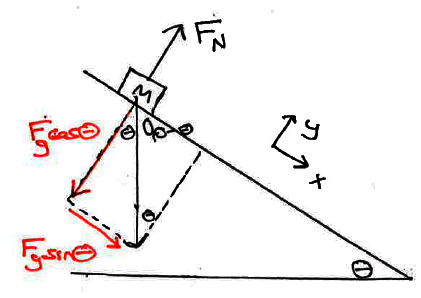
Another Case : Object Sliding Down Frictionless Incline | |
|
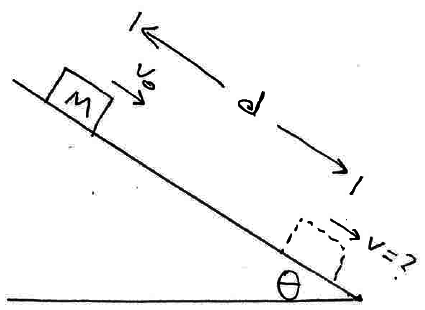
Object initially sliding down ramp at speed vo. How fast will it be moving after travelling a distance d?
|
|
 |
 |
|
Apply Newton's Laws and rearrange into an energy version: Result: \[ K_f = K_o + F_g d \cos{\phi} \] NOTE that \( \phi \) here is the angle between the direction of the force vector and the direction of the displacement vector, so you may have a 'propagate angles' around the figure. |
|
|
Work and the 'Dot' Product | |
|
The energy added (or removed) by a force acting on an object is called the WORK done by that force on the object. Mathematically: we're taking two vectors \( \vec{F} \) and \( \vec{d} \) and creating a scalar using a special type of vector multiplication called the dot product (also known as the scalar product) of the two vectors: \[ \vec{F} \cdot \vec{d} = |\vec{F}|~|\vec{d}|~\cos{\phi} = Fd\cos{\phi} \] where: F is the magnitude of the force \( F = |\vec{F}| \) so is always positive (or zero) d is the magnitude of the displacement \( d = |\vec{d}| \) so is always positive (or zero) \( \phi \) is the (interior) angle between the force and displacement vectors
|
|
|
Scalar (dot) product of two vectors \[ \vec{A} \cdot \vec{B} = AB\cos{\theta} \] where A, and B are just the magnitudes of the two vectors, and θ is the (interior) angle between them. NOTE: since the symbol θ is often used to represent the slope of a ramp or some other angle in the figure for a problem and there are usually multiple forces acting, I usually use a different symbol for the dot product: \( \boldsymbol{\phi} \) (the lowercase Greek letter phi) |
|
|
Example | |
|
Suppose we have an object moving up an incline, displacing \[ \vec{d} = (3\hat{i} + 2\hat{j})~m \] (using the coordinate system shown in the figure) Multiple forces may be acting on this object, but we want to determine the work that one particular force did: \[ \vec{F} = (-4\hat{i} + 3\hat{j})~N \]
|
 |
|
Work-Kinetic Energy Theorem | |
|
The idea here is that each force (individually) is adding or removing energy from the object so:
For each force acting on the object, compute the work done by that force on the object: \[ W_i = \vec{F}_i \cdot \vec{d} = Fd\cos{\phi_i} \] Adding all those energies to the initial K of the object yields the final K \[ K_{final} = K_{initial} + \sum W_i \] In words: for each force F acting on the object, we compute the work done by that force (i.e. the energy added or removed from the object) by taking the dot product of that force and the displacement (vector) of the object. Adding all those 'works' to the initial kinetic energy yields the 'final' kinetic energy of the object. Notes:
| |
|
Example | |
|
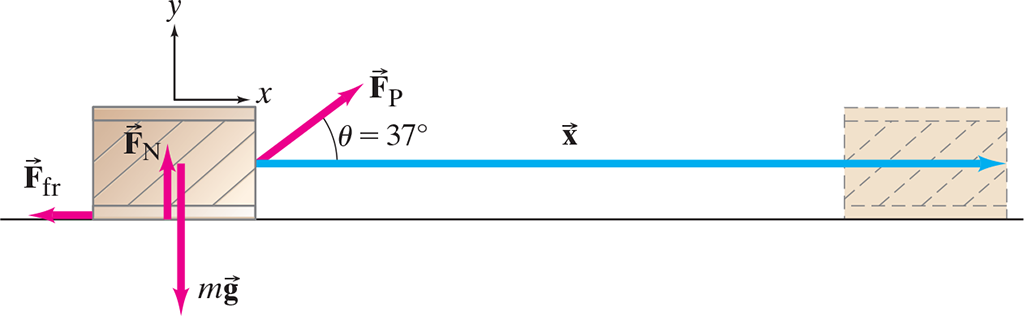
A 50 kg crate is being pulled with a force of F=100 N at a 37o angle as shown. If it is initially moving to the right at 1 m/s, how fast will it be moving after displacing 2 meters to the right? Assume the coefficient of kinetic friction between the crate and the floor is μk = 0.2 | |
|
\( K_o = ~ ? \) \( W_{F_{p}} = \vec{F}_p \cdot \vec{d} = ~ ? \) \( W_{F_{N}} = \vec{F}_N \cdot \vec{d} = ~ ? \) \( W_{F_{g}} = \vec{F}_g \cdot \vec{d} = ~ ? \) \( W_{F_{fr}} = \vec{F}_{fr} \cdot \vec{d} = ~ ? \) \( K_f = ~ ? \) \( v_f = ~ ? \) |
 |