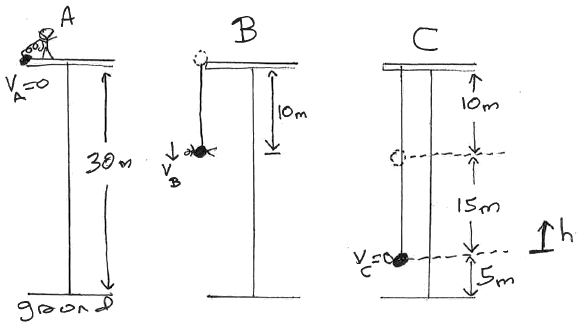
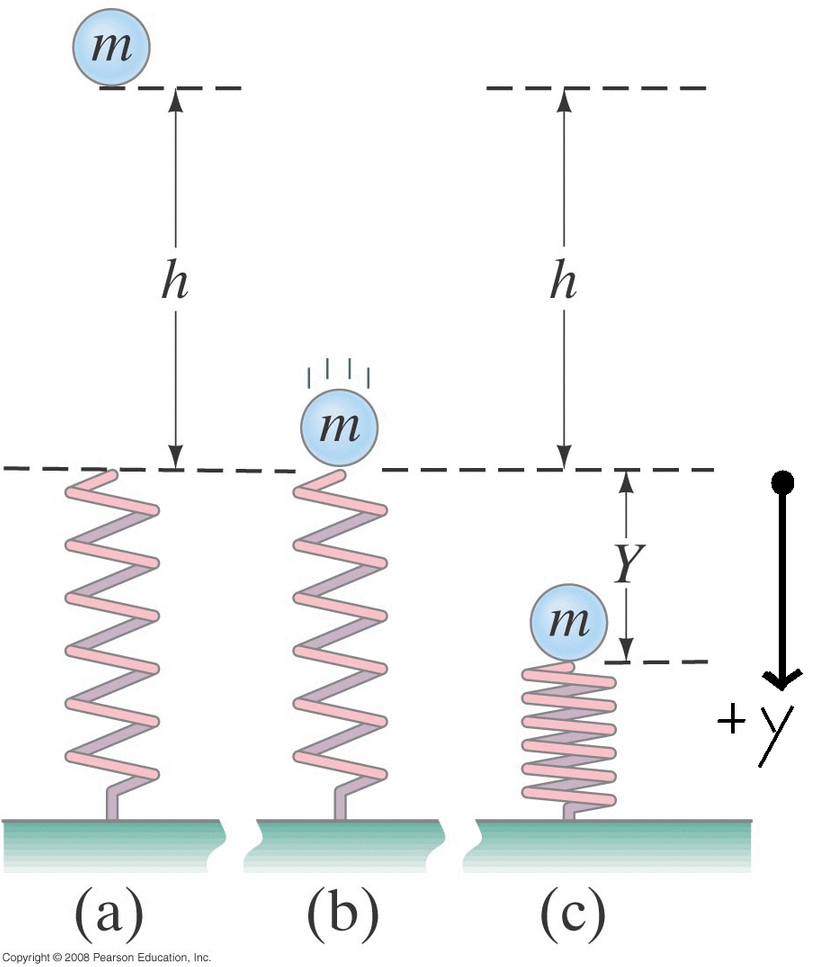
Work Done by Varying (non-constant) Forces
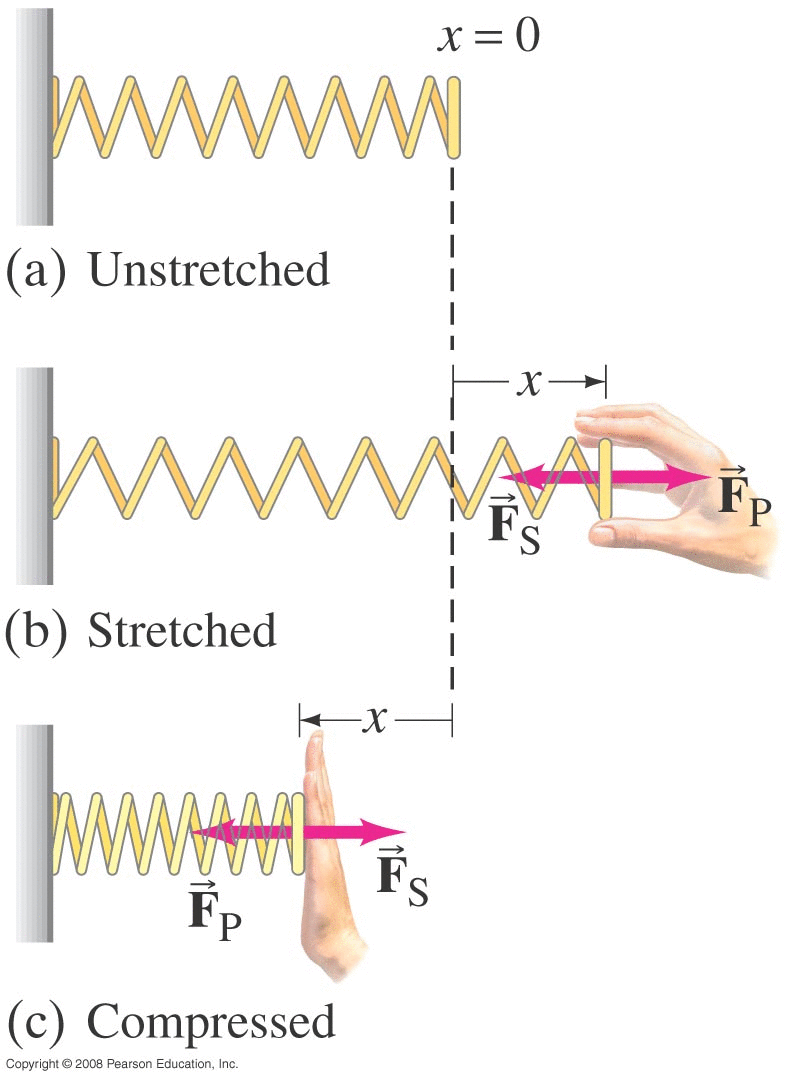
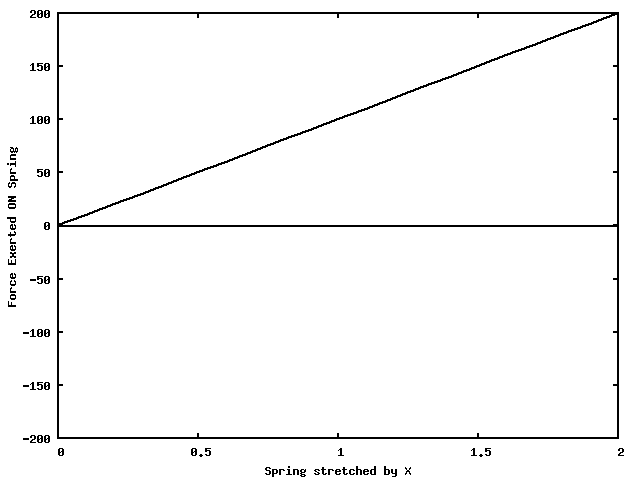
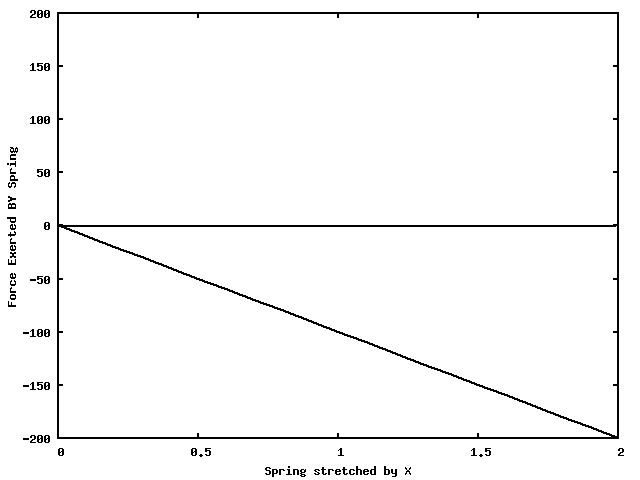
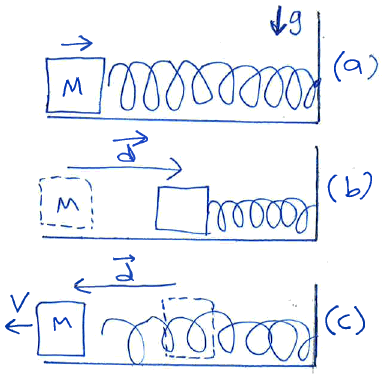
Suppose an object travels along a path from (a) to (b). Multiple forces may be present, and some may not be constant (like the \( \vec{F} \) shown here). On each little dl step, a tiny amount of work in done: ΔW: \[ \Delta W_i = \vec{F}_i \cdot \Delta \vec{l}_i = F_i \Delta l_i \cos{\theta{i}} \] Adding up all the steps: \[ W = \sum \Delta W_i = \sum \vec{F}_i \cdot \Delta \vec{l}_i = \sum F_i \Delta l_i \cos{\theta{i}} \]
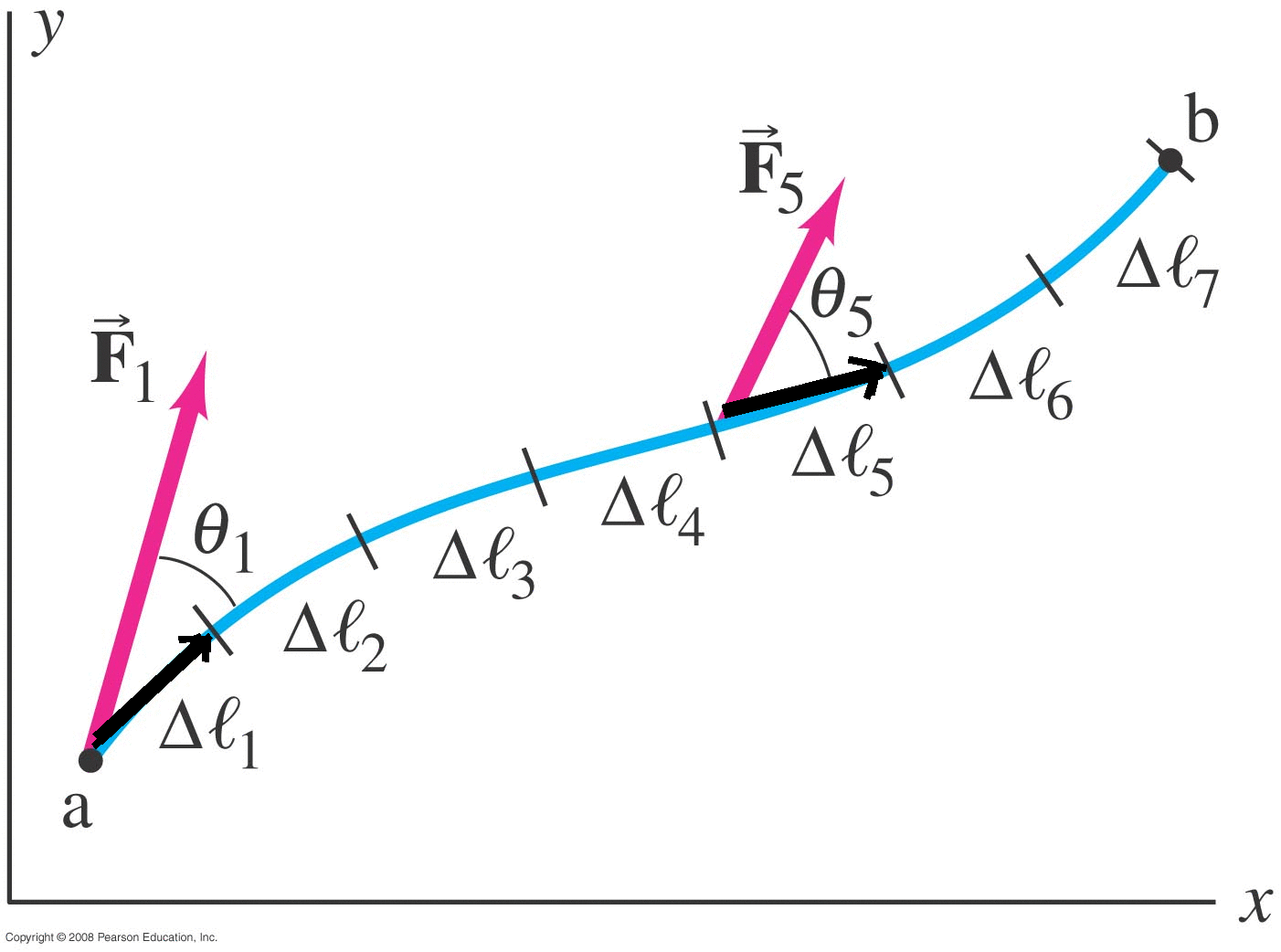
As we shrink the Δl steps down to infintesimal dl calculus steps, this becomes: \[ W = \int_a^b \vec{F} \cdot d\vec{l} \]   If the force is constant, it comes out of the integral, leaving just: \[ W = \vec{F} \cdot \int_a^b d\vec{l} \] but that integral is just \( \vec{d} \) so we just have: \[ W = \vec{F} \cdot \vec{d} \] as we've been using so far.

 

Linear Restoring Forces
The general result above gives us a way to deal with non-constant forces, but only if we can 'do the integral'. One (very) common force falls into that category: the linear restoring force. In this case we can 'do the integral' without actually doing it! (We just have to remember how to do the area of a right triangle...)
PROPERTIES OF LINEAR RESTORING FORCES Force (linearly) proportional to displacement from equilibrium In opposite direction to displacement First order approximation:         Fs = -kx These are also called elastic forces, so sometimes seen as:         Fel = -kx EXAMPLES springs pendulum (almost) pressure waves (sound) structure response to wind stringed musical instruments

Force Exerted ON spring

Force Exerted BY spring

 

Example: Object Sliding into Spring

Note: we'll use this problem to illustrate how to determine the work done by linear restoring forces. (I.e. how to 'do the integral' without actually using calculus.)   A 10 kg box slides along a horizontal frictionless surface to the right at vo = 2 m/s. It encounters a spring with k = 200 N/m that has one end attached to a wall. How far will the spring compress before bringing the box to a stop? (Use Work-K) What are the forces on the box at that point? How fast will the box be moving when it bounces off the spring? (Use Work-K)   WHAT IF there is friction on the floor (but just underneath where the spring is located), with μk=0.1? How far will the spring compress now?

 

Example: Bungee Jump
A 100 kg person steps off the top of a ledge. Their bungee cord has a length of 10 m and they want to stop 5 meters before hitting the ground below, so at this location they need to come to a stop after the cord has stretched by 15 m. What spring constant does the bungee cord need to have? What happens if someone with a different weight uses the same cord?	Be careful here: a bungee cord is NOT entirely equivalent to a spring; it's more like a 1-way spring. It exerts a force when stretched but not when compressed.

 

Example: Object Dropped onto Spring

A 2 kg object is dropped (from rest) onto a spring 50 cm below.   How much will the spring compress if the spring has a force constant of k=2000 N/m?     I'll use the same notation as the book did for this problem and call Y the positive amount that the spring has been compressed. (I normally use 'd' to represent that.) For example Y=10 cm would mean that the object ends up 10 cm BELOW where the top of the spring used to be. It also means (when we're setting up the equation here) that the displacement from (a) to (c) will be d=h+Y (with h=50 cm and Y the thing we're looking for). We're going to end up with a quadratic equation here, and knowing we're looking for the Y solution that's positive will let us choose which solution is 'right'.

 

Linear Restoring Forces and Differential Equations
Most of you will take a DFQ class - why? Apply Newton's Laws:   Linear restoring force (F=-kx) so this becomes:     Rearranging:	\[ \sum F_x = m a_x \]   \[ -kx = m a_x = \frac{d^2 x}{dt^2} \]   \[ \frac{d^2 x}{dt^2} = -\frac{k}{m}x \]
The object's motion then will be whatever x(t) function solves that equation.
Note that differentiating this function twice returns you back to the original function (with a minus sign in front, and a constant coming out in the process). What are the ONLY functions x(t) that have this property? sin(ωt) cos(ωt) (and any linear combination of those two) with \( \omega = \sqrt{k/m} \) Linear Restoring Functions lead to periodic (sinusoidal) behavior.