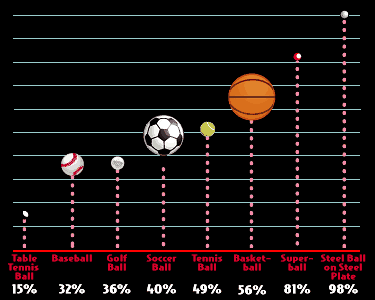
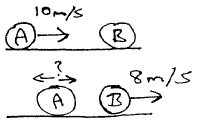
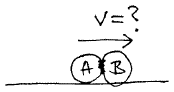
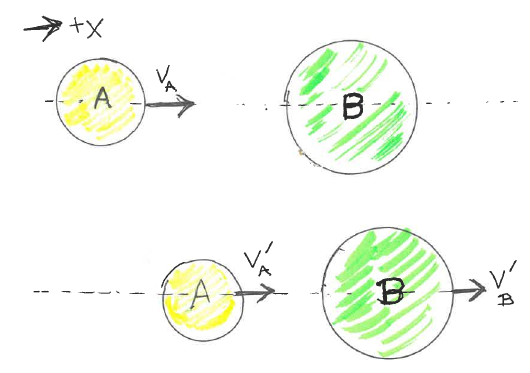
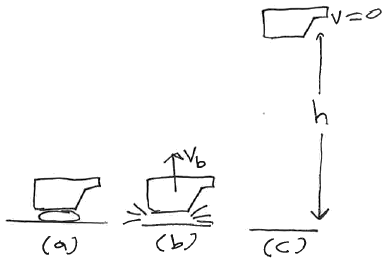
A Couple of Bat/Ball Collision videos
video 1 (at 20 sec)	video 2 (at 2:00)
Real Version of Newton's Laws
Implications
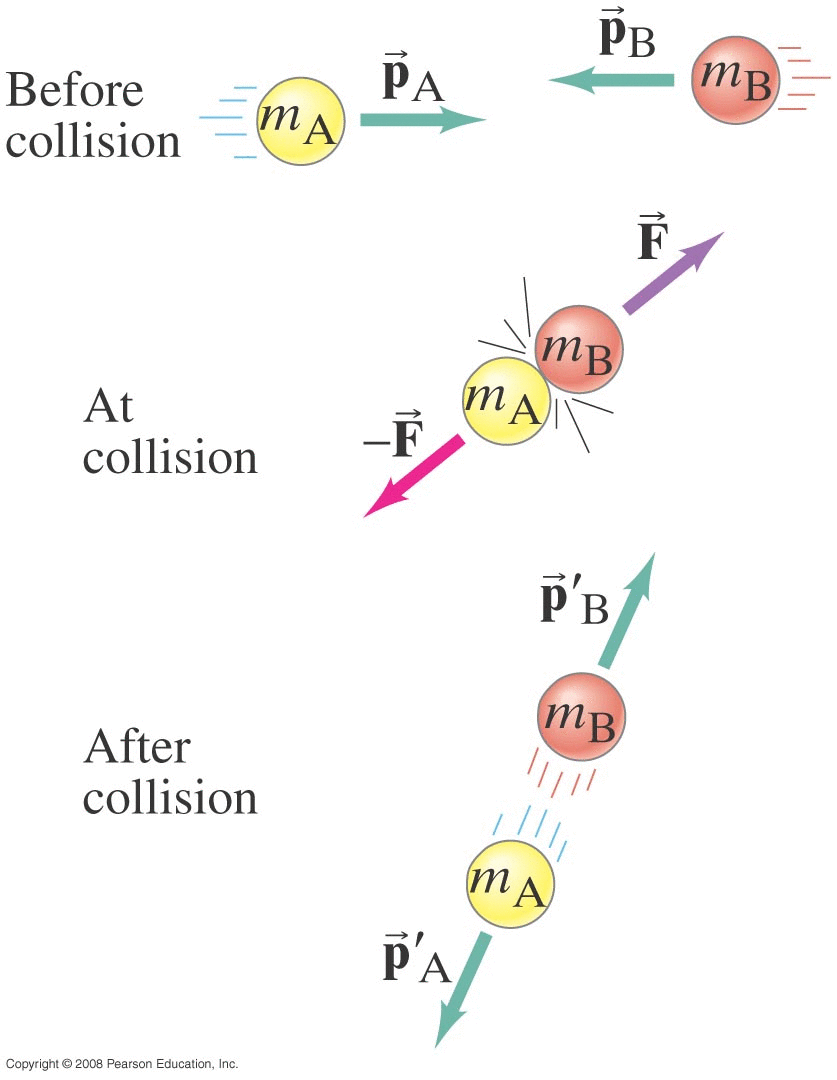
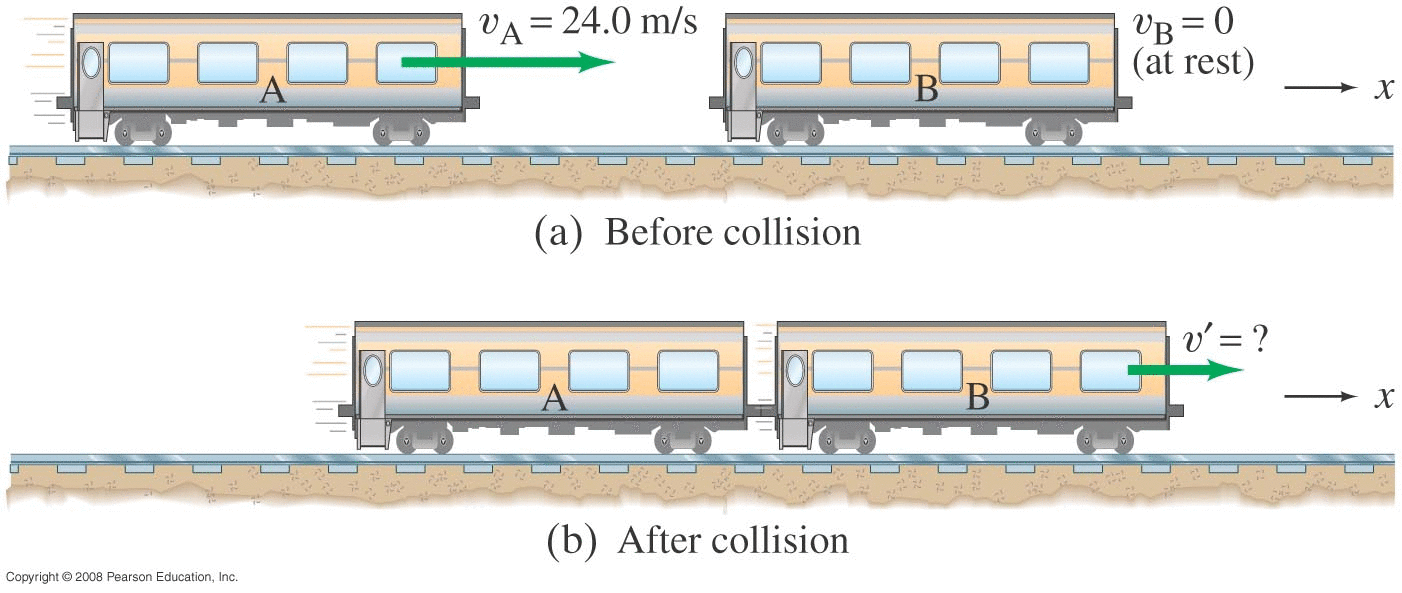
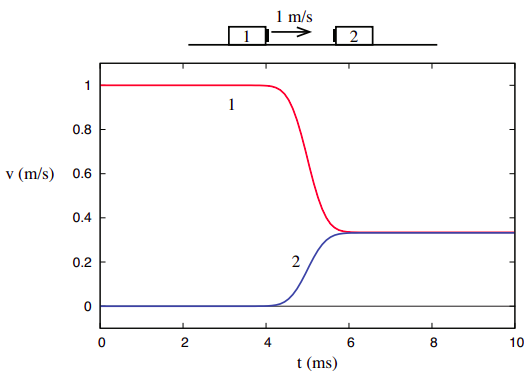
If we see an object change its momentum over some interval Δ t, we can determine the average force that must have been acting on it (Ball hit by bat, car collision, explosion, ...)	\[ \vec{F}_{avg} = \frac{ \Delta \vec{p} }{ \Delta t } \]
Rearranging:	\[ \Delta \vec{p} = \int \vec{F}(t) dt \]
If constant mass, then:	\[ \vec{v}(t) = \vec{v}_o + \frac{1}{m} \int \vec{F}(t) dt \] giving us a way to handle time-varying forces

 

Conservation of Momentum
Consider two objects interacting via some force.     (Could be anything: electrical, gravitational, contact ('normal') force, etc)
Force that A exerts on B causes B's acceleration: \[ \vec{F}_{A~on~B} = m_B\vec{a}_B = m_B \frac{ d\vec{v}_B }{dt} \] Force that B exerts on A causes A's acceleration: \[ \vec{F}_{B~on~A} = m_A\vec{a}_A = m_A \frac{ d\vec{v}_A }{dt} \] Newton's Third Law: \[ \vec{F}_{B~on~A} = -\vec{F}_{A~on~B} \] Implies: \[ m_A \frac{ d\vec{v}_A }{dt} = -m_B \frac{ d\vec{v}_B }{dt} \] Rearrange: \[ m_A \frac{ d\vec{v}_A }{dt} + m_B \frac{ d\vec{v}_B }{dt}=0 \]
In terms of momentum: \[ \frac{d\vec{p}_A}{dt} + \frac{ d\vec{p}_B}{dt} = 0 \] or: \[ \frac{d}{dt} ( \vec{p}_A + \vec{p}_B ) = 0 \] so: \[ \vec{p}_A + \vec{p}_B = constant = \vec{p}^\prime_A + \vec{p}^\prime_B \]
Same idea holds for multiple interacting objects. When objects interact, the total momentum of the system remains constant. We say that: Momentum is CONSERVED. In mathematical language: \[ \sum \vec{p}_{before} = \sum \vec{p}_{during} = \sum \vec{p}_{after} \]

 

Example: Train Car Collision
Let's start with a simple 1-D collision, where one of the objects in initially at rest: A 10,000 kg railroad car (A) moving down the track at 24 m/s collides with a 15,000 kg car (B) that was initially at rest. Suppose that when they collide, the cars lock onto each other.
What is their common speed after the collision? Look at the mechanical energy before and after the collision. Is it conserved? A high-speed video of the collision shows that the interaction took 20 ms.   (a) What force did A exert on B?   B on A?   (b) What acceleration did each undergo during the collision?

 

Collisions are not Instantaneous

What does that wording above mean about the interaction taking 20 ms?

 

Example: Bouncing Balls
A 0.1 kg ball is dropped from a height of 1 meter. It lands on a hard, horizontal floor and bounces back up to a height of 80 cm. How much force did the floor exert on the ball if the two were in contact for Δ t = 10 ms? How much energy was lost in the collision? What does CoM imply here? What is the 'other object' the ball is colliding with?

 

Collision : Bullet and Block of Wood
A 5 g bullet travelling horizontally at 300 m/s strikes a 2 kg block of wood sitting on a frictionless surface, initially at rest. The bullet embeds itself in the wood.
How fast will the (combined) object be moving right after the collision? How much energy was lost in the collision? If the collision took Δ t = 0.1 ms what force was involved? Compare that force to the other forces present in the problem like gravity, normal force, friction, ...
Major Warning
When collisions (or explosions) are involved: Mechanical Energy is normally NOT conserved (there is 'other work' present) The force of the collision overwhelms nearly any other force present If a collision (or explosion) occurs somewhere in a scenario, isolate the that event. CoE can be used up to that point, and again after that point, but during the collision/explosion, we can ONLY count of CoM being true still.

 

Explosion : Grappling Hook Launcher
In an old Mythbusters episode, they test-fired a grappling-hook launcher. The 'launcher' (essentially a little cannon) was placed on a table and an explosive charge inside the barrel was set off, sending the grappling hook horizontally (to the right) at a speed of 40 m/s. As a result, the launcher itself recoiled backwards (to the left), where a shock absorber (a spring) kept it from hitting the wall. (Note: ignore friction here.)	Mass of grappling hook: 10 kg. Mass of (unloaded) launcher: 80 kg. Spring constant: k=50,000 N/m.
Determine: How far did the launcher push the spring in? How much energy was ADDED to the system by the explosion? If the explosion took 2 ms: How much force did the launcher 'feel'? How much force did the hook 'feel'?

 

Ballistic Pendulum
Suppose we hang a 1 kg block of wood from a ceiling on a 1 m long string. A 5 g (0.005 kg) bullet comes in from the left at 300 m/s and embeds itself into the block. How far out does the block swing as a result?

 

Characterizing Collisions
INELASTIC Collision Some Mechanical Energy lost : this is nearly all collisions. Example: Two identical balls of mass M=0.17 kg Ball A at 10 m/s strikes ball B initially at rest. After collision, we see B moving off at 8 m/s. Find vA after the collision and the total energy before and after
TOTALLY INELASTIC Collision Objects 'stick together' in the collision Maximum loss of Mechnical Energy Example: Two identical balls of mass M=0.17 kg Ball A at 10 m/s strikes ball B initially at rest. Objects stick together Find v after collision Find energy loss
ELASTIC Collision (RARE) Mechanical Energy IS conserved Example: Two identical balls of mass M=0.17 kg Ball A at 10 m/s strikes ball B initially at rest. After collision, we note that A came to an immediate stop. Find vB after the collision and the total energy before and after

 

Elastic Collision
(Basically HW09-28 but with integer values everywhere to make the math simpler!)   A 2 kg hockey puck, moving in the +X direction with a speed of 8 m/s has a head-on collision with a 4 kg puck, initially at rest. Assuming an elastic collision, what will be the velocities of each object just after the collision? Tookit : CoM (1d here); CoE (basically just K)

 

Super-specialized equations

Super-specialized equations (dangerous!), ONLY VALID WHEN: 1-D collision Must be ELASTIC (energy conserved) (Common at the scale of atoms; non-existent up at our scale...) Object B initially at rest Object A hits it at vA (These conditions will NOT be present in any test problems...) Velocities after collision: \[ v^{\prime}_A = v_A ( \frac{m_A - m_B}{m_A + m_B} ) \] \[ v^{\prime}_B = v_A ( \frac{ 2 m_A }{m_A + m_B} ) \] If mA = mB : A stops, B moves off at the same velocity A had If mA < mB : A bounces backwards, B moves off in A's original direction If mA > mB : both objects move in A's original direction

 

Additional Example : Explosion : Anvil Toss
In the anvil-toss example we did back in the 1-D and 2-D motion chapters, a 90 kg anvil was launched via an explosive and ended up reading an apogee height of 78.4 m. (Assume it went vertically straight up for this example.) How much energy was released in the explosion? If the detonation took Δ t = 0.1 ms what force did the explosion exert on the anvil?   (How is momentum being conserved here?)

 

Additional Example : Pendulum with Elastic Collision
Two balls of masses mA = 40 g and mB = 60 g are suspended on 30 cm long strings as shown in the figure. The lighter ball is pulled away to a 66o angle and released at rest. Assume that the balls are made of a material that allows this to be an elastic collision.
What is the velocity of the lighter ball just before impact? What is the velocity of each ball just after the elastic collision? What will be the maximum height of each ball after the elastic collision?