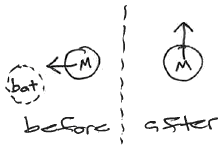Summary so far

An object's change in momentum is related to the (average) force (vector) acting on it: \[ \vec{F}_{avg} = \Delta \vec{p} / \Delta t \] Conservation of Momentum : when objects interact, the total momentum of the system remains constant. \[ \sum\limits_{before} \vec{p} = \sum\limits_{during} \vec{p} = \sum\limits_{after} \vec{p} \]   Mechanical Energy is usually NOT conserved (there's some other work present) Inelastic Collision (the normal type by far) : some mechanical energy lost Totally Inelastic Collision (objects stick together) : maximum loss of mechanical energy Elastic Collision (very rare) : mechanical energy conserved

 

Vector Collision : Baseball+Bat
A 0.145 kg baseball flying horizontally at 32 m/s strikes a bat and is popped straight up to a height of 36.5 m. The contact time between the bat and the ball is 0.7 ms (typical), calculate the average (vector) force the bat exerted on the ball during contact.   We'll talk about the concept of impulse ( \( \vec{J}=\Delta \vec{p} \) ) here also.

 

2-D Vehicle Collision

A 1000 kg car travelling east at 20 m/s collides with a 2000 kg truck travelling north at 15 m/s. Assume this is a totally inelastic collision (objects 'stick together' as a result of the collision). (Assume the given masses represent the total mass of each object: car, passengers, etc.) At what angle does the combined object move off? If each driver has a mass of 100 kg, determine the force on each driver if the collision took Δt=0.1 s

 

2-D Asteroid Collision

A 100 kg spacecraft travelling in the +X direction at 200 m/s collides with a 5000 kg asteroid. (We're using a coordinate system attached to the asteroid at this instant, so it's velocity would be zero.) After the collision, the spacecraft dislodges a 1000 kg chunk of the asteroid and they move off together as shown.

What must the velocity of the remaining 4000 kg part of the asteroid be? How much energy was lost in the collision? (See the Sept 2022 NASA 'DART' mission where a probe was deliberately crashed into an asteroid as a test of an Earth-bound asteroid defense system.)

 

Example: Poolballs (old test problem)
Two pool balls are touching one another on a flat, frictionless, horizontal pool table as shown in the figure. We shoot the cue ball (labeled with a 1) towards them with a speed of 6 m/s at the 45o degree angle shown. The balls all have identical masses of 0.15 kg.	Coordinates: +X to the right, +Y towards the top of the page
Right after the balls collide, we observe that: ball 2 heads straight in the +X direction with a speed of 2 m/s ball 3 heads off at the 30o angle shown with a speed of 3 m/s. (No information is given here about the radius or mass distribution, so just treat these as point masses.) What is the vector velocity of the cueball right after the collision? \( \rule{0.8in}{0.01in}\hat{i}+\rule{0.8in}{0.01in}\hat{j})~~(m/s) \) How much energy was lost in the collision? \( \rule{0.8in}{0.01in}~J \)

 

Additional Example : Objects Held Together with a Spring

Two boxes (on a frictionless surface) are pushed together with a spring between them and held in place (at rest). The spring has k=48000 N/m and in figure (a) it's compressed by 5 cm. When they're released, how fast will each box be moving when they separate from the spring? (Unlike an explosion, all the energy initially stored in the spring will be transferred to the objects, so we can use CoM and CoE together here.)

 

Additional Example : Objects Colliding with a Spring

Two boxes are sliding towards each other on a frictionless, horizontal surface as shown in the figure. A spring with k=48000 N/m is placed between them. The spring causes each object to slow down, reaching a point where they're moving together at the same velocity (which will also be the point of maximum compression for the spring). How fast are they moving together at this point? How much did the spring compress? The compressed spring will eventually push the boxes apart. How fast will each be moving when they separate?   (This is an elastic collision: there's no mechanism for energy loss here - the two objects never actually touch one another.)