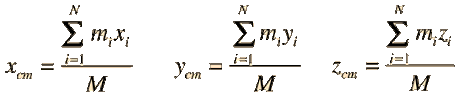|
Why is the CM concept relevant/important?
|
|
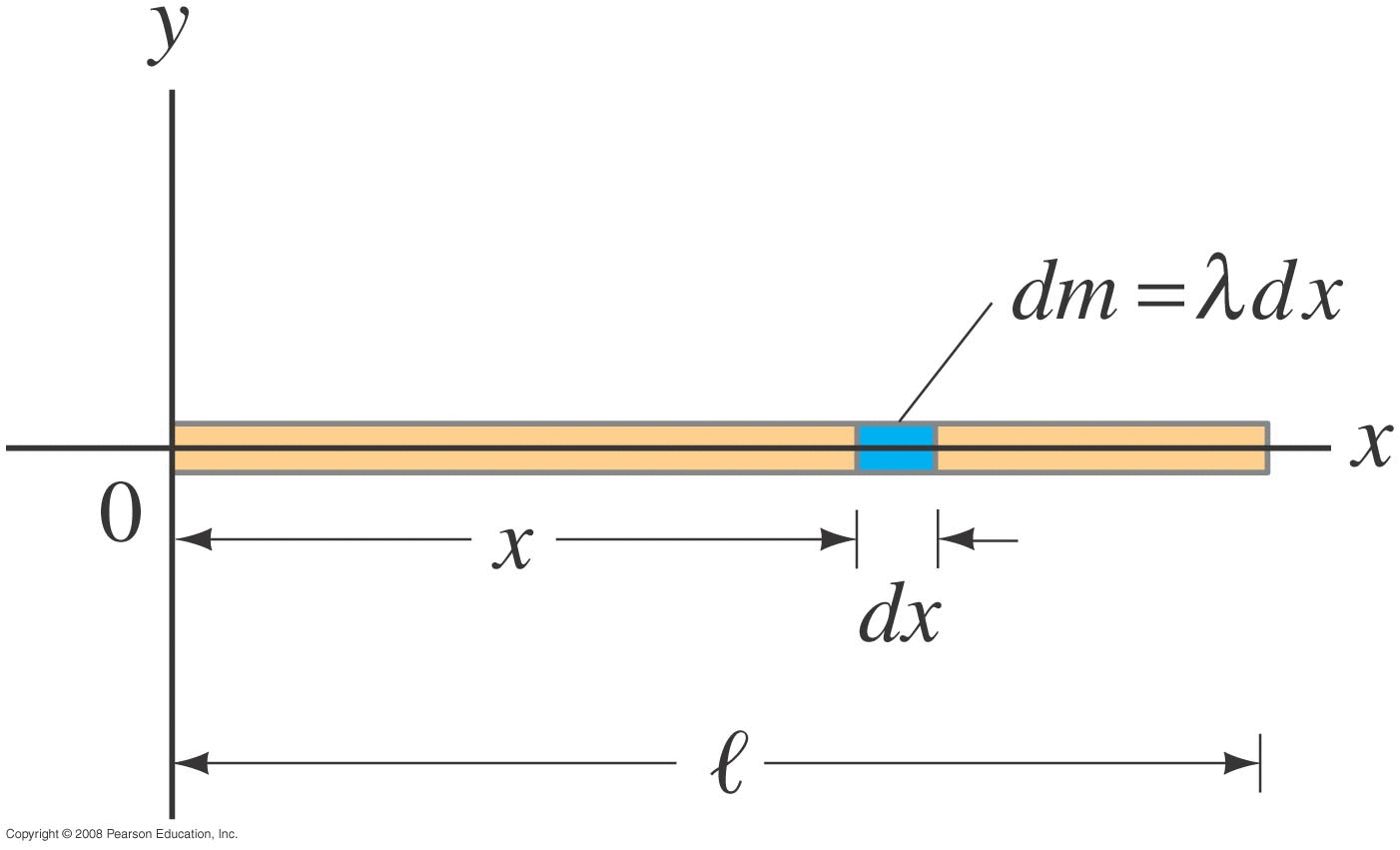
Suppose our object is a collection of point-masses (could be ball bearings
connected by springs, or maybe a calculator and it's gazillions of 'point-mass'
molecules.
|
Start with definition: |
\[ \vec{r}_{cm} = \frac{1}{M} \sum m_i \vec{r}_i \] |
Rearrange into: |
\[ M \vec{r}_{cm} = \sum m_i \vec{r}_i \] |
Differentiate with respect to time: |
\[ M \vec{v}_{cm} = \sum m_i \vec{v}_i \] |
Differentiate again with respect to time: |
\[ M \vec{a}_{cm} = \sum m_i \vec{a}_i \] |
Expanding out the sum a bit: |
\[ M \vec{a}_{cm} = m_1 \vec{a}_1 + m_2 \vec{a}_2 + \cdots \] |
|
Look at each term in the sum on the right. The first term is actually:
\[ m_1 \vec{a}_1 = \sum \vec{F}_1 \]
That is: it's the sum of all the forces acting on that entity (molecule?)
The right-hand side of that hugely long sum is really:
|
|
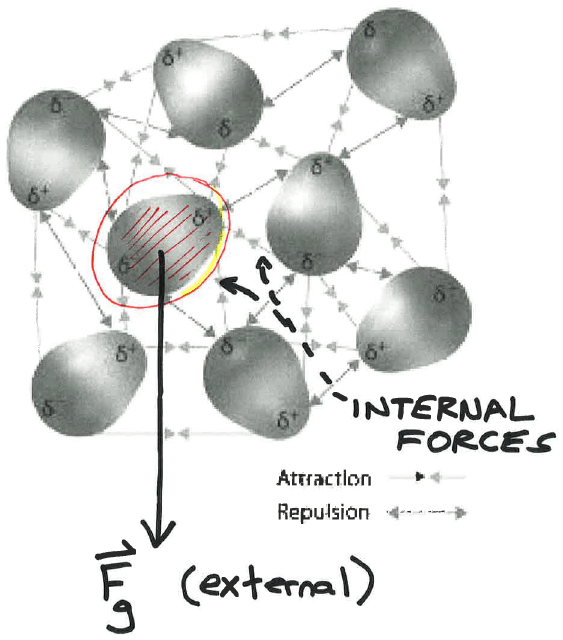
BUT : Most of those forces are INTERNAL forces (between the point-masses
or molecules making up the object)
and those all cancel each other out in pairs thanks to Newton's third law
(two objects exert "equal and opposite forces" on each other).
|
|
We're left with just: |
\[ M \vec{a}_{cm} = \sum_{external} \vec{F} \]
|
|
THIS IS A BIG DEAL
|
|
In words :
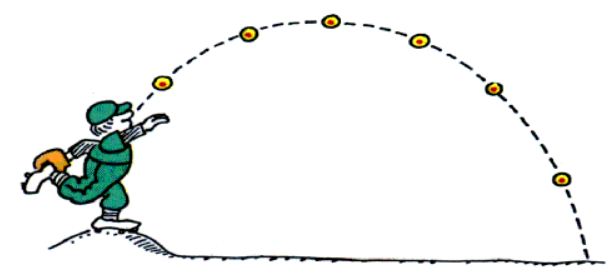
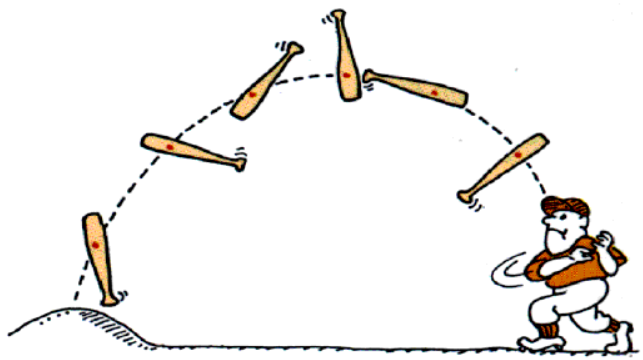
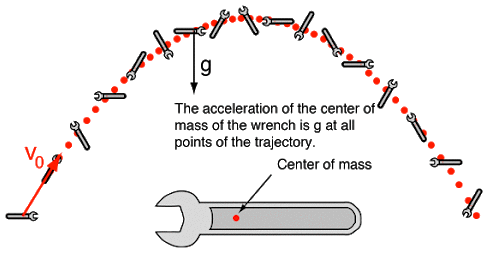
If a composite object (book made of gazillions of atoms for example)
is tossed into the air,
it's CM will follow the same path a point object
of the same mass would have.
Our point-mass model is actually fine for some types of motions of real, extended objects.
\( \sum \vec{F} = m\vec{a} \) shows us how the CM of the object will move.
The object (book, etc) can (and almost certainly will) ROTATE about that
center of mass point though, and that's what the remainder of the course will focus on:
angular motion, and the forces (torques)
that cause that rotational motion.

|
|
Example : Composite Object
|
|
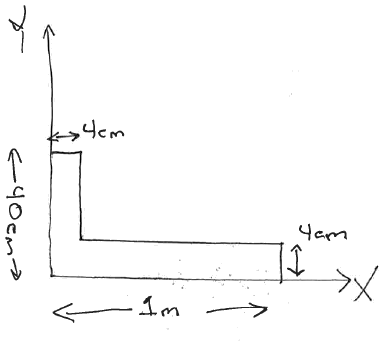
Determine the CM of the thin L-shaped object
shown (carpenter's square).
Assume the density/area σ is constant throughout the material.
The 'trick' is to break an object into 'parts' for which
we can determine the CM easily (hopefully via symmetry arguments).
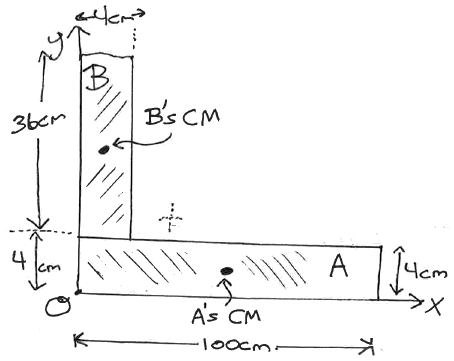
This object can be broken into two rectangular parts:
where symmetry can be used to find the CM of each part.
|
 |
|
How does that work? Start with the definition:
\[
x_{cm} = \frac{ \sum ( m_i x_i ) }{M} \hspace{2em} so \hspace{2em} \sum ( m_i x_i ) = M x_{cm}
\]
\[
But: \hspace{2em} \sum ( m_i x_i ) = \sum_A (m_i x_i) + \sum_B (m_i x_i)
\]
\[
So: \hspace{2em} M x_{cm} = M_A x_{cm,A} + M_B x_{cm,B}
\]
\[
Finally: \hspace{2em} x_{cm} = \frac{M_A x_{cm,A} + M_B x_{cm,B}}{M}
\]
|
|
In words:
Break the object into parts we can easily find the CM of.
Replace each part with a point located at the CM of that part
Use the point-mass equations to find the overall CM for the object.
|
 |