Angular Velocity
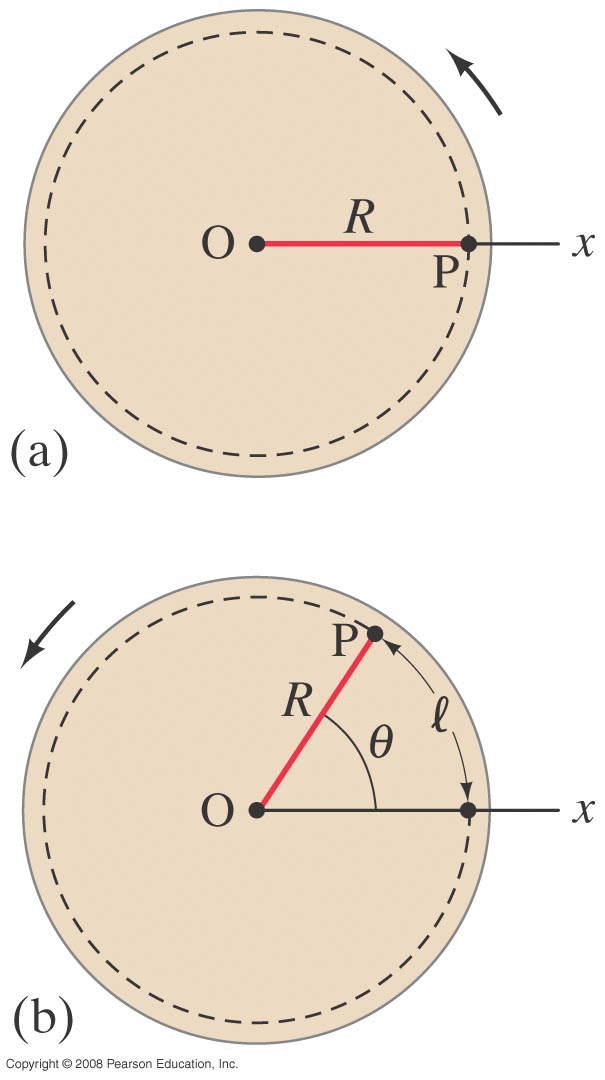
As an object rotates, every point on that object rotates through the exact same angle θ

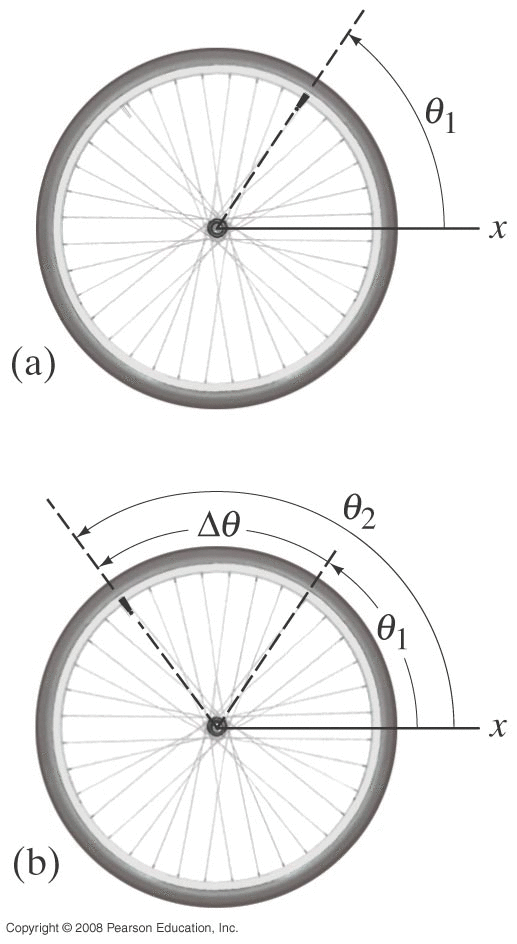
A point located a distance R from the axis of rotation will trace out a distance (arc-length) of l = Rθ Note: θ = l/R defines an angle in units of radians BUT the units on the RHS cancel, so technically it's unitless If object rotates from θ1 at t1 to θ2 at t2 : it's moved through an angle of Δθ = θ2 - θ1 in a time interval of Δt = t2 - t1 yielding an average angular velocity of ωavg = Δθ/Δt

Instantaneous Angular Velocity
Calculus limit: Δt ➔ dt   ω=dθ/dt   Symbol: lowercase omega: ω not w Units: rad/s or really just s-1

 

Vector Nature of Angular Quantities
It's called an angular velocity (as opposed to angular speed) because it actually is a vector The vector part is defined to be the direction of the axis about which the rotation is occurring via a right-hand rule.

 

Angular Acceleration

Average angular acceleration : αavg = Δω/Δt Instantaneous angular acceleration : α = dω/dt Symbol: lowercase alpha: α not a Units: (rad/s)/s   or   rad/s2   but really just   s-2

 

Angular Equations of Motion for rotation about a single fixed axis with constant angular acceleration α
Angular-motion equations	Corresponding Linear-motion equation
\[ \omega = \omega_o + \alpha t \]	\[ v = v_o + at \]
\[ \theta = \theta_o + \omega_{avg}t \]	\[ x = x_o + v_{avg}t \]
\[ \theta = \theta_o + \omega_o t + \frac{1}{2}\alpha t^2 \]	\[ x = x_o + v_o t + \frac{1}{2}at^2 \]
\[ \omega^2 = \omega^2_o + 2 \alpha \Delta \theta \]	\[ v^2 = v^2_o + 2 a \Delta x \]

 

Useful Conversions

1 cycle = 1 rev = 360o = 2π radians An object rotates through a full 360o (i.e. Δθ=2π radians) in one period (T), so: ω=2π/T    or     T=2π/ω ω=2πf      or     f=ω/(2π)