Review : Angular Equations of Motion for rotation about a single fixed axis with constant angular acceleration α
Angular-motion equations	Corresponding Linear-motion equation
\[ \omega = \omega_o + \alpha t \]	\[ v = v_o + at \]
\[ \theta = \theta_o + \omega_{avg}t \]	\[ x = x_o + v_{avg}t \]
\[ \theta = \theta_o + \omega_o t + \frac{1}{2}\alpha t^2 \]	\[ x = x_o + v_o t + \frac{1}{2}at^2 \]
\[ \omega^2 = \omega^2_o + 2 \alpha \Delta \theta \]	\[ v^2 = v^2_o + 2 a \Delta x \]

 

Useful Conversions

1 cycle = 1 rev = 1 rotation = 1 turn = ... = 360o = 2π radians An object rotates through a full 360o (i.e. Δθ=2π radians) in one period (T), so: ω=2π/T    or     T=2π/ω ω=2πf      or     f=ω/(2π) = 1/T Also commonly encountered in rotational motion: RPM : rotations per minute (very common) RPS : rotations per second (rare; usually seen as Hz - Hertz - cycles/second)

 

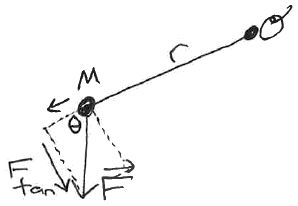
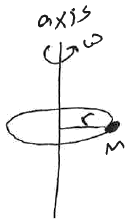
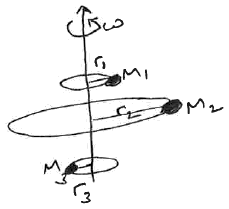
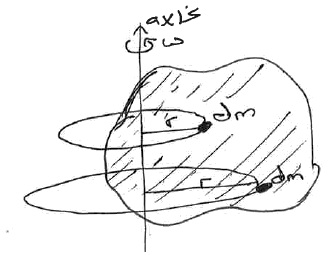
Example: Merry-go-Round (angular equations of motion)

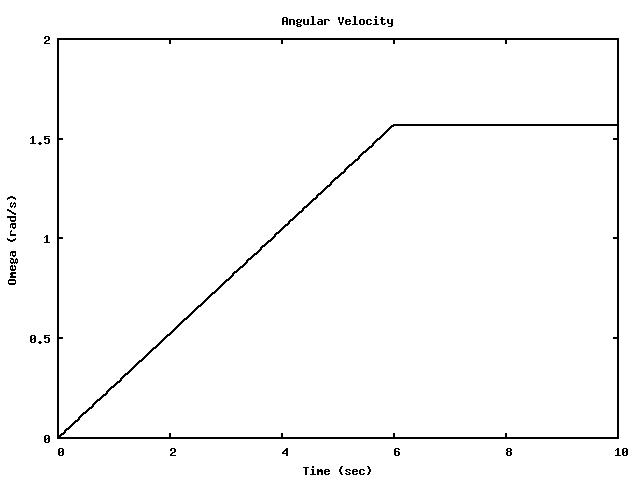
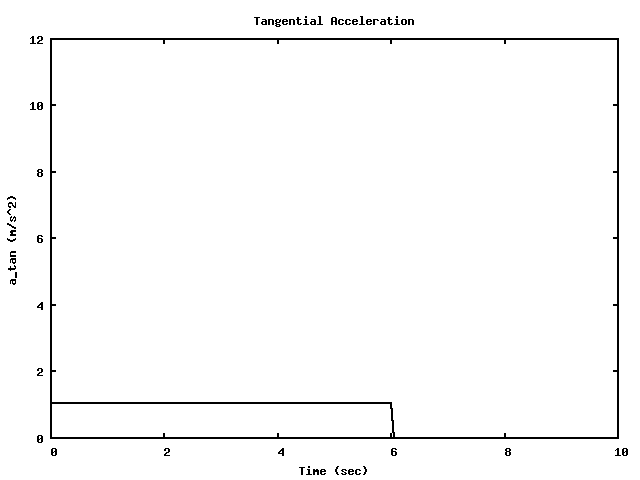
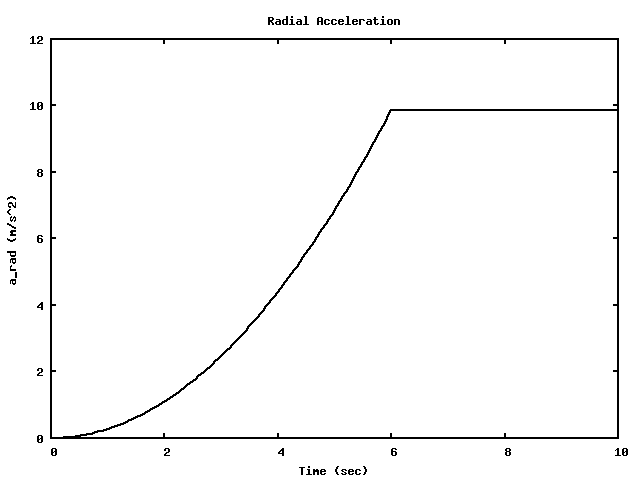
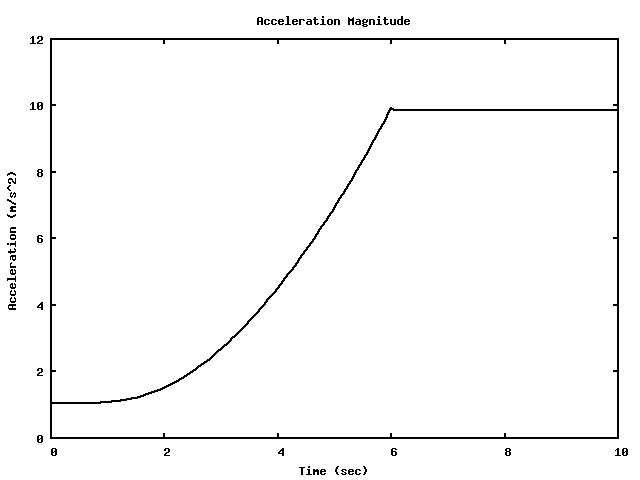
A Merry-go-Round takes 6 seconds to spin up from rest to reach it's final speed. Once it's spun up and running at a constant speed, it takes 4 seconds to make each complete rotation. What angular acceleration does this represent? How many rotations does the MGR go through from rest until it reaches its operating speed? Note : each rotation represents \( \Delta \theta = 2 \pi ~ ~ (radians) \) One path: \( \theta = \theta_o + \omega_o t + \frac{1}{2}\alpha t^2 \) Another: \( \omega_{avg} = \Delta \theta / \Delta t \) (Sketch a graph of ω vs time.)

 

Relating Angular and Linear Motion

Focus on some point on the object. As the entire object rotates through θ that point moves along an arc of length: l=Rθ Differentiating: dl/dt=Rdθ/dt   or   v=Rω In words: the linear speed of a point on the object along it's circular path is equal to the angular speed of the object multiplied by the distance from the axis of rotation to the point of interest. Note that a point farther out is moving proportionally faster. An object moving in a circle of radius r at a speed v represents a radial acceleration of \[ a_r = \frac{v^2}{r} = \frac{ ( r \omega )^2 }{r} = r \omega^2 \]

 

Example: Merry-go-Round (radial acceleration)
If the MGR has a radius of 4 m and a person is standing on that outer edge: How fast is the person on the outer edge moving when the ride is fully spun up? What is the person's radial acceleration at this point?

 

Tangential Acceleration

What if the object has an angular acceleration (like the MGR during the spin-up)? Arc-length : l=Rθ Differentiating: dl/dt=Rdθ/dt   or   v=Rω Differentiating again: dv/dt=Rdω/dt = Rα This is the linear acceleration of the object along the path, i.e. tangent to the circle the point is tracing out. Referred to as tangential acceleration : at = Rα   The full vector acceleration can thus have both tangential and radial components. (And \( \vec{F}=m\vec{a} \) will need to account for that!)   Note: other common notations you might see:   \( a_{rad} = a_r = a_R \)   \( a_{tan} = a_t = a_T \)

 

Example: Merry-go-Round : tangential and radial acceleration
Find both the tangential and radial components of the acceleration for a person on the outer edge of our Merry-go-Round at these times: The instant after the MGR starts operating (spinning up) The instant just before it reaches its full operating speed The instant just after it has reached its full operating speed and is no longer angularly accelerating.
MGR Angular Velocity:     ω=ωo+αt
Acceleration Components
atan=rα	arad=v2/r = ω2r
Overall Acceleration Magnitude
\[ |a| = \sqrt{ a^2_{tan} + a^2_{rad} } \] (Note the slight 'bump' in the acceleration graph right at the end of the spin-up phase.)

 

Rotational Forces : Torque
Suppose we have bicycle wheel suspended on a stand so that the axle is fixed in place but the wheel can rotate about that point. We then apply the same magnitude of force to various different points on the wheel, and at various angles.
outer edge, radially (no effect) outer edge, tangent to wheel (considerable effect) outer edge but at an angle now: radial component has no effect; only the tangential component change where we apply the force now: move in close to the axis same force but closer in: smaller effect
The angular acceleration is proportional to r (how far out from the axis the force is applied), and is also proportional to the component of the force tangent to the r vector. Define the torque to be τ = Ftan r    (or equivalently: τ=rFtan) Metric units: N · m : (newtons) times (meters) English units: lb · ft : (sometimes seen as ft · lb)   Units Warning:   (force)*(distance) is also the units of work (energy, Joules) Technically, torque and energy have the same units, but: torque is never written as units of Joules. It's always just newton · meters or pound · feet (foot · pounds is usually a unit for work or energy, with pound·feet for torque...)

 

Relating Torque and (Angular) Acceleration: The Moment of Inertia
Consider a point-mass object on a thin (rigid) wire of length L. (One end of the wire is fixed at point Ó .) We apply a vector force F to the object. How does the object move?
Start: Ftan = m atan Morph into something involving rotational variables:     Ftanr = m atan r     but atan = rα and Ftanr = τ so:     τ = ( mr2 ) α
That last equation matches the pattern of Newton's Laws (F=ma) but with rotational entities now (torque and angular acceleration). The proportionality constant (m in Newton's laws) is replaced with something else (here mr2) for the point mass on a wire). That entity is called the moment of inertia which has the symbol I. This same entitiy (moment of inertial) routinely appears in rotational scenarios, so we'll spend a little time looking at it next.

 

Calculating Moment of Inertial (I)
Single Point Mass	Set of Point Masses	Solid Object
\[ I = mr^2 \]	\[ I = \sum m_i r^2_i \]	\[ I = \int r^2 dm \]

 

Rotational Version of Newton's Laws

\[ \sum \tau = I \alpha \] All three of those entities are about a specified axis τ : torque about that axis (N·m) I : moment of inertia about that axis (kg·m2) α : resulting angular acceleration about that same axis (rad/s2) Every force acting on an object also represents a torque acting on the object, with τ=rFtan, where r is the distance from the axis of rotation to the point where that force is being applied to the object.

 

Merry-go-Round (torque)
Earlier, we had a Merry-go-Round that took 6 seconds to spin up from rest to its operating speed, where the final period was 4 seconds. We found the MGR had an angular acceleration of α = π/12 = 0.2618 s-2 . Suppose the MGR has a moment of inertia (for the given axis of rotation) of I = 2500 kg m2 (We'll see where that came from next time.)
What torque must the motor driving the MGR be generating? τ = I α = ? Convert that from N·m to lb·ft Conversion factors: 1 lb = 4.44822 N and 1 m = 3.281 ft Compare this to typical car engine torques, which range from 100 to 400 lb·ft. The Porsche Taycan Turbo S from an earlier example generates up to 774 lb·ft of torque. Is the 6 second spin-up realistic?