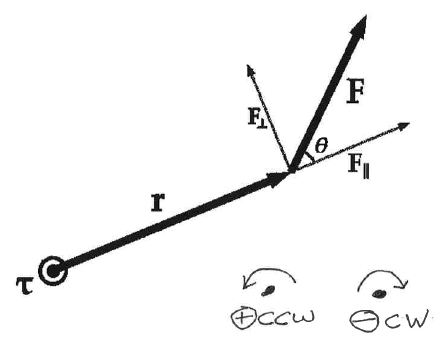
Rotational Kinetic Energy
A rock is flying through the air, and while doing so it's rotating about it's center of mass. How much kinetic energy would the rock have? The rock as a whole is a mass m flying at some (center-of-mass) speed v, so there's the usual kinetic energy of \[ K = \frac{1}{2}mv^2 \] but there's also kinetic energy in the rotation of the object about it's CM.
Getting the rotational part:   Break the object into an infinite number of infinitesimal little mass elements mi.   Each mi mass element is rotating about an axis through the center of mass of the object. Suppose the angular rotation speed (of the entire object) about this axis is ω.   This mi is located ri from the axis of rotation so it is moving in a circle of that radius at an angular speed of ω which represents a speed of vi=riω.
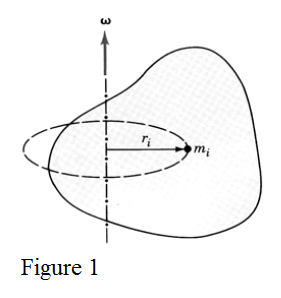
That means each little mi is also contributing an additional kinetic energy of:	\[ K_i = \frac{1}{2}m_i v^2_i \]
which we can write as:	\[ K_i = \frac{1}{2}m_i ( r_i \omega )^2 \]
Expanding:	\[ K_i = \frac{1}{2}m_i r^2_i \omega^2 \]
Summing these over the entire object:	\[ K = \sum K_i = \frac{1}{2} ( \sum m_i r^2_i ) \omega^2 \]
which is just:	\[ K = \sum K_i = \frac{1}{2} I \omega^2 \]
An object can potentially have both types of kinetic energy: \[ K_{cm} = \frac{1}{2} m v^2_{cm} \] \[ K_{rot} = \frac{1}{2} I \omega^2 \] It's total kinetic energy then would be: \[ K = K_{cm} + K_{rot} = \frac{1}{2} m v^2_{cm} + \frac{1}{2}I\omega^2 \] Note: Kcm is sometimes called Ktrans (translational) in some books/fields. Note: if the object is purely rotating (even if the axis doesn't pass through the CM) it's almost always simpler to just treat it as pure rotation with \( K = \frac{1}{2}I \omega^2 \).
Rotational Energy: Flywheels
1-Cylinder Steam Engine Locomotive
Video (long, but the first few seconds shows a steam-powered shop that uses a large flywheel to store energy): video

 

Rotational Work and Power
Rotational Work	\[ W = \tau \Delta \theta \]
Rotational Power: P=(work)/(time)=dW/dt	\[ P = \tau \omega \]

 

Grinding Wheel
A grinding wheel is a uniform cylinder with a radius of 8.50 cm and a mass of 0.380 kg. The motor powering the device spins the grinding wheel up from rest up to 1500 RPM in 0.5 sec.
Calculate: the moment of inertia about its rotation axis the torque the motor must be generating how fast (m/s) is a point on the outer edge moving? the radial acceleration of that point How many revolutions did the wheel rotate through during this spin-up? How much energy is 'stored' in the rotating grinding wheel? What average power must the motor be putting out?

 

Rotational Version of Newton's Laws
\[ \sum \tau = I\alpha \]	with τ, I and α all about a particular axis of rotation
SIGNS: POSITIVE means counter-clockwise about the axis of rotation NEGATIVE means clockwise about that axis
Moment of inertia	\[ I = \sum ( m_i r^2_i ) \hspace{2em} or \hspace{2em} I = \int r^2 dm \]
Rotational kinetic energy	\[ K_{rot} = \frac{1}{2} I \omega^2 \]
Work	\[ W = \tau \Delta \theta \]
Work-K and CoE mathods still work, but:	\[ K = K_{cm}+K_{rot} = \frac{1}{2}mv^2_{cm} + \frac{1}{2}I\omega^2 \]
Power	\[ P_{avg}=(work)/(time) \hspace{1em} and \hspace{1em} P=dW/dt=\tau\omega \]
Angular equations of motion
Angular velocity	\[ \omega = \omega_o + \alpha t \]
Angular position	\[ \theta_o + \omega_{avg} \Delta t \hspace{2em} \theta = \theta_o + \omega_o t + \frac{1}{2} \alpha t^2 \]
Useful shortcut sometimes	\[ \omega^2 = \omega^2_o + 2 \alpha \Delta \theta \]

 

Example: Pulley

A 15 N force is applied to a cord wrapped around a pulley with: mass M = 4 kg outer radius: Router = 33 cm inner radius: Rinner = 3 cm. There is also a frictional torque at the axle of magnitude  |τfriction|=1.1 N m. If the system starts at rest, how fast will the pulley be turning after one complete rotation? (That is, after: Δθ=2π rad.) Work-K:   \( K_{final} = K_{initial} + \sum W \) Kinetic energy here:   \( K_{rot} = \frac{1}{2}I \omega^2 \) 'I' for this geometry:  \( I=\frac{1}{2}M( R^2_{outer} + R^2_{inner}) \) Work:  \( W = \tau \Delta \theta \) Torque:  \( |\tau| = rF_{tan} \) (sign?)

 

Falling Meter Stick

A meter-stick is suspended from one end and can rotate freely about that point. If it's released at rest in position A: What will be the angular speed of the ruler at position B? How fast will the far end of the ruler be moving (in m/s) at position B? Why can we NOT use equations of motion for this one? Use conservation of energy   Model the 'ruler' as a long thin rod of mass M and length L, rotating about one of it's ends. Consulting the table of moments of inertia, we see I = ⅓ML2 for this geometry.

 

Important Detour: Ug for Extended Objects
In a CoE sense here, the stick is changing elevation, but different parts are undergoing different changes. How do we deal with gravitational potential energy for an extended object? If we break the object up into an infinite number of infinitesimal pieces, with h being our vertical axis:	\[ U_g = \sum m_i g h_i \hspace{2em} so: \] \[ U_g = ( \sum m_i h_i) g \hspace{2em} but: \] \[ h_{cm} = ( \sum m_i h_i)/M \hspace{2em} so: \] \[ U_g = Mgh_{cm} \]
The overall gravitational potential energy for an extended object can be found by in effect replacing the object with a single point mass located at the center of mass of the extended object.

 

Rolling without Slipping

When a ball or wheel rolls across a surface (without slipping), we can relate it's translational and rotational velocities.   Top figure: wheel rolling along a sidewalk to the right. It's CM is moving at some speed vcm.   Bottom figure: moving along with the wheel Wheel appears to be just spinning in place, with the sidewalk moving to the left at vcm. The wheel isn't slipping, so the velocity of its outer edge (v=Rω) must be the same as the velocity of the sidewalk, so:   It's center-of-mass speed and it's rotational speed are locked together: vcm = Rω

 

Ball Rolling Down Ramp
A basketball is released (at rest) at the top of a 30o ramp. If it rolls (without slipping) down the ramp, how fast will it be moving after travelling 4 m along the ramp?   Basketball parameters: M=0.65 kg r=23 cm geometry: hollow sphere
Compare to what we would have gotten before treating this as a point mass sliding down a frictionless ramp. What if this were a solid sphere (like a bowling ball)?

 

Additional Example : Stopping a Rotating Bike Wheel

The bike wheel in the figure has a mass of 4 kg and a radius of 0.4 m. (Treat the wheel as a ring where all the mass is at that distance from the axis.) What is the moment of inertia of the wheel for rotations about it's (fixed) axle? The wheel is rotating at 4 rev/sec and we want to bring it to a stop by pushing on it with the palm of our hand. If we push (radially) with F=20 N and the coefficient of kinetic friction between our hand and the rubber tire is μk=0.5, how long will it take to bring the wheel to a stop? Forces acting on wheel: Gravity Friction Pushing Force What torque is each force creating? Remember: \( \tau = rF_{tan} \) so where the force is being applied matters.