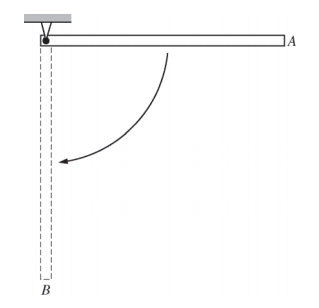
Torque
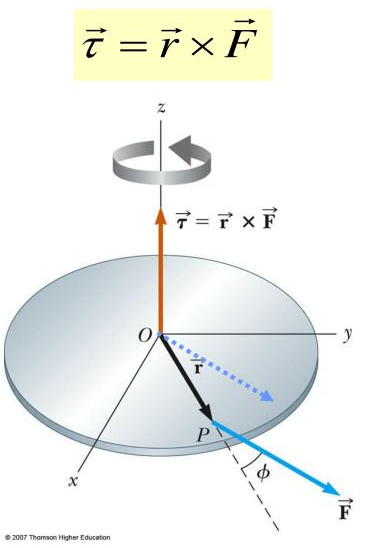
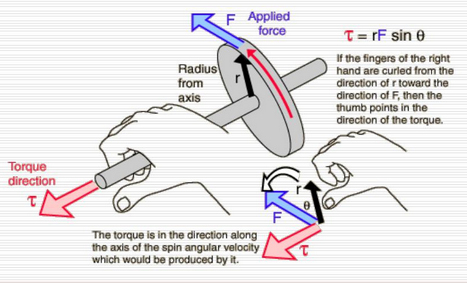
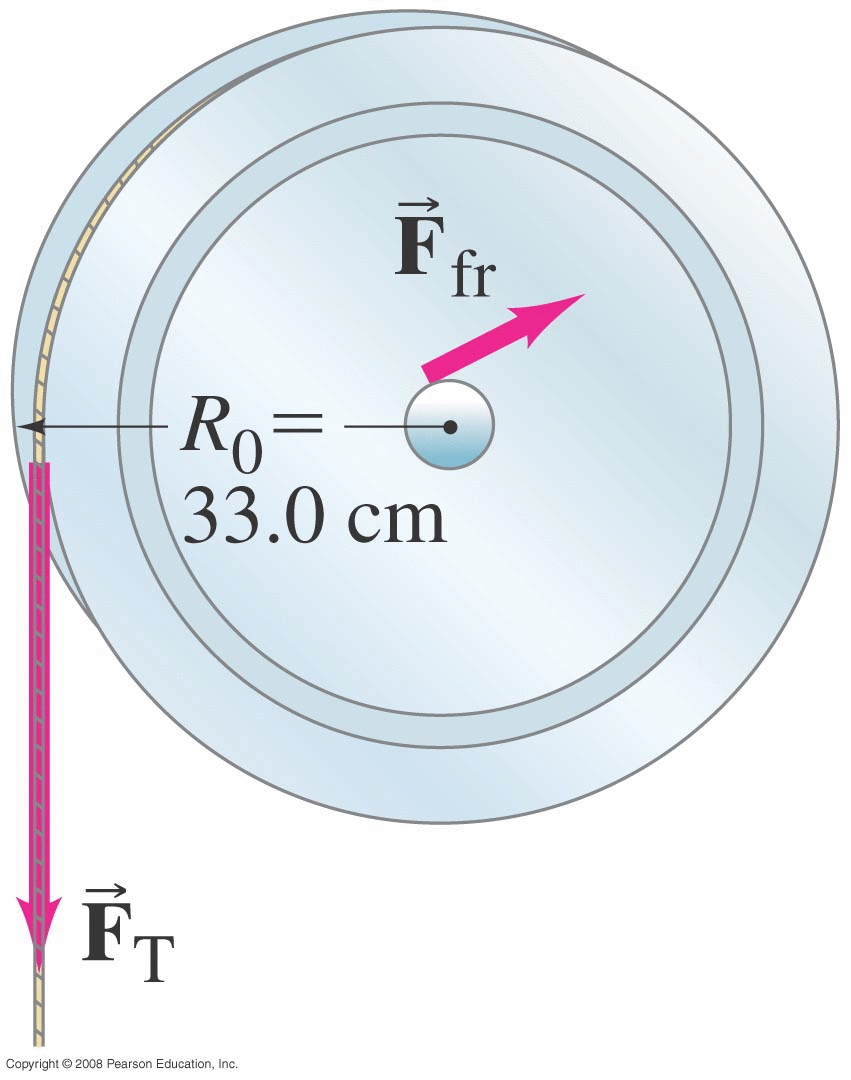
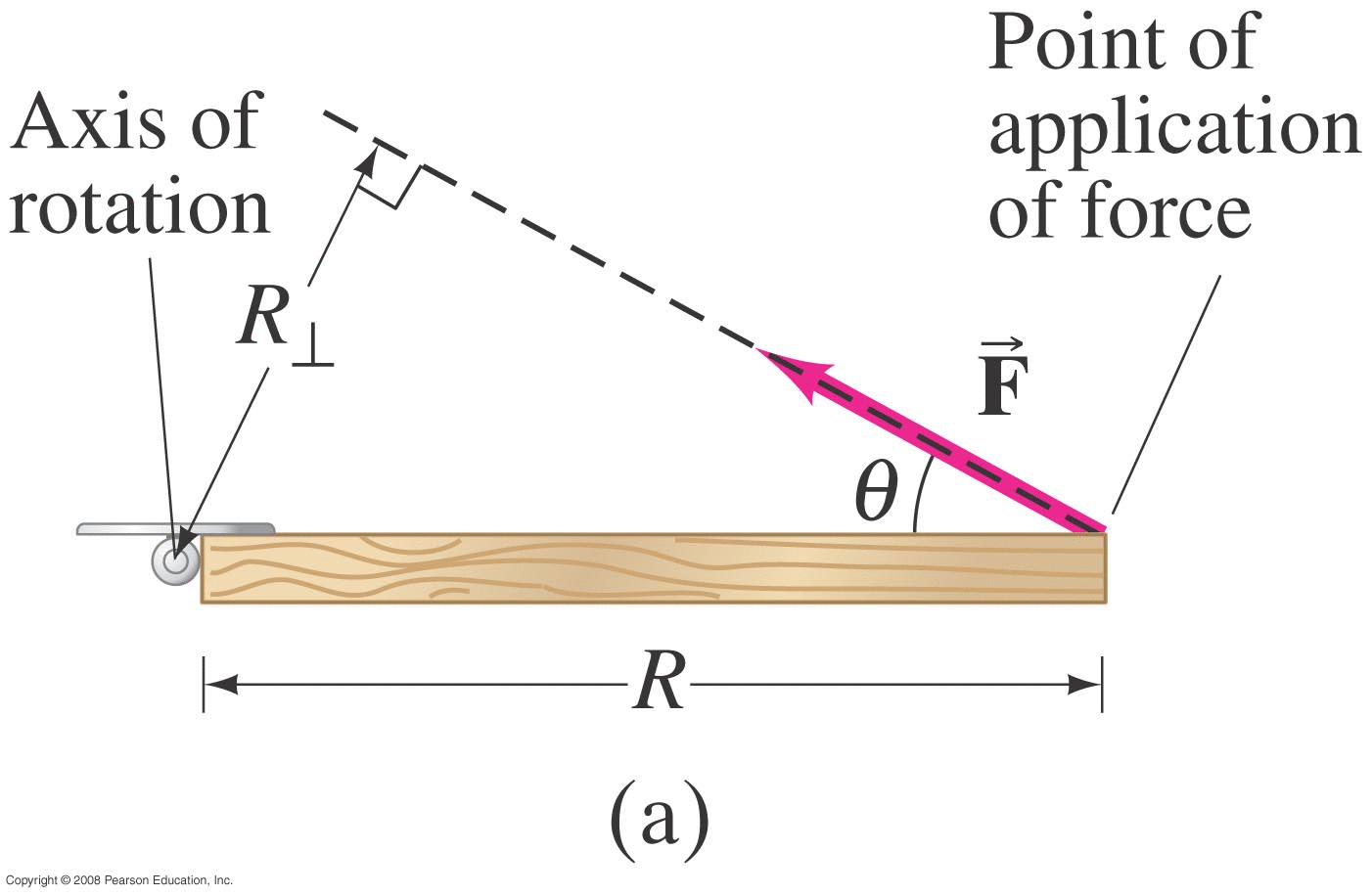
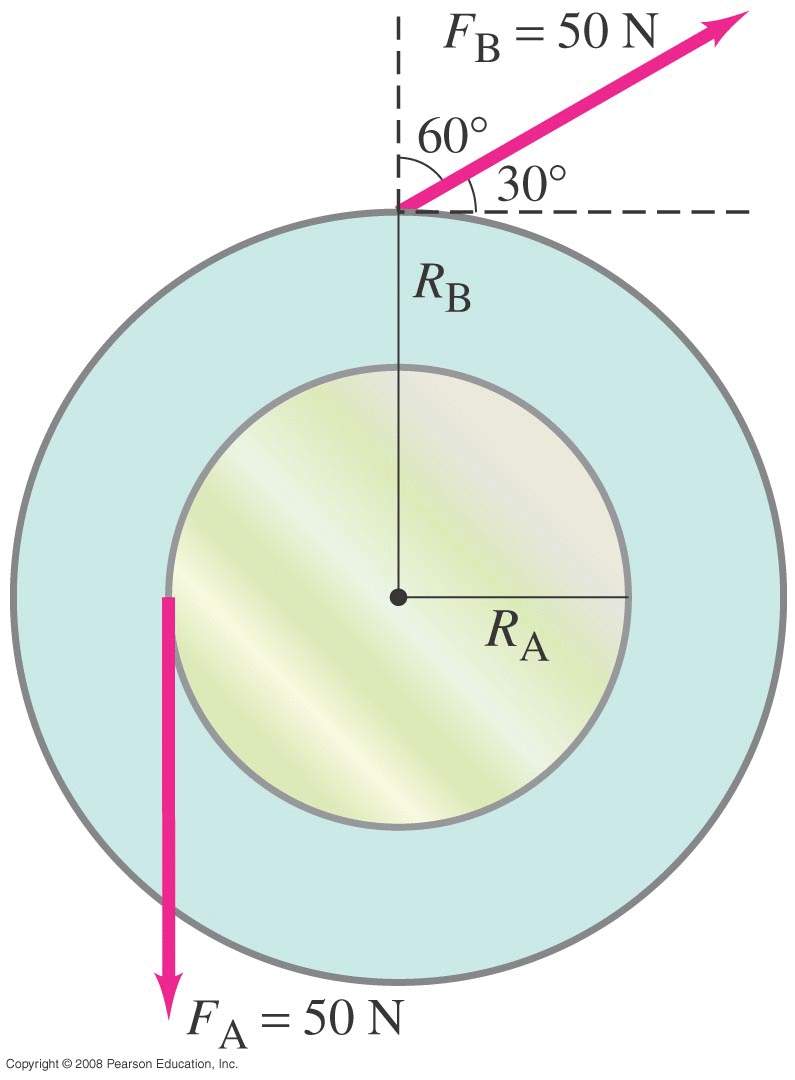
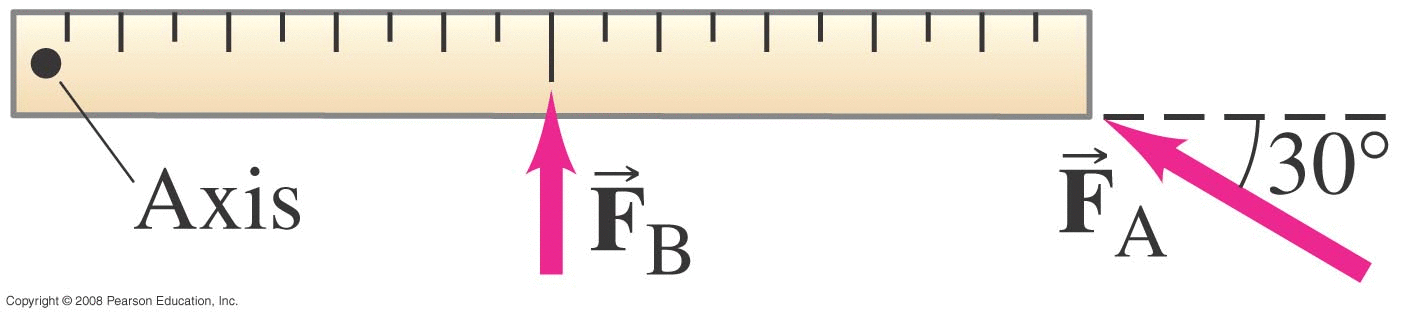
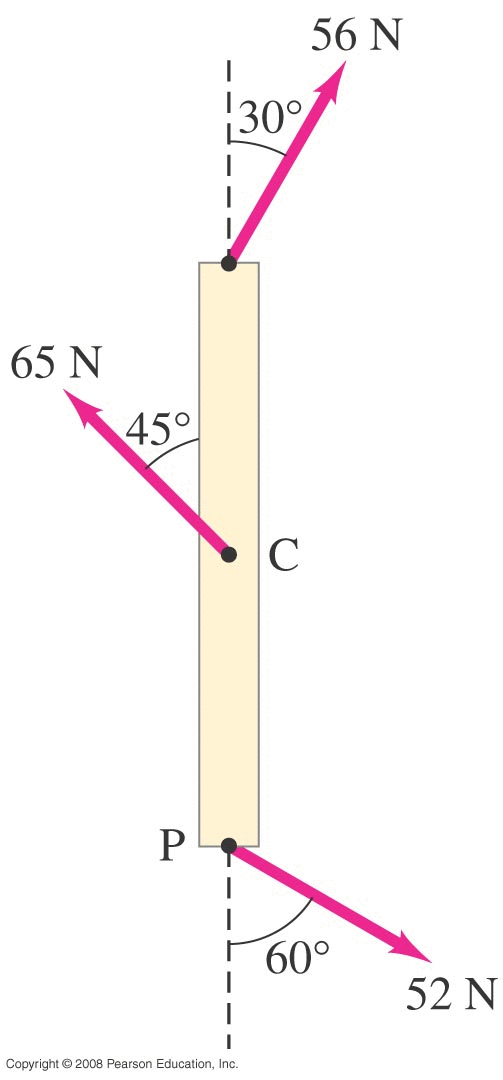
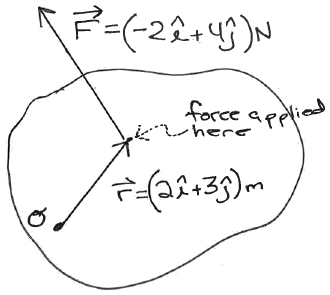
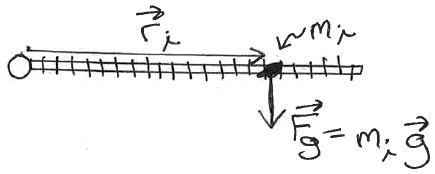
So far, our objects are flat, in the XY plane. They're 'pinned' so they'll rotate about some axis coming up out of the page (Z axis). We apply a vector force F (also in the XY plane) to the object. The vector r points from the axis of rotation to the point where the force is being applied.
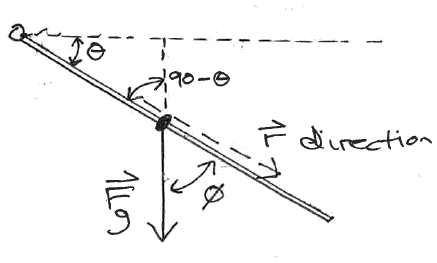
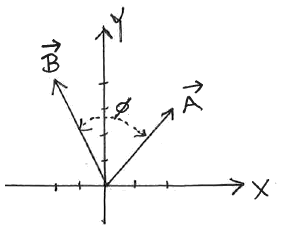
This will create a torque about the axis of: \[ |\tau| = rF_{tan} \] which we can write as: \[ |\tau| = rF\sin{\phi} \] where \( \phi \) is the angle between the directions of the r and F vectors. The sign of τ POSITIVE if this force would induce a counter-clockwise (CCW) rotation NEGATIVE if this force would induce a clockwise (CW) rotation This torque will create an angular acceleration of: \[ \tau = I\alpha \]
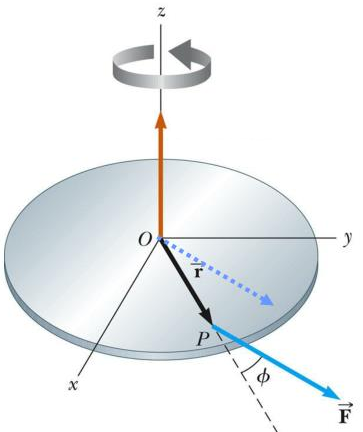
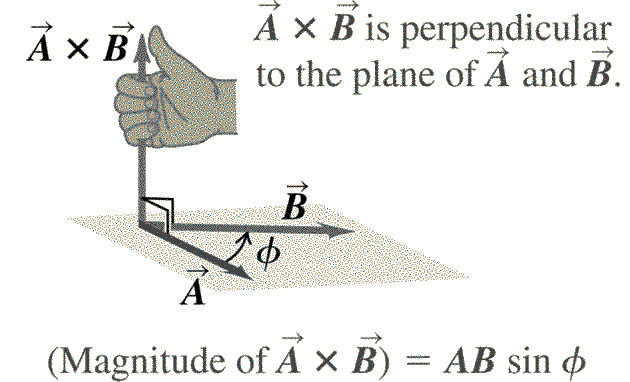
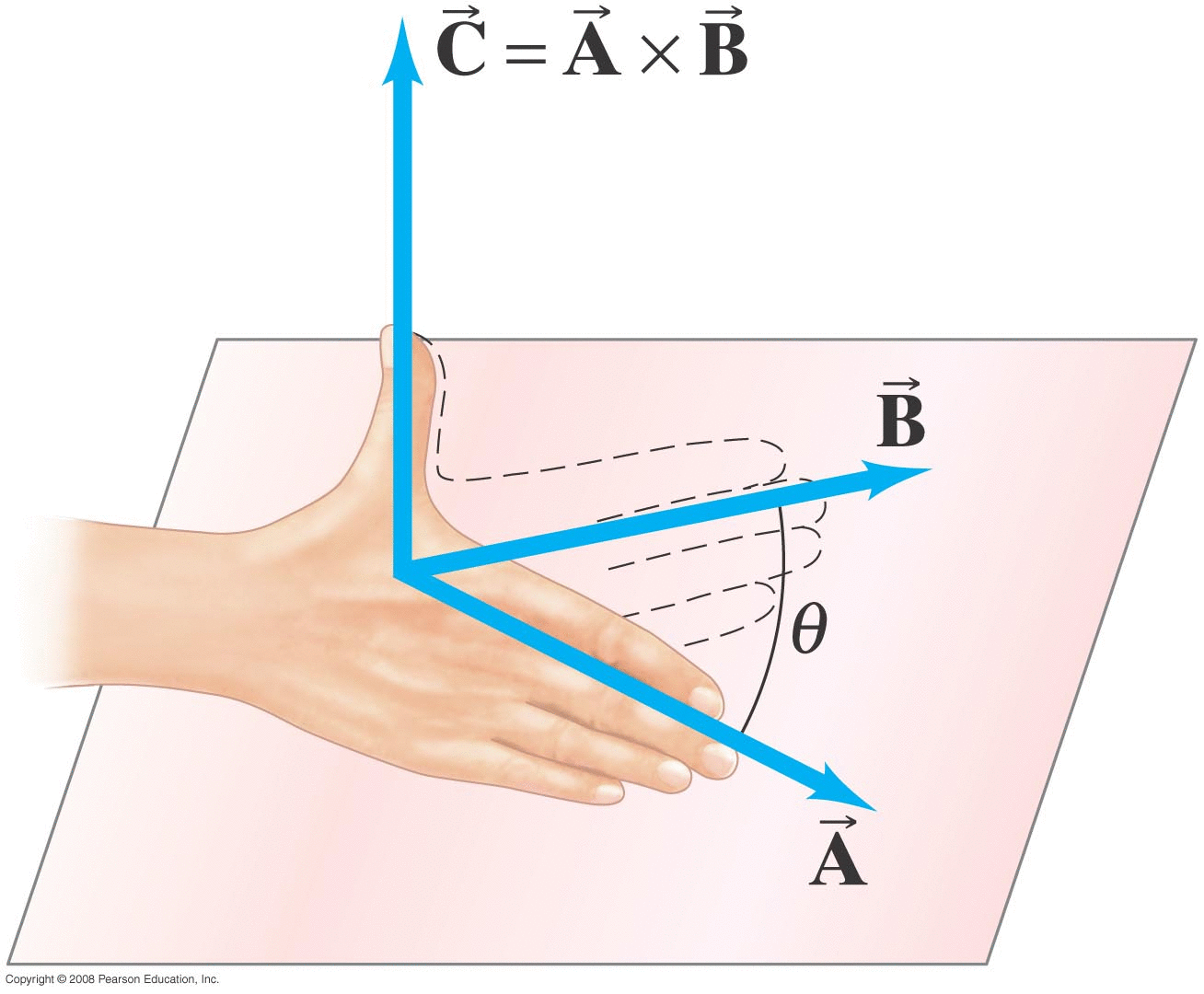
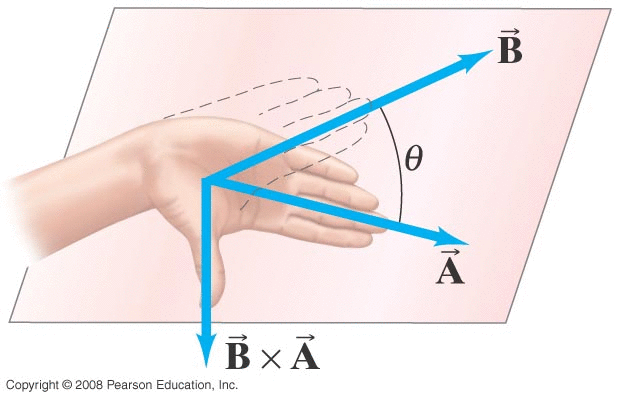
From geometry, any two (non-parallel) lines that intersect define a plane. Here the r and F vectors define a plane and the axis about which rotation will occur is perpendicular to that plane. Is there a math-y way to denote this process: two vectors A and B that combine to create a third vector C that's perpendicular to the plane defined by the first two and has a magnitude of \( C=AB\sin{\phi} \) and the correct direction?

 

Cross Product
The cross product of two vectors: \[ \vec{C} = \vec{A} \times \vec{B} \] creates a vector with these properties: magnitude: ABsin(φ) direction: perpendicular to the plane defined by the A and B vectors, with the direction found using the right-hand rule (starting at the first vector)

WARNING : this type of vector multiplication is anti-commutative: \[ \vec{B} \times \vec{A} = -\vec{A} \times \vec{B} \]

 

Torque as a Cross Product
Compact way of writing torque:	\[ \vec{\tau} = \vec{r} \times \vec{F} \]
(r and F vectors here are in the XY plane)

 

Torque: RHR Sign and Angle Practice
What torque (about the Z axis, coming up out of the page) will each force here be creating?
Each F is being applied tangentially at that point. Router=33 cm     Rinner=3 cm Why is the friction force drawn at an angle in this figure?       (axis at center of disk)	(1) if axis passes through C (2) if axis passes through P

 

Cross Product Example
Determine the cross product A ⨯ B given: \[ \vec{A} = 2\hat{i} + 3\hat{j} \] \[ \vec{B} = -2\hat{i} + 4\hat{j} \] What is the angle between those two vectors?
This isn't just an artificial math example - it would be the exact process we would go through to determine the torque present on some object:
Suppose we have some object that is mounted so that it can rotate about an axis (coming up out of the page at the point labelled O in the figure). A force of: \[ \vec{F} = ( -2\hat{i} + 4\hat{j} )~N \] is applied at a point whose vector location relative to the axis is: \[ \vec{r} = ( 2\hat{i} + 3\hat{j} )~m \] What torque does this create?   \( \tau = \vec{r} \times \vec{F} \) (I'll use this example to illustrate unit vector cross products.)

 

Swinging Meter-stick (again)
A meter-stick is suspended from one end and can rotate freely about that point. If it's released at rest in position A, determine the (initial) angular acceleration of the stick.   We've seen this picture before when we wanted to find the angular speed the meter-stick would have when it reached position B, and use CoE to find that. Here we'll see why we can't solve this problem by using Στ=Iα to find the angular acceleration α and then just use angular equations of motion to find ω. First, what torque is Fg creating here initially? (This is an extended object, so we'll take a short detour first...) How about a little later when the meter-stick has swung through some angle θ?	From table: \( I = \frac{1}{3}ML^2 \) (thin rod rotating about one end)

 

Extended Object: Gravitational Torque
We don't have a point mass here: the mass of the stick is uniformly distributed all along it's length, and each of those mass elements is introducing it's own amount of torque.
Break the object into a large number of tiny pieces of mass mi located at some location \( \mathbf{ \vec{r}_i } \) relative to the axis of rotation. The force of gravity on each little mass element is introducing some torque. What would the total torque due to gravity be here?
We will find that: \[ \vec{\tau}_{gravity} = \vec{r}_{cm} \times (M\vec{g}) \] That is, the torque being created by the object's weight Fg=Mg can be found by pretending that all the object's mass is located at it's center-of-mass point.

 

Swinging Meter-stick (later)
Let's look at the situation a little while later, when the meter stick has rotated through some angle θ. What is the gravitational torque now? We'll find that the torque depends on θ, meaning it isn't constant here. That means the angular acceleration α isn't constant either, taking all our equations of motion off the table. (The only option is how we did this before: CoE, using Krot.)