Electric Dipole
Charges rarely appear alone, so let's look at a particular configuration that appears frequently in molecular interations (i.e. chemistry): the electric dipole where we have two identical but oppositely charges separated by some distance.
Even though the dipole is overall electrically neutral, it will still exert a force on charges nearby, as we'll see.
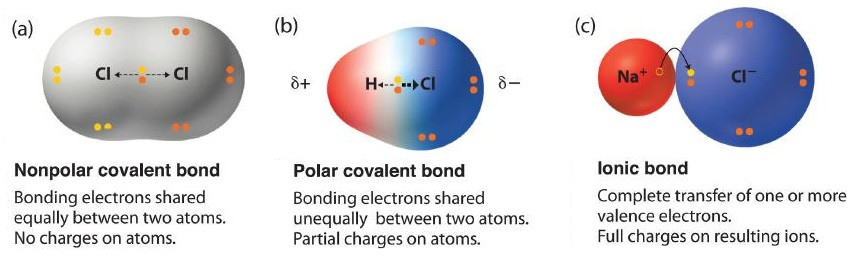
The left figure above shows a model of a chlorine molecule Cl2
Each chlorine atom has 7 of the 8 electrons needed to fill it's outermost shells, and it can 'fix' that by sharing an electron with another atom.
In the middle figure, a chlorine atom is sharing an electron with a hydrogen atom, but looking at the electronegativity chart from the previous lecture, chlorine 'wants' the electron much more than the hydrogen atom. The shared electron here spends more time associated with the chlorine atom than with the hydrogen atom, causing the chlorine 'side' of the molecule to have a slight net negative charge, leaving the hydrogen side of the molecule having a slight net positive charge.
The figure on the right is an even more extreme case. Here we see a NaCl molecule (salt). Again, looking at the electronegativity chart, the difference between sodium and chlorine is very large. Here, the electron isn't really shared, but is removed from the sodium atom and transferred to the chlorine atom, leading to an even clearer dipole character: the Na atom has a net +1e charge, and the Cl atom has a net -1e charge.
Suppose we have charges of +Q and -Q separated by some distance d and we want to find what force those exert on some other charge q that's located some distance x away (along a line that passes through the midpoint between the original charges and is perpendicular to that line; the fancy way of saying this is our new charge q is along the perpendicular bisector.
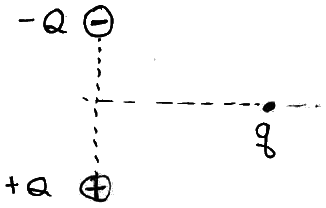
Assuming q is positive, this figure shows the electric force vectors that the +Q and -Q charges will be exerting on it.
The net force acting on q will be the vector sum of those forces.
We'll work through this in class and find there is a net force on that loose charge, and in an unexpected direction...
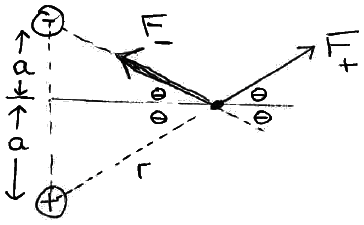
As we move the location of our little test charge 'q', the vector electric forces will change in magnitude and direction.
A useful way of thinking about this is to look at something called the ELECTRIC FIELD.