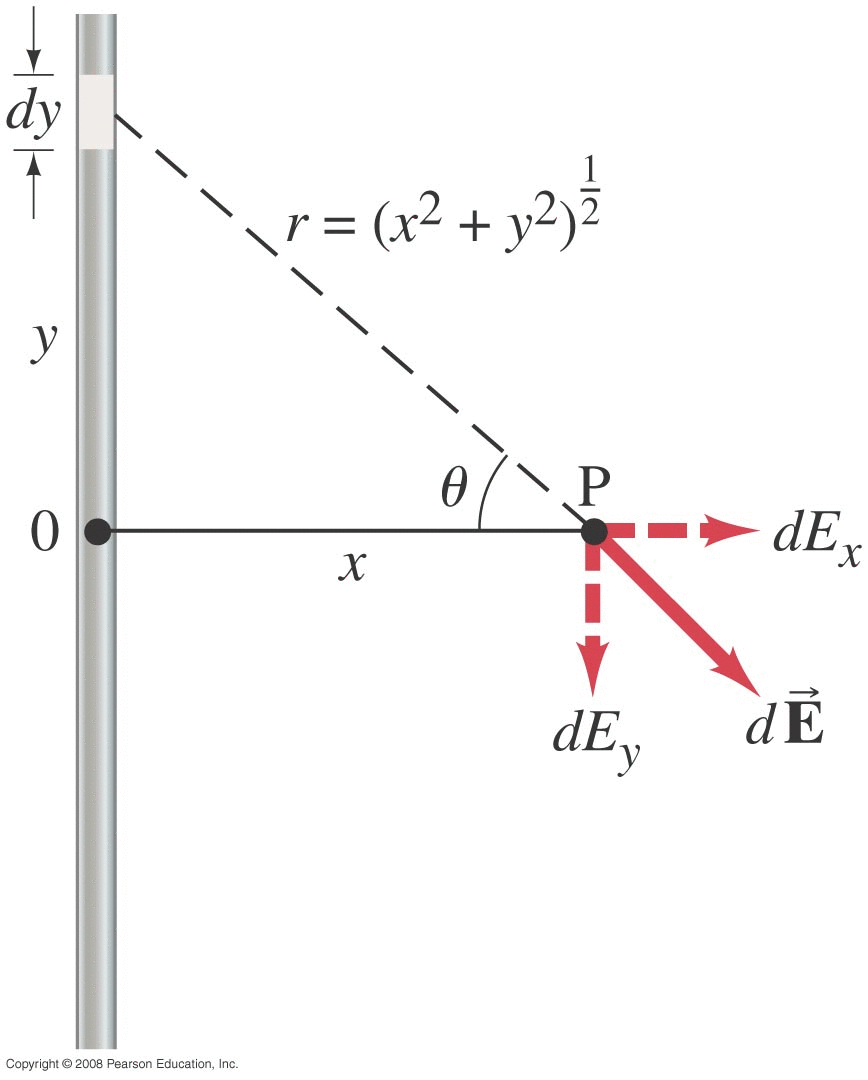
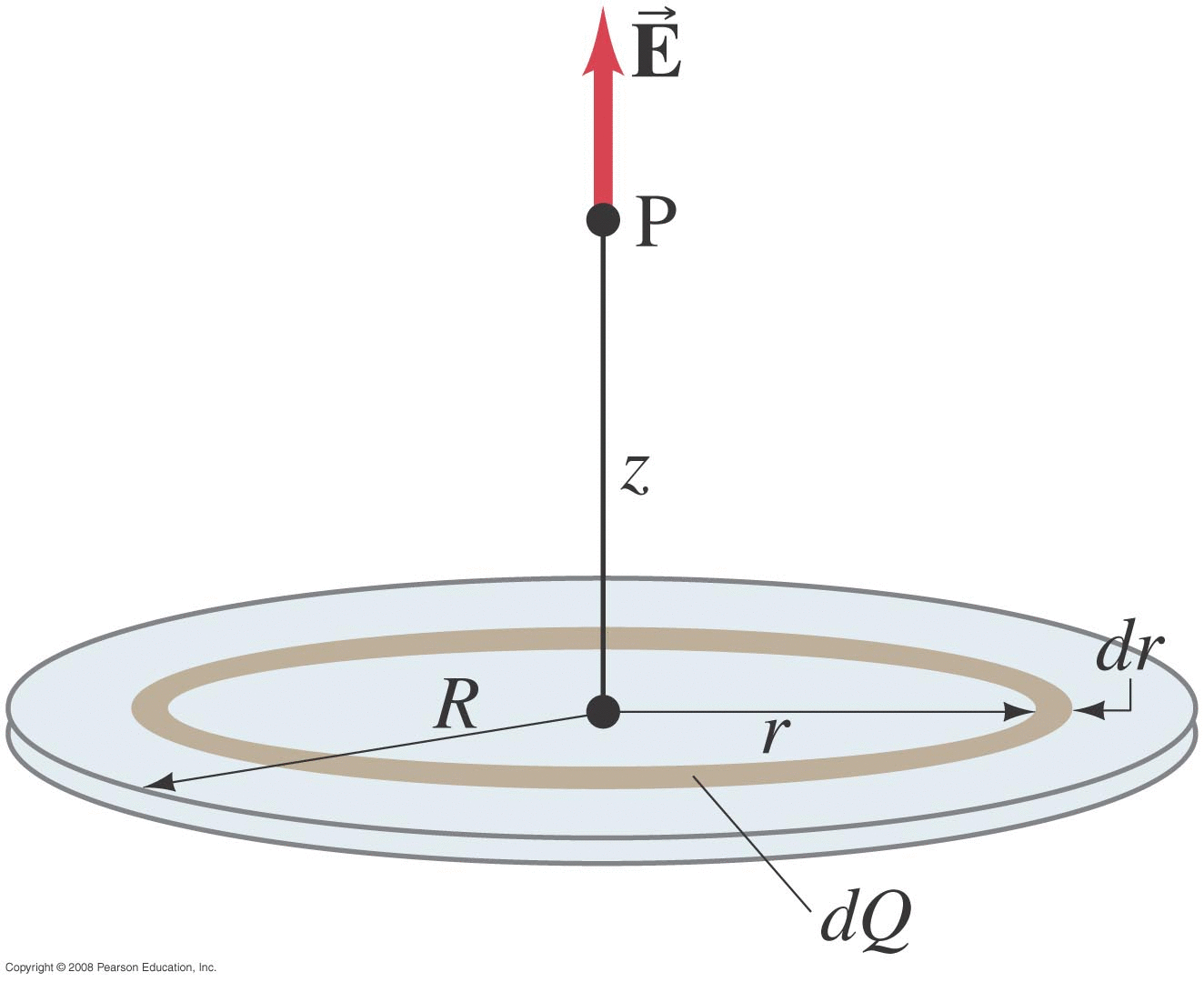
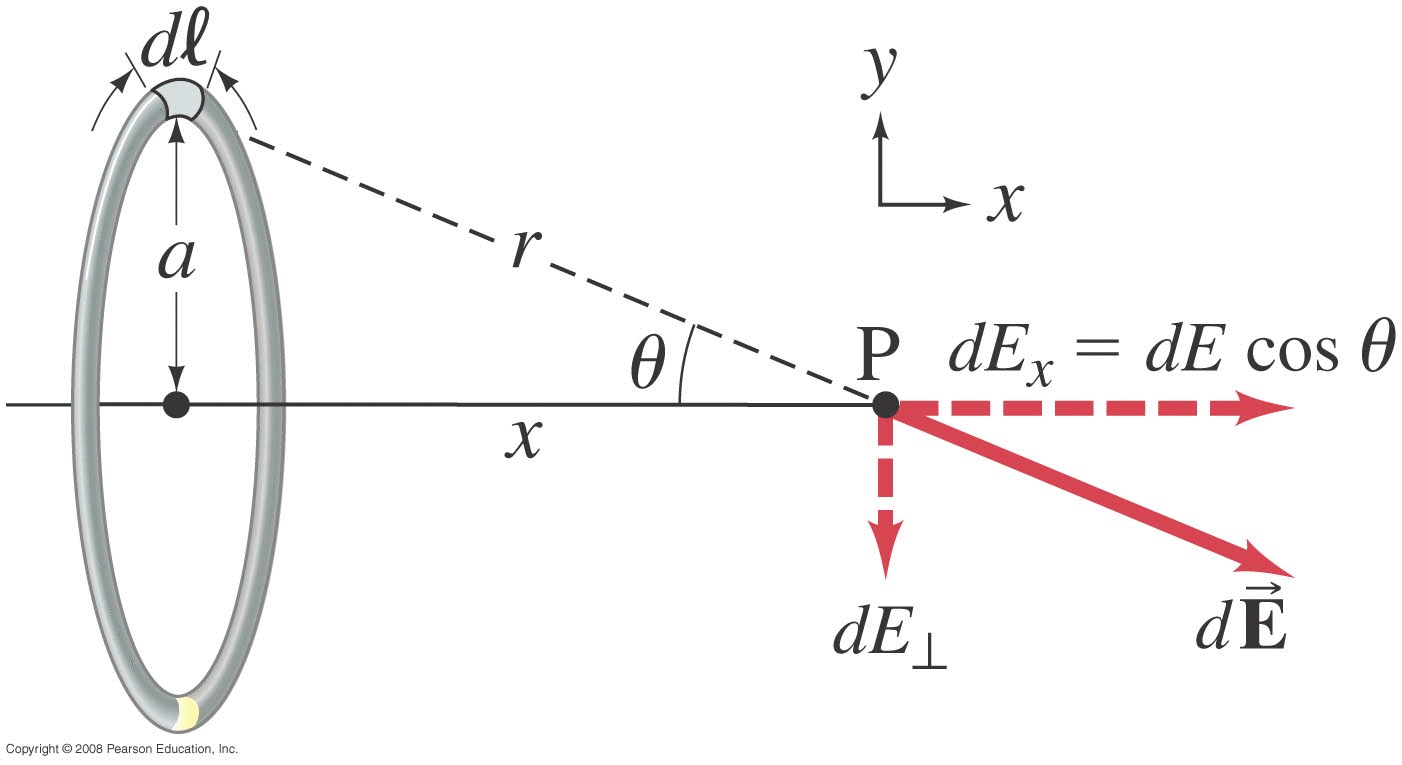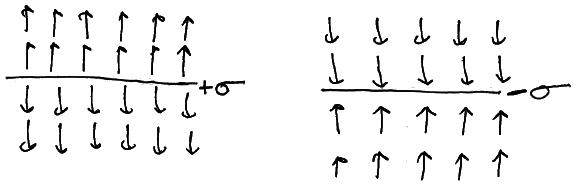Electric Fields around Continuous Charge Distributions
Some geometries we'll be encountering:
Linear and Cylindrical shapes (wires, coaxial cable, ...)	Metal Sheets/plates (variable capacitor from a radio/tv tuner circuit)
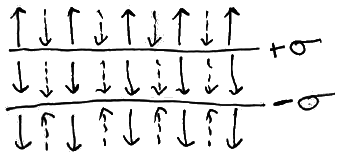
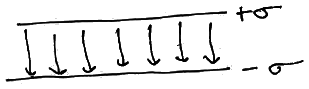
The charge Q will be 'distributed' over the material making up these shapes. We'll encounter various symbols that represent this 'charge density' : ρ represents the charge per volume ( C/m3 ) σ represents the charge per area ( C/m2 ) λ represents the charge per length ( C/m )

 

Infinite Line of Charge

Let λ be the charge in coulombs per meter that's spread along the line. Show that the electric field at some distance 'x' away from the line will be: \( E_x(x) = \frac{ \lambda }{ 2 \pi \epsilon_o x } \) Note that the electric field is dying off as just 1/x instead of the 1/r2 that we had with a point charge.   We've been using k (the Coulomb constant) but another related constant is often encountered: εo, where: \( k = \frac{1}{4\pi \epsilon_o } \) or equivalently: \( \epsilon_o = \frac{1}{4\pi k } \)

 

Ring of Charge
(This one isn't terribly useful on it's own, but we can use this result to calculate E from other distributions.)   Here, we have a total charge of Q, uniformly distributed around a circular ring of radius 'a'.
We'll show that the electric field along a line ('x' in the figure) that runs through the center of the circle, perpendicular to the plane containing the ring is: \( E_x(x) = k \frac{ Qx }{ ( x^2 + a^2 )^{3/2} } \) or in terms of epsilon: \( E_x(x) = \frac{1}{4\pi\epsilon_o} \frac{ Qx }{ ( x^2 + a^2 )^{3/2} } \)

 

Uniformly Charged Disk
Here we have a circular disk of radius 'R', with a charge 'Q' uniformly distributed ('painted') on the disk. The charge density (coulombs per square meter) here will be \( \sigma = \frac{Q}{ \pi R^2 } \)
We'll show that the electric field along a line ('z' in the figure) that runs through the center of the disk, perpendicular to the plane containing the disk is: \( E_z(z) = \frac{\sigma}{ 2\epsilon_o } [ 1 - \frac{z}{ (z^2 + R^2)^{1/2} } ] \)   Note that if we're very close to the disk (or if the radius of the disk is much larger than z, the distance to the point of interest), this reduces to: \( E_z(z) = \frac{ \sigma }{ 2 \epsilon_o } \) which is constant.

Pair of Oppositely Charged Disks
The figures below show disks of charge that we're looking at edge-on. The positive disk has electric field lines of magnitude \( E = \frac{\sigma}{2\epsilon_o} \) directed away from the disk (upward on the top, downward from the bottom). The negative disk has electric field lines of the same magnitude but directed in towards the disk. What happens if we place the positive disk just above the negative one. The solid lines show the field the +σ disk is creating and the dotted lines show the field the -σ disk is creating. Note that the field strength is doubled between the plates and is ZERO outside of them. This geometry can be used to create very strong but isolated electric fields (and represents an electronic device called a capacitor).

Motion of Charged Particles in Electric Fields Example: electron accelerating in the Earth's electric field

The bottom right picture above represents our reality here near the surface of the Earth, where there's an electric field pointing downward with a magnitude of (very roughly) 150 N/C. It varies dramatically from this value depending on whether you're on land or water, what the weather conditions are and so on, but that's a reasonable overall average value. The parking-lot side of Hilbun is about 15 m from the ground to the roof. If we drop an object (at rest) from the roof, the force of gravity will accelerate the object downward and it will reach the ground moving at about 17 m/s. When the object hits the ground, friction may release some electrons. How fast would those electrons be moving upward by the time they reach the level of the roof? Charge on the electron: \( q = -1e = -1.602 \times 10^{-19}~C \) Mass of the electron: \( m_e = 9.11 \times 10^{-31}~kg \)