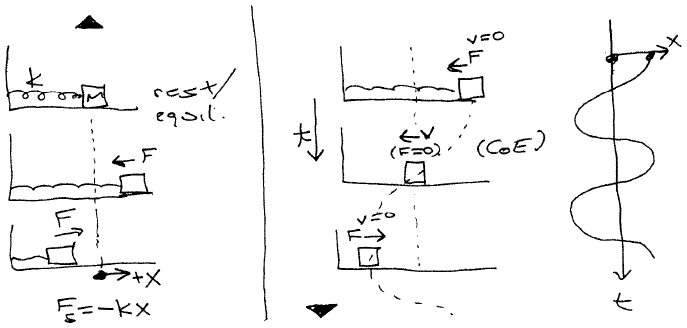
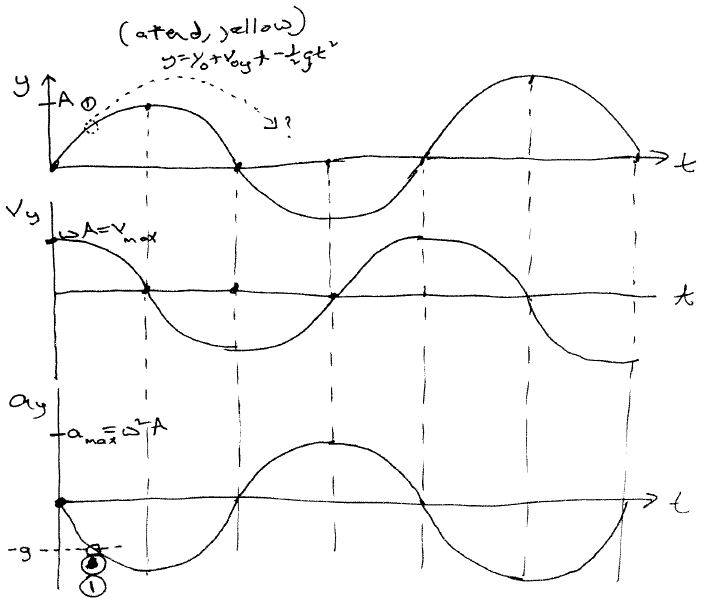
14.1 : Oscillations - Mass on a Spring (Lab 1)

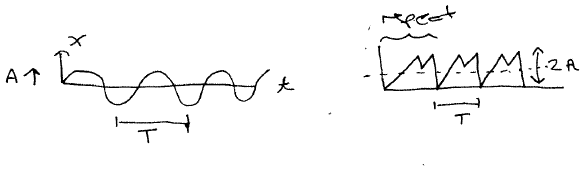
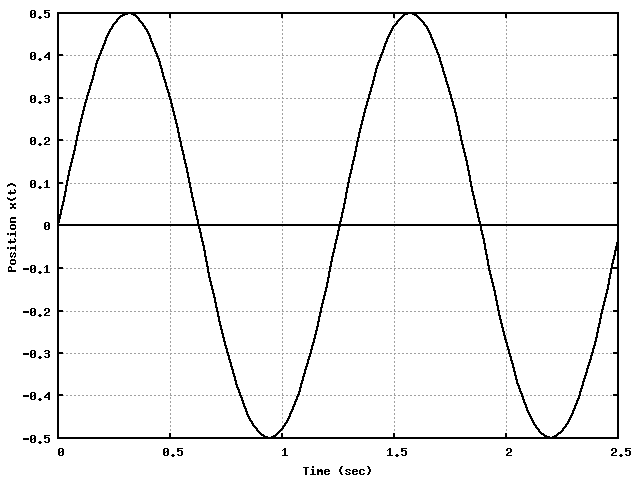
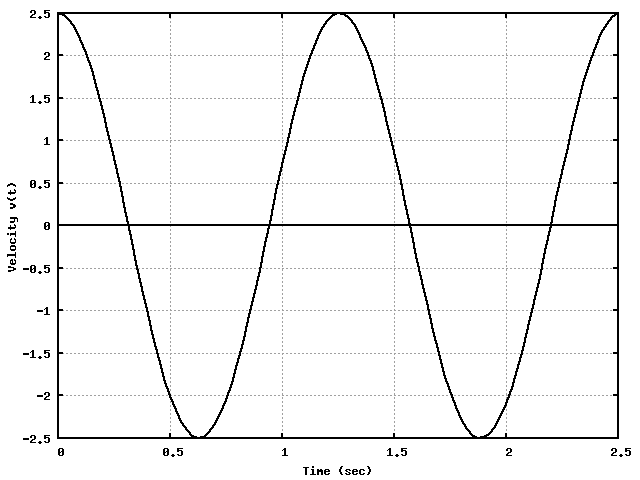
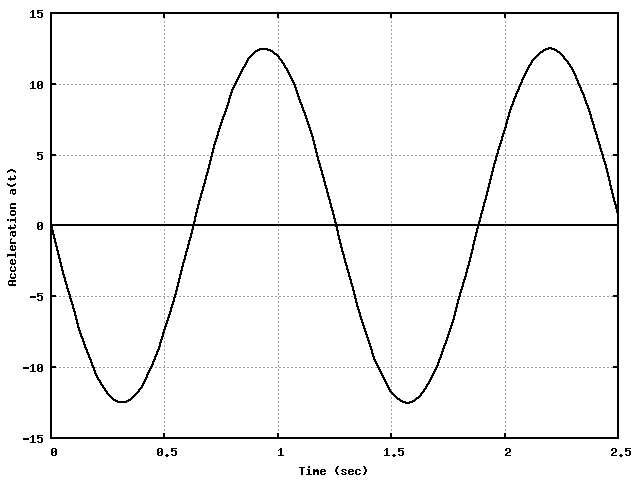
Periodic motion : some definitions, symbols and conventions:   Definitions Amplitude : A cycle Period (time per cycle) : T Frequency (cycles per time) : f=1/T Angular frequency ω = 2 π f = 2 π / T Conventions A, T, f, ω generally taken to be POSITIVE Example: x(t) = -2 sin(-3t)   vs   x(t) = 2 sin(3t)

 

Linear Restoring Forces : Mass on a Spring

Linear restoring force: F(x) = -kx Apply Newton's Laws: F=ma=md2x/dt2 Resulting differential equation \[ \hspace{2em} \frac{d^2x}{dt^2} = -\frac{k}{m}x \] Solutions? General solution: x(t) = A cos( ωt + φ ) where ω2 = k/m

 

Example 1
Suppose we let a 2 kg mass oscillate on a spring of unknown spring constant k. We record a few cycles of data and find that it's position can be written as: \[ x(t) = 0.5\cos{ ( 5t-\pi/2 ) } \] (with all units in standard metric: meters, rad/s, etc).		Position (m)
Let's extract everything conceivable about this motion : period, amplitude, frequency, spring constant, initial position and velocity, acceleration, maximum velocity, maximum acceleration, etc Differentiating the expression we have for x(t) yields: \[ v(t) = dx/dt = -2.5\sin{ ( 5t - \pi/2 ) } \] and \[ a(t) = dv/dt = -12.5\cos{ ( 5t - \pi/2 ) } \] We'll do that symbolically to find that: vmax = Aω amax = Aω2
Position (m)	Velocity (m/s)	Acceleration (m/s2

     

 

Example 2
Suppose we have a large diesel generator designed to create 60 Hz AC voltage. Recall from PH2223 that we can create an AC voltage by changing the magnetic flux, either by rotating coils of wire through a magnetic field, or rotating the magnet itself. Either way, something very heavy is rotating and unless everything is perfectly balanced, the machine is likely to vibrate.
We don't want the generator to migrate across the floor like a washing machine or dryer, so we bolt the machine to the floor. The machine is still unbalanced but now it will cause the floor itself to vibrate slightly. Suppose the floor near the machine is oscillating up and down at f=60 Hz with an amplitude of just 1 millimeter. What side effects will this vibration have on other items sitting on the floor (nearby machines, people, etc)?