15.1 : Characteristics of Wave Motion
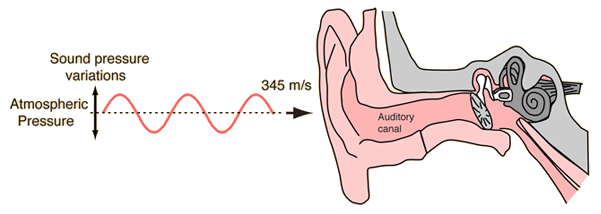
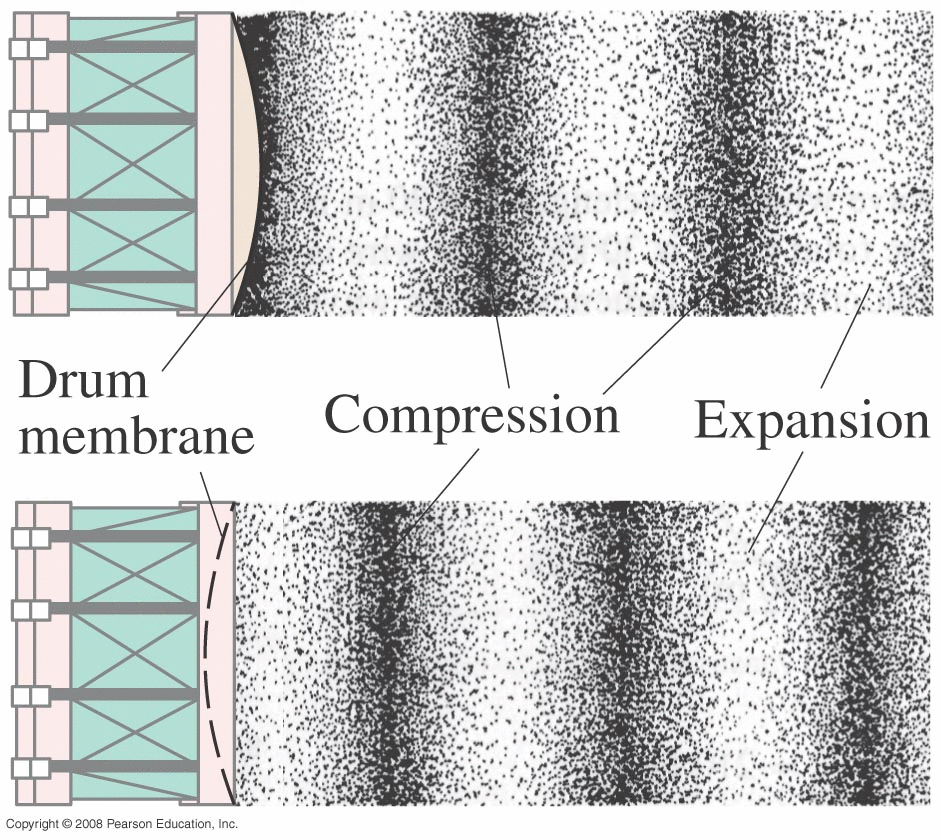
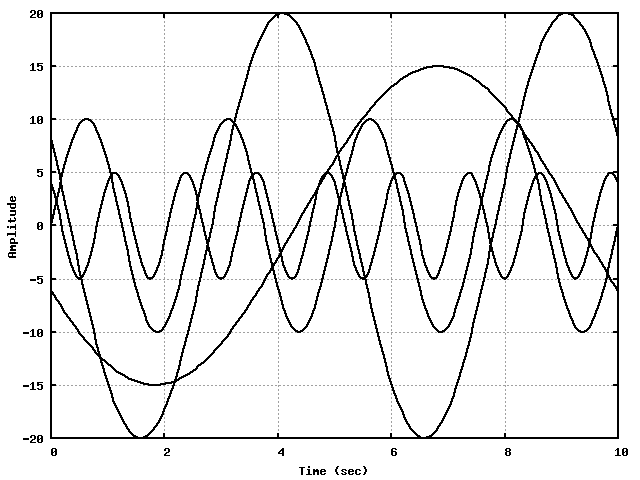
Waves are a common form of periodic motion where a disturbance propagates through a material: ripples on water, sound (which we'll see is tiny pressure fluctuations propagating through the air or some other medium), etc.
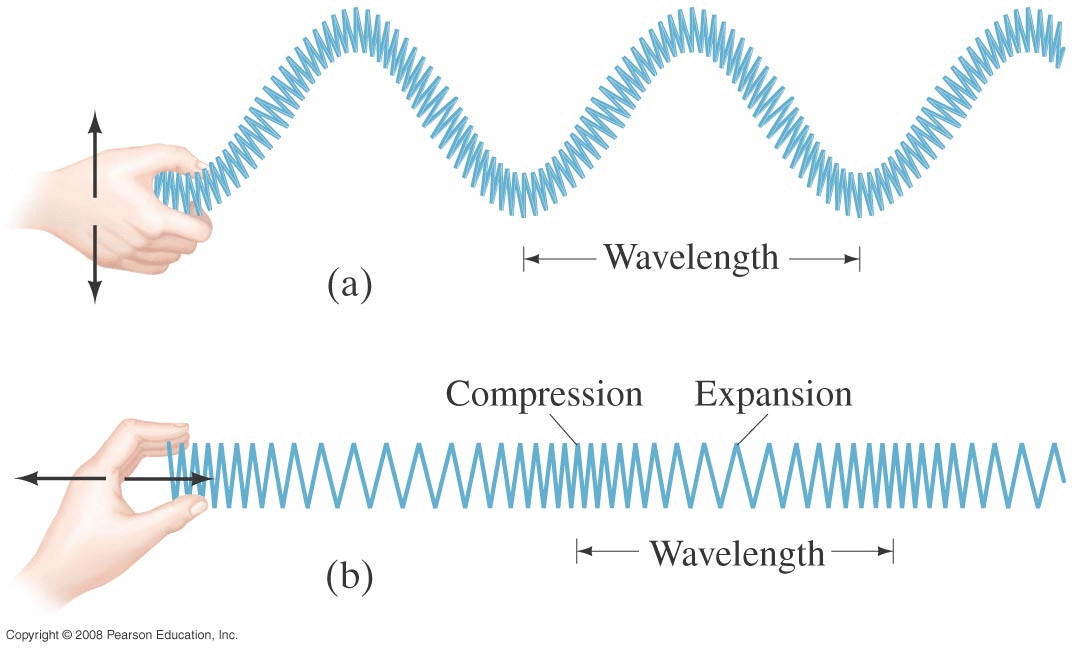
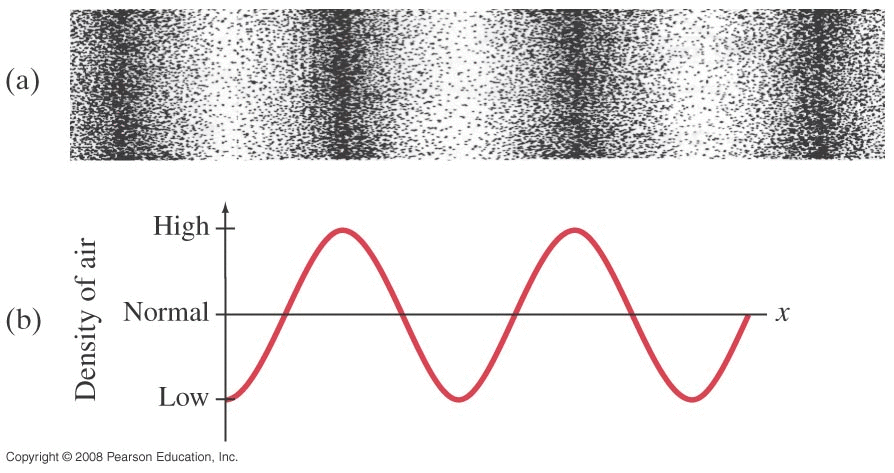
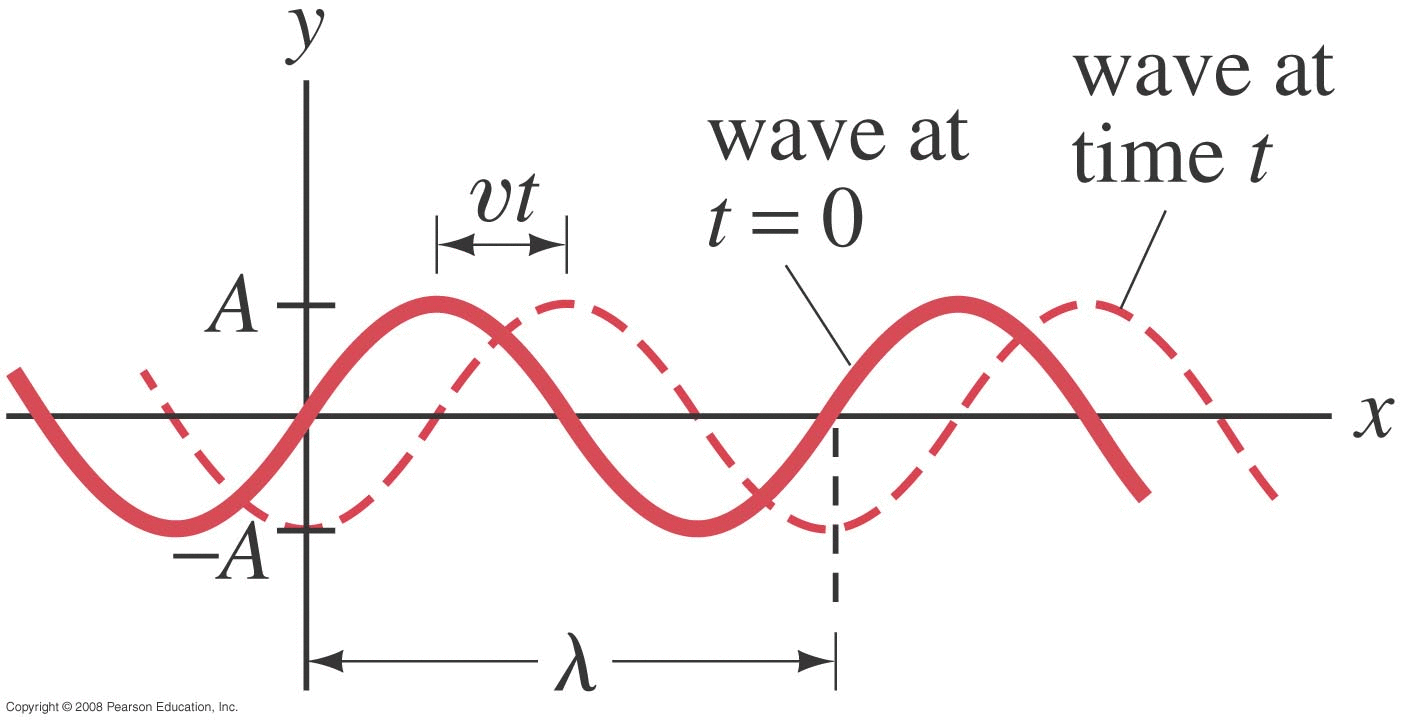
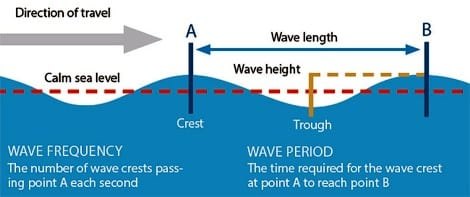
Whether the wave is a nice sine/cosine shape or something else, we can define some parameters similar to what we had in simple harmonic motion in the previous chapter.
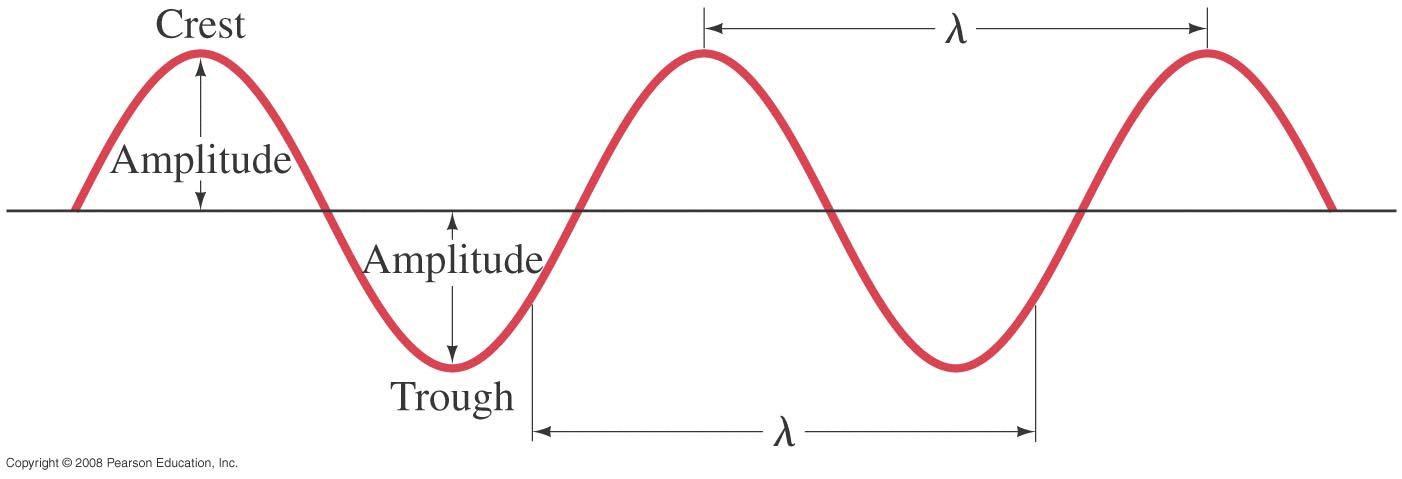
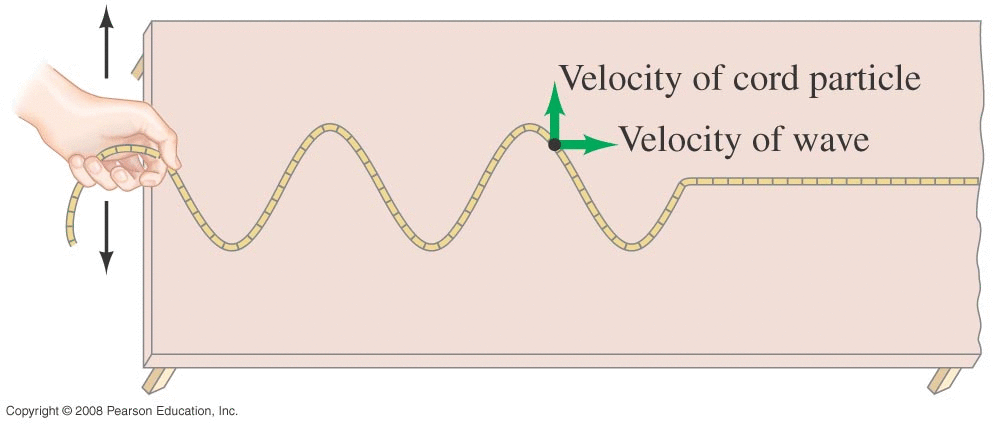
As this sinusoidal shape propagates off to the right, we see that one wavelength will pass by a given point in one period of time. We can thus define a wave speed of v = λ/T .   Each fragment of the material just oscillates up and down (or back and forth, or some combination of those motions), so it's own (oscillating) velocity is entirely different from the overall wave speed itself.

 

Example : Tsunami Wave
Back in 2004 an earthquake caused a significant vertical displacement of the seafloor, which in turn generates a very large and destructive tsunami. Satellites with radar observed the wavelength of the disturbance to be about 800 km and the period was about 1 hour (while the wave was still in the deep ocean). Determine the speed of these waves in deep water.
Example : Human Hearing
The ear nominally responds to sound frequencies from 20 Hz to 20,000 Hz (that range typically shrinks with age - I really can't hear anything above about 4000 Hz ... ). The speed of sound in air is about 343 m/s, so what wavelengths does this range represent?
Example : Radio Waves
The campus radio station WMSV broadcasts at a frequency of f = 91.1 MHz.   Radio signals travel at the speed of light, so     v=c=3*108 m/s.   What is the wavelength of these radio waves?

 

15.2 : Types of Waves
Two particularly common types of waves are: Transverse waves     also known as SHEAR or S-waves   Longitudinal waves     also known as PRESSURE or P-waves
TRANSVERSE WAVES : present in stringed musical instruments (piano, guitar, etc), but also can be present in earthquakes.   LONGITUDINAL WAVES : present in earthquakes too and are how sound propagates through gases, liquids, and solids. They're the type of waves present in wind instruments (trumpet, flute, tuba, organ, etc).   The figure below illustrates sound P-waves being generated by a drumhead oscillating rapidly back and forth:
Why is this difference important?
Each of these wave types, since they represent different mechanics at the molecular level, can propagate at quite different speeds. The chart on the right shows wave speeds in various different rock types (in km/s). The speed for P-waves tends to be much higher than S-waves in pretty much any real-world material.

 

15.4 : Mathematical Representation of a Traveling Wave
We'll mostly be using a fairly simple sine function to represent traveling waves. This process shows how more complicated wave shapes can be constructed via a sum of several/many such sine waves.
Time Series	The four sines that created it.
Amplitudes	Phase Shifts
The mathematical process of converting a time series into the set of wavelengths, amplitudes and phases of the underlying sine/cosine waves is called the Fourier Transform. \[ f(t) = \int^\infty_{-\infty} \hat{f}(\omega) e^{+i \omega t} d\omega \hspace{2em} where \hspace{2em} \hat{f}(\omega) = \int^\infty_{-\infty} f(t) e^{-i \omega t} dt \] (requires continuous, differentiable, integrable...) (related finite sum version for sampled time series...)   You may have run into this in the context of music.   Many frequencies are involved, but if we average the amplitudes over various ranges of frequencies, the spectrum of the music can be displayed.
Your music player may have a display like this in the context of the equalizer settings, where you can boost or suppress various ranges of frequencies. Some music players go further by altering phases and amplitudes in an attempt to simulate what the music might sound like in different environments. (Note: the amplitude scale here is in units of decibels, a logarithmic scale that we'll deal with in the next chapter.)

 

Now that we've justified things a bit, let's look at how we can mathematically represent a propagating sine wave. The bold line represents what the wave looks like at t=0 and the wave here is bodily moving to the right at a wavespeed of v. The dotted line shows what the disturbance looks like at some later time t, when the wave has moved to the right a distance of d=vt.
We'll use this to introduce the concept of a wave number and end up producing a wave function form that describes the moving wave, giving it's amplitude at 'any' point in space or time. \[ D(x,t) = A\sin{ ( kx - \omega t ) } \] An actual wave would consist of many wavelengths and frequencies, so would be represented as a sum of many such terms with varying k and ω values (like the sum of sine waves that represent voice or music). BUT: v=λ/T but ω=2π/T and k=2π/λ so v=ω/k also. For many types of waves, the wave speed is constant and doesn't depend on the wavelength or frequency, so k and ω aren't independent variables. Sound (in air) and light (in a vacuum, and mostly in air) are such waves, so arbitrary wave shapes can be constructed by just varying A and ω. (Fourier synthesis)

 

Example: Tsunami Wave

Recall the tsunami wave we started with, passing under a boat out in the deep ocean.     The amplitude of the wave (in deep water) was A = 1 m. The wavelength was λ = 800 km = 800,000 m The period was T = 1 hr = 3600 s Determine the wave number k and angular frequency ω of the wave. Use that to determine the wave speed. (Verify it's the same as we got before.) As the wave passes under the boat, it (the boat) will move up and down matching the amplitude of the wave (given by the D(x,t) wave function). What vertical velocities and accelerations will the boat experience? (Would they even be aware this wave had passed under them?)