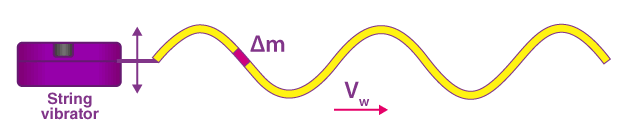
Wave Speed
If you make some simplified assumptions about what's going on down at the micro-level, we can derive expressions for the wave speed in various materials. I'll do one of these (the least obtuse) in class. In each case, we'll find that (within reason) the wave speed v only depends on physical properties of the material but doesn't depend on the amplitude or frequency of the wave. (That turns out to be not entirely correct, as we'll see later with light.)
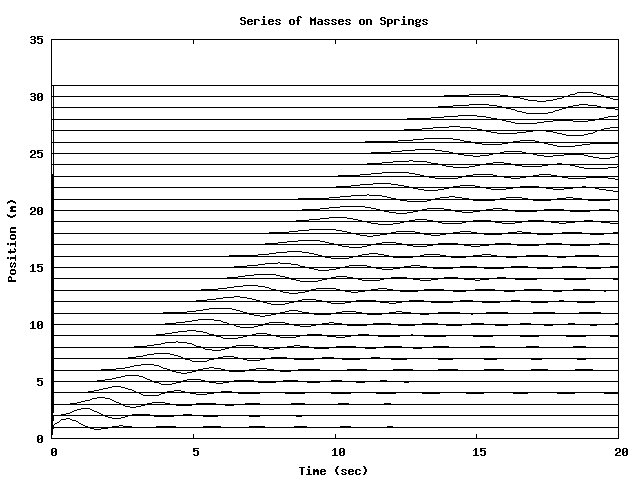
What does wave speed represent? Consider a series of little masses in a line, connected by springs between them. If we disturb a mass on one end, it takes time for that disturbance to reach the other masses:
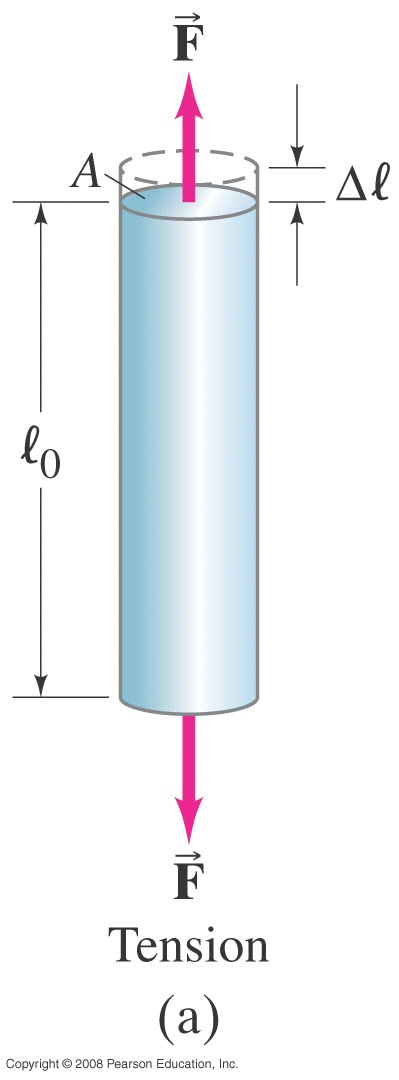
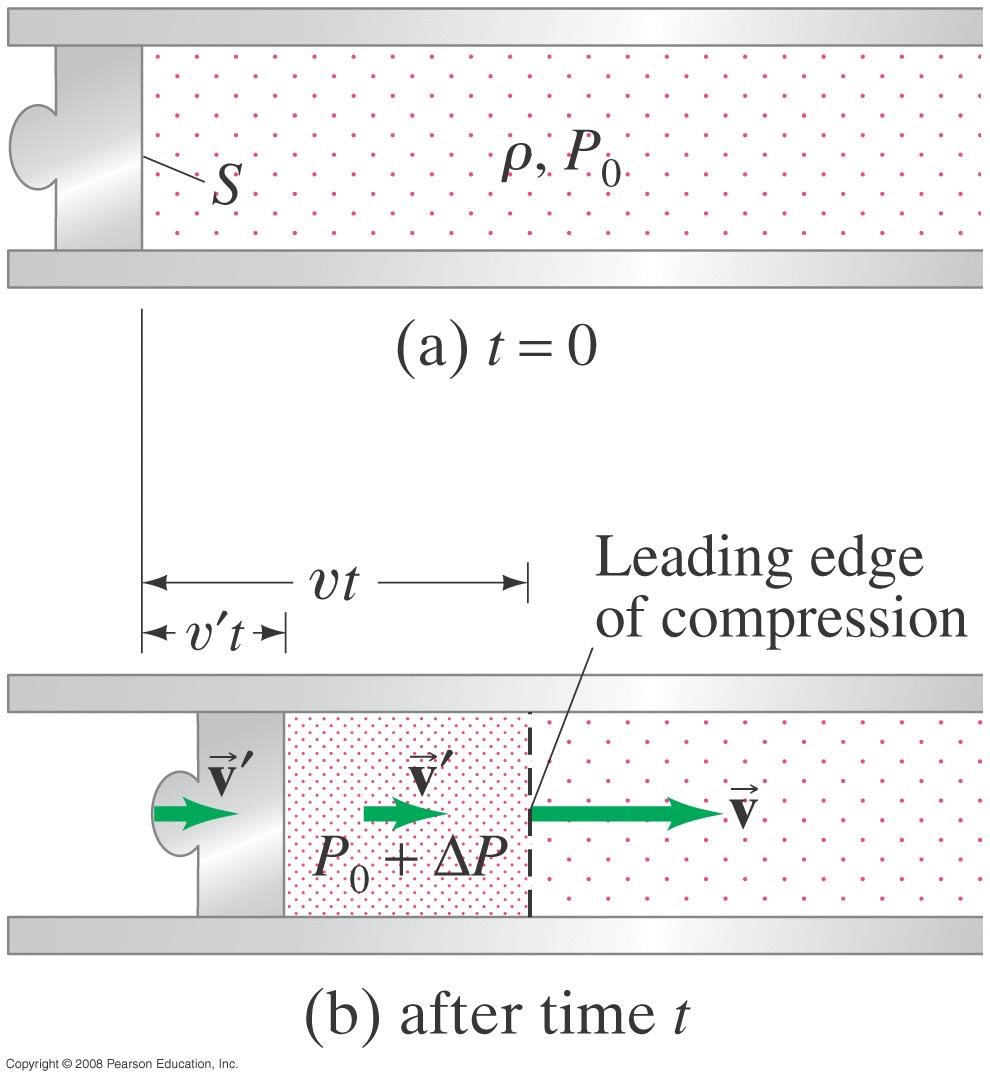
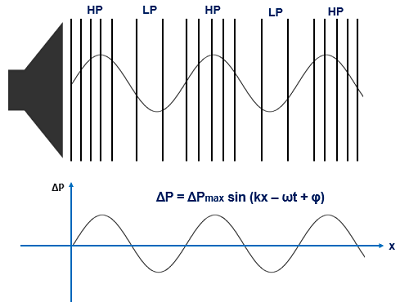
Symbols:     S : cross-sectional area of piston     ρ : density of medium     Po : ambient pressure     P = Po + Δ P : pressure induced by piston     v' : piston velocity     v : wave speed     dashed line : leading edge of compression
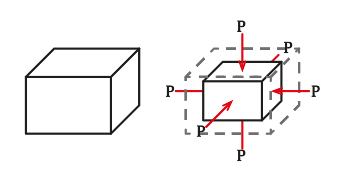
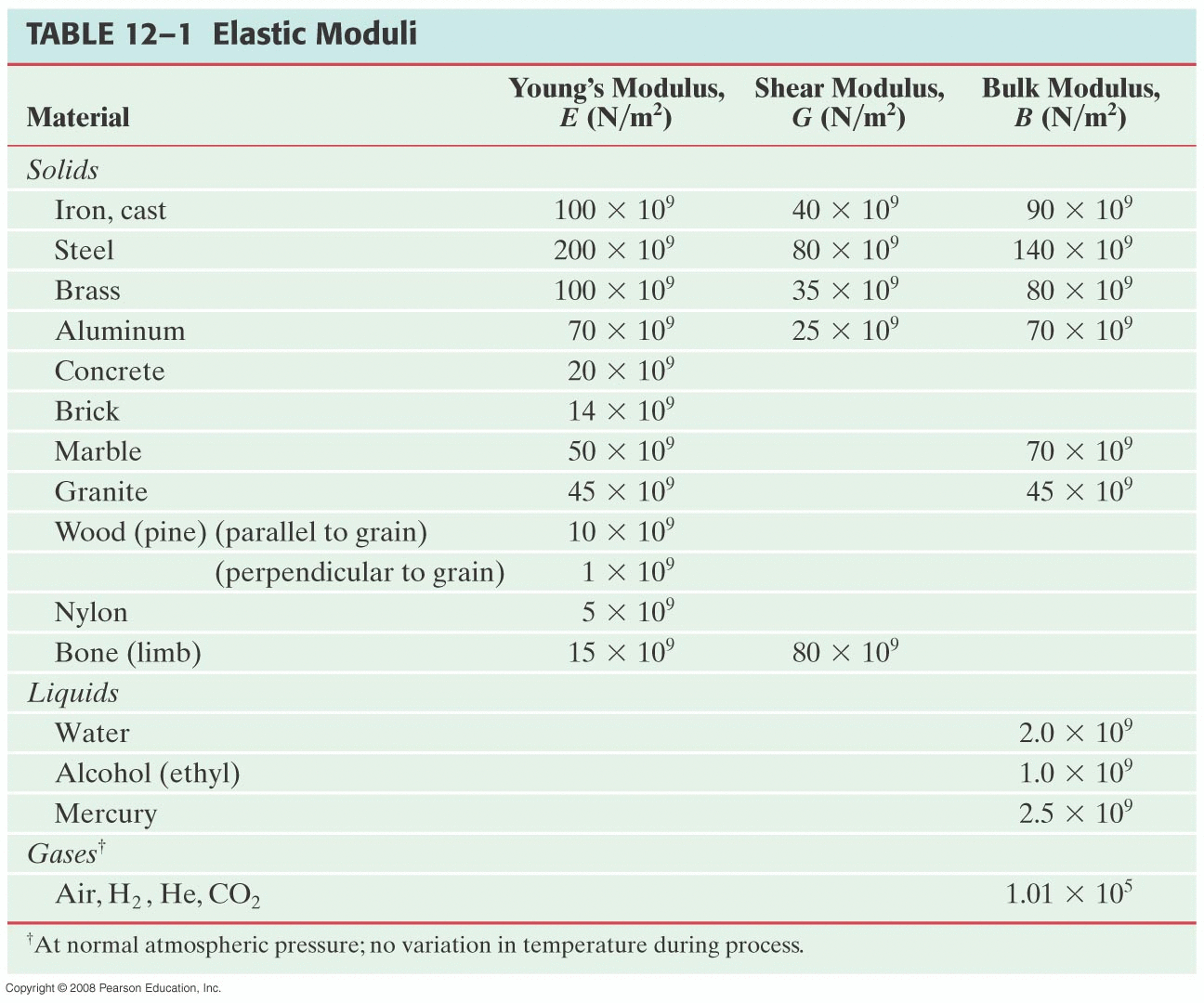
Bulk Modulus (B) If an object is subjected to inward forces from all sides, its volume will decrease: \[ \Delta V = -\frac{1}{B} V_o \Delta P \] The bulk modulus of the material (typically gas or liquid) then is: \[ B = - \frac{ \Delta P}{ \Delta V / V_o } \] (Since the volume decreases as the pressure increases, that negative sign is thrown in to make the B values themselves positive.) (See table 12-1 below for some selected values.)
The derivation will show that: Wave speed for longitudinal (P) waves in liquids and gasses: \[ v = \sqrt{B/\rho} \] where:   ρ is the density of the medium   B is the bulk modulus of the medium
"No variation in temperature" → isothermal → NOT our situation
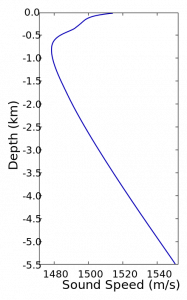
Speed of Sound in Air At STP: B = 1.42 X 105 N/m2 ρ = 1.293 kg/m3 Estimate vsound   Actual Results:	Speed of Sound in Water At STP: B = 2 X 109 N/m2 ρ = 997 kg/m3 Estimate vsound   Actual Results:

 

Transverse (S) Waves on a String/Wire
\[ v = \sqrt{ F_T / \mu } \] where:   FT is the tension in the wire   μ is the mass per length (M/L) of the medium
Example : A 20 kg bucket of rocks is hanging at the end of an 80 m long rope that has a mass of 2 kg. If we wiggle the rope, how fast will the disturbance propagate (a) at the bottom of the rope, and (b) at the top of the rope?
Example : A steel (ρ = 7800 kg/m3) guitar string is under 46.5 N of tension. If the string is 60 cm long with a diameter of 0.22 mm, what will the wave speed be on this wire? We'll see later how this translates into the frequency (330 Hz) the string will emit when played. (This is the 'high E' string on a guitar.)

 

Longitudinal (P) Waves (in solids)
\[ v = \sqrt{E/\rho} \] where:   ρ is the density of the medium   E is the elastic modulus of the material. (Also called the Young's modulus or the modulus of elasticity.) If we take a solid with some cross sectional area A and apply a force F as shown in the figure, it's length will change by: \[ \Delta l = \frac{1}{E} l_o \frac{F}{A} \]
Shear (S) Waves (in solids)
\[ v = \sqrt{G/\rho} \] where:   ρ is the density of the medium   G is the shear modulus of the material. (Also called the modulus of rigidity.) Here the material is not under tension along it's length, so it's not like the wire under tension previously. Here a force is applied laterally, causing the object to deform laterally by some Δl. In this case: \[ \Delta l = \frac{1}{G} l_o \frac{F}{A} \]
Example: Speed of Sound in Metal   A train rolling along steel tracks can excite both longitudinal (P) and transverse (S) wave types. Determine these two wave speeds.  Steel density : ρ ≈ 7800 kg/m3  Young's modulus : E ≈ 200 X 109 N/m2  Shear modulus : G ≈ 80 X 109 N/m2   Longitudinal : 5060 m/s Transverse (shear) : 3200 m/s

 

Surface Waves
Whenever two materials of different density are in contact (like the air-water interface at the surface of a body of water), waves can propagate along that interface. These are generally called 'surface waves', 'density waves' or 'gravity waves' (not related to the ripples in space/time which are also called gravity waves).
The equation for the wave speed is quite complicated in the general case, but simplifies in two useful limiting scenarios for air-water interface waves: 'shallow water limit' (when the wavelength is much LONGER than the water depth) 'deep water limit' (when the wavelength is much SHORTER than the water depth)
If the wavelength (λ) is much larger than the water depth (d) (the so-called shallow water limit), then: \[ v \approx \sqrt{gd} \] If the wavelength (λ) is much shorter than the water depth (d) (the so-called deep water limit), then: \[ v \approx \sqrt{g/k} \] where k is the wave number, defined as: \[ k = 2 \pi / \lambda \]
Example: Tsunami Wave
Early on, we talked about a tsunami with a wavelength of λ = 800 km and period of T=3600 sec. Let's use that information to ESTIMATE the (average) water depth where these values were measured. As a check: The average water depth in the Pacific ocean is about 4300 meters (4.3 km), and the maximum depth is a little over 11,000 meters (11 km). The 800 km wavelength is far larger than the water depth, so technically a tsunami (in deep water) is a shallow water wave(!). Estimate the water depth using the wave speed we found earlier for these waves (v=λ/T=222 m/s).

 

15.3 : Energy Transported by Waves
Suppose we have a transverse wave travelling along a linear medium like a string or wire.
If we focus on a tiny calculus-sized infinitesimal piece of the material that has a mass m, it will oscillate with some amplitude A as the wave passes through that point. This little mass element is undergoing simple harmonic motion, so there's some effective spring constant involved, and we found that the total energy related to the motion of this mass is E = ½kA2 (with that energy sloshing between kinetic and potential energies). Recall: \( \omega = \sqrt{k/m} \)   so   k = m ω2 with ω = 2 π f so we can write this as k = (m)( 2 π f)2. The energy involved in this little fragment of the material then is: E = ½kA2 = ½ ( 4 π2 f2 m ) A2 or: E = 2 π2 m f2 A2
We will show that the power (energy per time) carried by the wave is: \[ P = \frac{ \Delta E }{ \Delta t} = 2 \pi^2 f^2 A^2 \mu v \]
Example: Power required to wiggle a rope
A 20 kg bucket of rocks is hanging at the end of an 80 m long rope that has a mass of 2 kg. At the bottom, we wiggle the rope with an amplitude of A=5 cm at a frequency of f=2 Hz. How much power does this require? We found earlier that the tension in the rope changes (increases) as we move from the bottom to the top of the rope. Assuming there aren't any energy losses involved here, what is different about the wave when it reaches the top of the rope?