16.1 : Characteristics of Sound

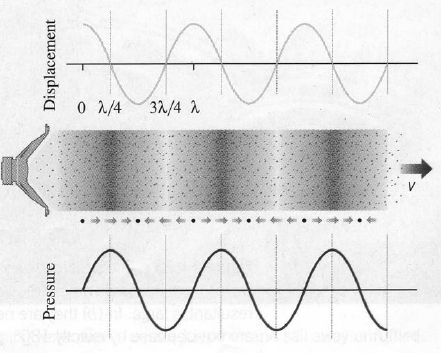
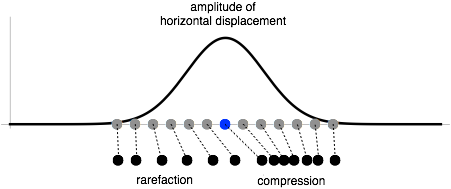
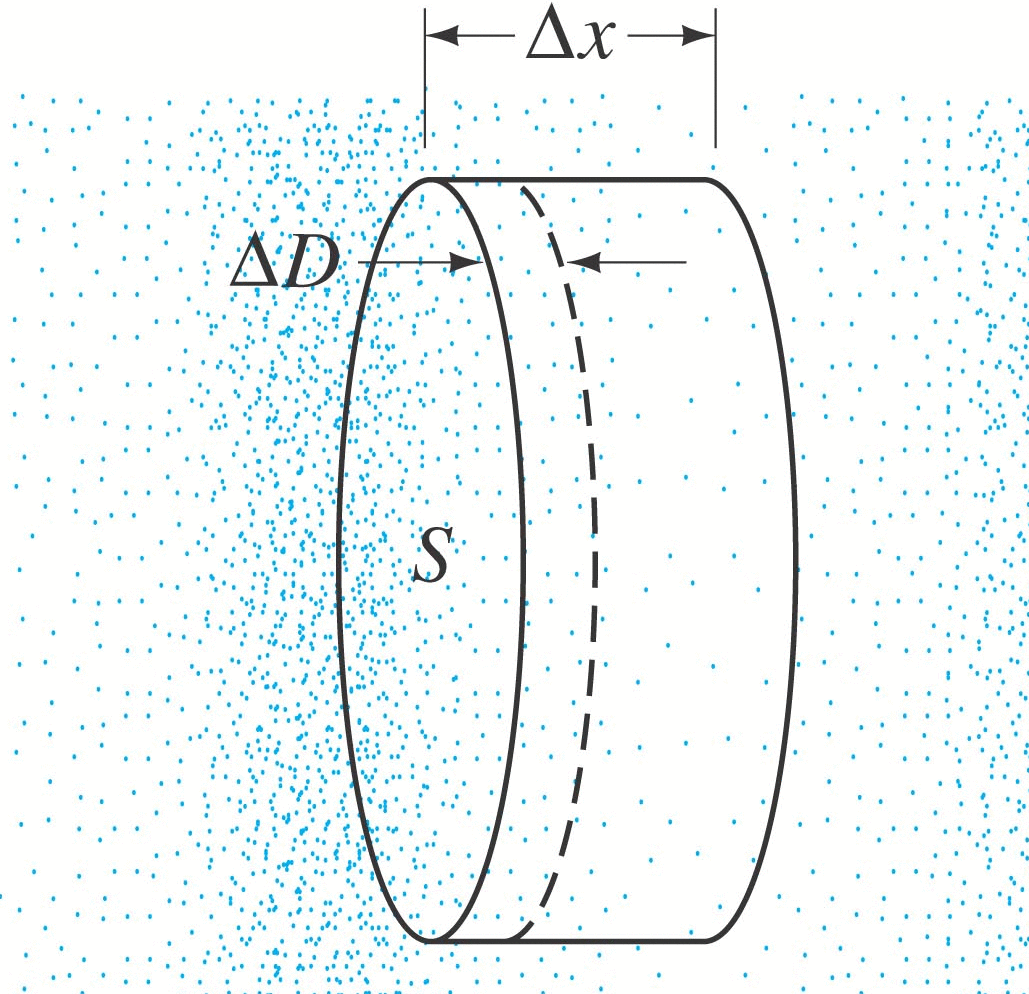
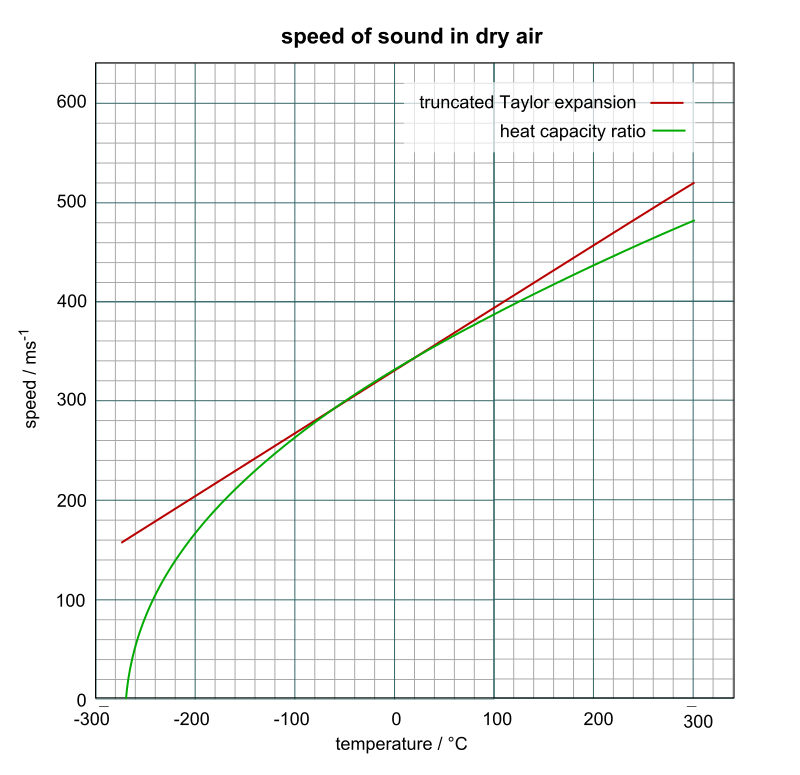
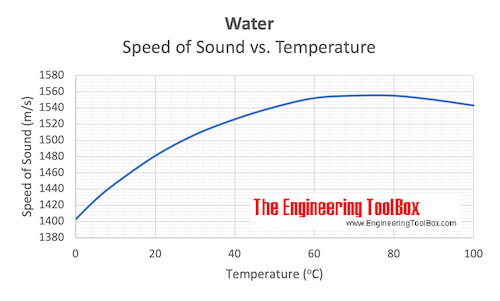
• Sound is a longitudinal (P) wave, commonly propagating through air (any gas really) or water (or any liquid). Pretty much any P-waves can be considered `sound' waves though.  • Speed of sound : from the previous chapter (for gasses and liquids) \[ v = \sqrt{ B/\rho} \] where B is the bulk modulus of the medium and ρ the volume density.  • In gasses and liquids, the density can change with temperature (especially with gasses), so the speed of sound will vary. (thermodynamics: PV=nRT). Approximate speed of sound in air (for `human' range of temperatures anyway): \[ v \approx ( 331 + 0.60T )~m/s \] where T is the temperature in deg C.  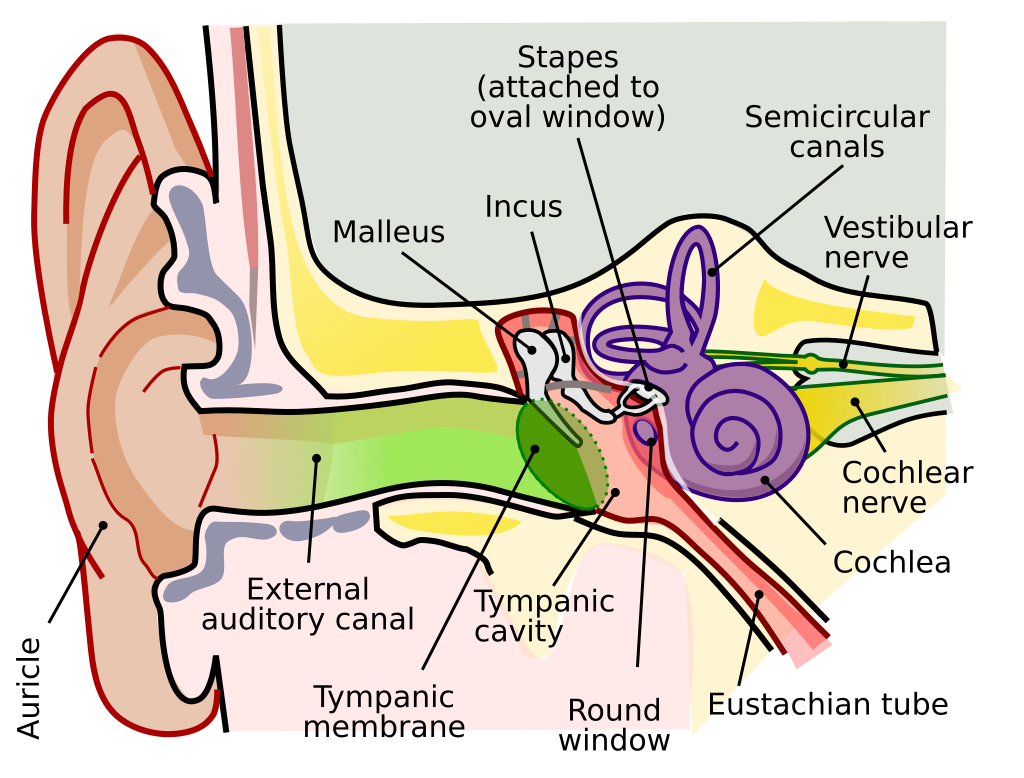• Loudness : related to the intensity of the waves (twice the intensity 'sounds like' twice as loud (about), but our hearing is not very linear)  • Pitch : another name for the frequency  • Range of human hearing : roughly 20 to 20,000 Hz.  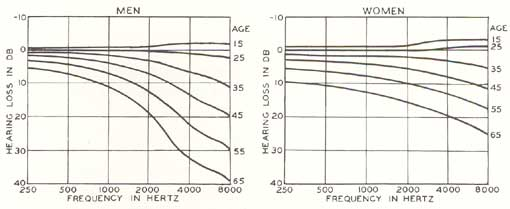• Ultrasound : f above 20,000 Hz  • Infrasound : f below 20 Hz (can have health effects) Audio Range and Sensitivity Decrease with Age

 

Speed of Sound in Air
If we look at dry air at standard pressure (1 atmosphere), the speed of sound can vary significantly with temperature. On Earth: the lowest recorded temperature was T = -89.2o C (about -128o F) in 2011 in Antarctica. the highest recorded temperature was +56.67o C (about 134o F) in 1913 in California in the aptly named `Furnace Creek' area. Over that fairly large range, the speed of sound in air is well fit by a simple linear relationship that is 'good enough' for anything we'll be doing: \[ v \approx ( 331 + 0.60T )~m/s \] where T is the temperature in deg C.
Example : The flash from a lightning strike travels at the speed of light; the sound from the thunder travels at the speed of sound. If we are exactly one mile away from the strike, how many seconds later will we hear the sound?

Temperature	Sound Speed	Time
-89.2o C (lowest recorded)	277.5 m/s	5.8 sec
+20.0o C ("normal")	343.0 m/s	4.7 sec
+56.7o C (highest recorded)	365.0 m/s	4.4 sec

 

Speed of Sound in Water
Unlike the situation above, the speed of sound in water varies much more with temperature than the speed of sound in air over the range of temperatures encountered. This variation is something that sonar systems need to account for. (These changes can greatly affect how sonar waves propagate; part of the cat-and-mouse 'game' submarines play with surface ships.)

 

16.2 : Mathematical Representation of Longitudinal Waves
We've been using the form D = A sin(kx-ωt) which describes the displacement of molecules in the medium as the wave passes by. That's interesting but not an easy quantity to measure, so pressure is used more often.   Sound is a longitudinal wave, meaning the displacement is in the same direction as the wave is travelling. The molecules in the medium (whether gas or liquid) get alternately compressed and rarified as the wave passes through a given location.   Suppose we have a continuous sine wave displacement wave function and see what effect it's having on the molecules. We'll arbitrarily pick some time and call it t=0 so the longitudinal displacement of the molecules will be D(x) = A sin(kx) as shown below.
Snapshot of sinusoidal displacement wave function	Snapshot of Gaussian displacement wave function
Note that in these snapshots, the molecules have moved to create regions of higher vs lower pressure.

 

Relating Displacement to Pressure Directly
Here we'll develop the mathematical relationship between the displacement wave function D(x,t) and the corresponding pressure wave function ΔP(x,t): \[ \Delta P = -B \frac{ \partial D }{ \partial x } \] If the molecular displacement wave function is: \[ D(x,t) = A\sin{(kx-\omega t)} \] then the pressure change (from ambient) would be: \[ \Delta P(x,t) = -BAk\cos{(kx-\omega t)} \] The amplitude of the pressure fluctuations then is: ΔPmax=BAk
These figures show the molecular displacement and corresponding pressure change at some snapshot in time for a pure sine wave 'sound'.   TOP : Molecular displacement         BOTTOM : corresponding pressure change
Some Useful Relationships
Recall v=λ/T=ω/k   so   k=ω/v   or just:   k=2πf/v Also:   v=SQRT(B/ρ)   so   B=ρv2   and we can write:    ΔPmax = BAk = ρv2Ak = 2πρvAf (relating pressure directly to amplitude and quantities we probably have easier access to)   So far, all this is still connected to individual molecular displacement amplitudes (which is interesting but not easy to measure), so let's see if we can eliminate 'A'.   Earlier, we related intensity (power/area) directly to displacement amplitude: I = 2 π2ρvA2f2 Combining that with what we just found, a useful connection is found:   \[ I = \frac{ ( \Delta P_{max} )^2 }{ 2 v \rho } \] directly connecting the intensity of the wave to the pressure fluctuations.
Speaker Example again
Earlier we looked at a 40 W speaker putting out a pure tone of f=1000 Hz. Assume the sound is spreading uniformly in all directions (unlikely with real speakers), and that we're interested on a point that is 2 m away from the speaker. At this location:  • Determine the amplitude of the pressure fluctuations as the sound passes through the air.  • Determine the displacement amplitude of the molecules in the air.  • What force will this sound exert on your eardrum?
Average adult eardrum is a roughly circular disk about 10 mm in diameter. STP: 1 atmosphere (ATM) of pressure here at the surface is about 14.7 lb/in2 or 101,325 N/m2 Common pressure units: 1 N/m2 = 1 Pa (Pascal) This speaker is putting out a painfully loud sound. What pressure fluctuations does it represent in terms of ATM units? (The ear is incredibly sensitive!)

 

16.4 : Sources of Sound
Vibrating Wires/Strings : quick review   We saw last time that two identical waves travelling in opposite directions can create standing waves and one scenario where these appear is in vibrating strings or wires, which appear in stringed musical instruments. These standing wave patterns imply that the length of the string is some integer multiple of the wavelength of the waves: \[ L = N ( \frac{ \lambda }{2} ) \] which means that only select wavelengths will 'fit' on the wire - wavelengths such that: \[ \lambda_N = \frac{2L}{N} \] and since v=λ/T=λf, this implies the wire will vibrate with frequencies of: \[ f_N = N ( \frac{v}{2L} ) \] where: \[ v = \sqrt{F_T / \mu } \] These frequencies are all integer multiples of the wire's lowest frequency, called the fundamental.
Example : An Old Test Problem   The spokes in a bicycle wheel need to be adjusted to the proper tension. One way bike shops do this is to bang on each spoke and check what frequency of sound it emits. If the note is too low or high, they'll adjust the tension accordingly. Suppose we have a spoke that is 26.2 cm long and made of a solid 15-gauge stainless steel wire (which means it has a diameter of 1.8 mm and a density of 8000 kg/m3. What spoke tension is needed so that, when vibrating at its fundamental frequency, it produces sound with a frequency of 440 Hz? FT = v2μ = v2M/L f1 = v/(2L) so v=2Lf1 = 230.56 m/s M=(density)*(volume) = (density)*(area)*(length) so: M = (ρ)( π d2/4)(L) = 5.336 X 10-3 kg (Actual value range: 980 to 1200 N)

 

Vibrating Air Columns

The same standing-wave phenomenon can happen with pressure waves, but figuring out what patterns of waves have to `fit' in a given length is slightly more tricky. Open Pipe : Consider a hollow tube, open at both ends as shown in the figure below. The air molecules at each end can move left or right in the figure - there's nothing stopping them from doing so. The important figure is on the right though where we look at what patterns of pressure fluctuations are 'allowed'.

We need a pressure node at each end of the pipe, implying: We need L = N (λ/2) with N=1,2,3,..., which in turn implies: \[ f_N = N (\frac{v}{2L}) \hspace{1em} for~~N=1,2,3,... (open~pipe) \] (same relationship we had with the vibrating strings of a stringed instrument)

 

Example : Organ Pipe

I'm simplifying the situation a bit here, but presume that an organ pipe is basically just a long hollow cylinder, open at both ends.   (a) How long would the organ pipe need to be to resonate at middle C (a frequency of f=261.626 Hz) at STP (i.e a temperature of 20o C)? \[ v \approx ( 331 + 0.60T )~m/s \] \[ f_1 = \frac{v}{2L} \]   (b) Suppose instead that it's 38o C (about 100o F) in the room. What frequency will the pipe produce? Would this be noticeable? (Yes).   (c) How can instruments in an orchestra adapt to changes in temperature?

 

Length-Adjustment Components in Wind Instruments
	Pipe organ adjustment??? (Couldn't find a reference...) Might be it sets the standard and everyone else tunes to match?