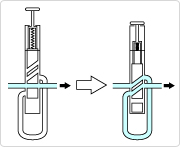
Closed Pipe
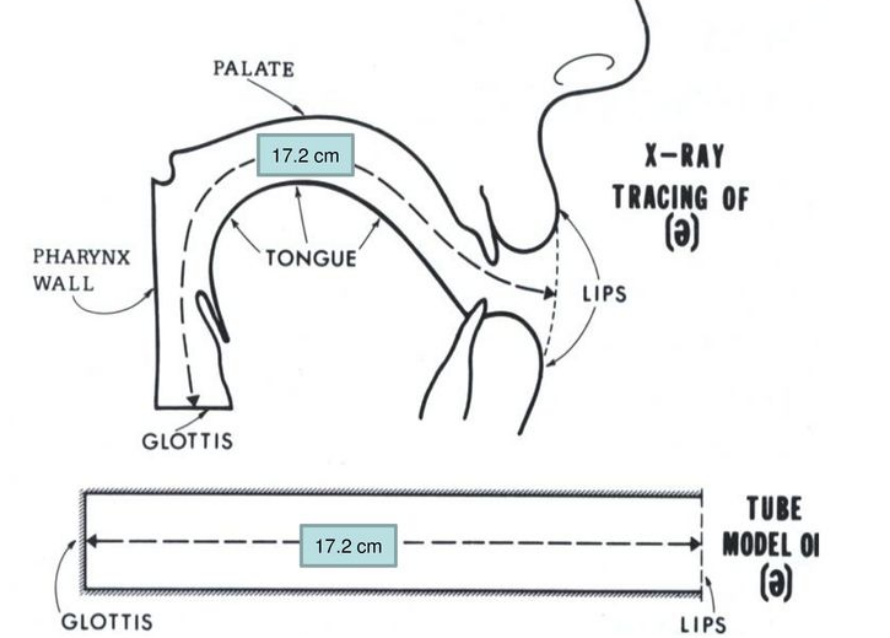
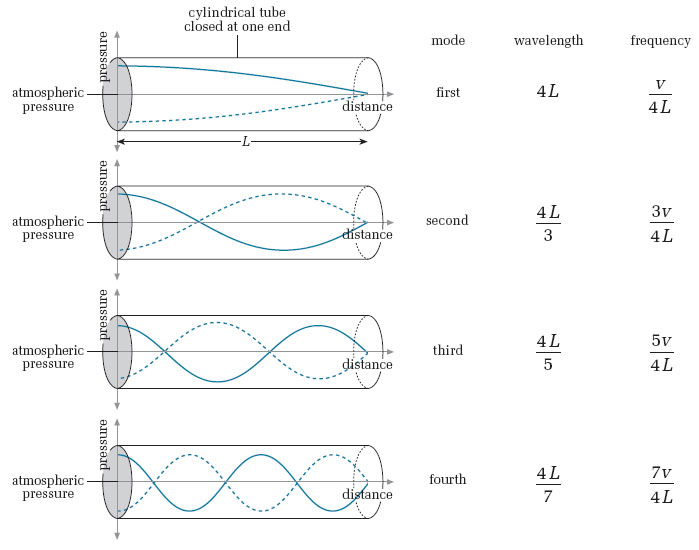
What happens if we block off one (just one!) end of the pipe? In the figure below, we block off the right end of the pipe but leave the left end open. What standing waves can exist in this geometry? • We'll need a displacement node at the solid (closed) end • We'll need a pressure node at the open end
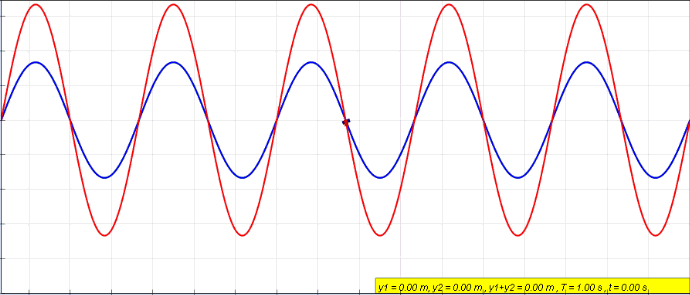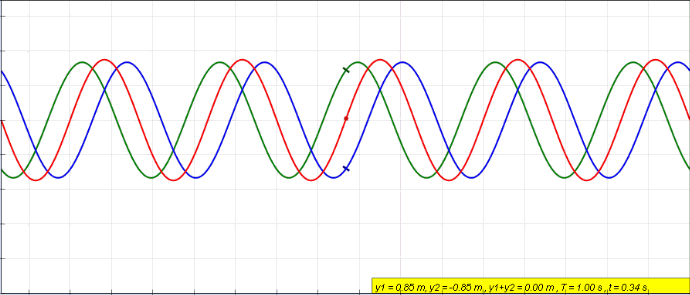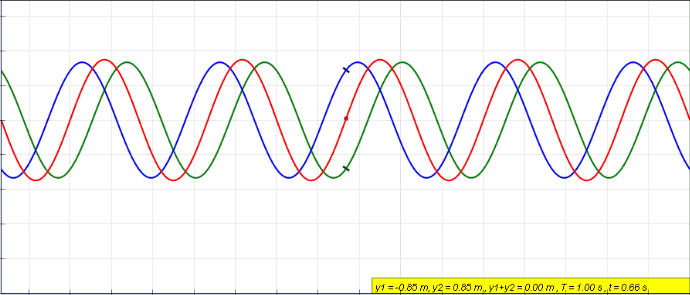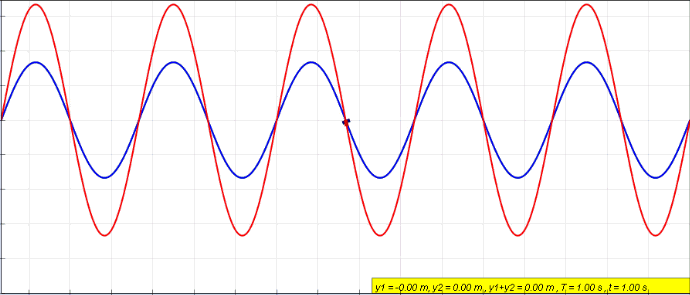
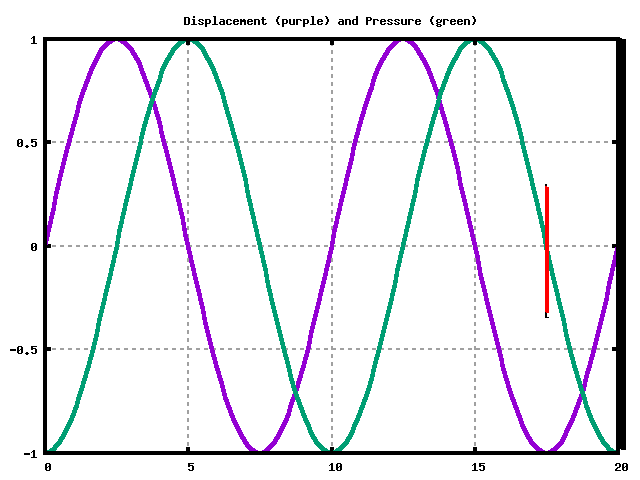
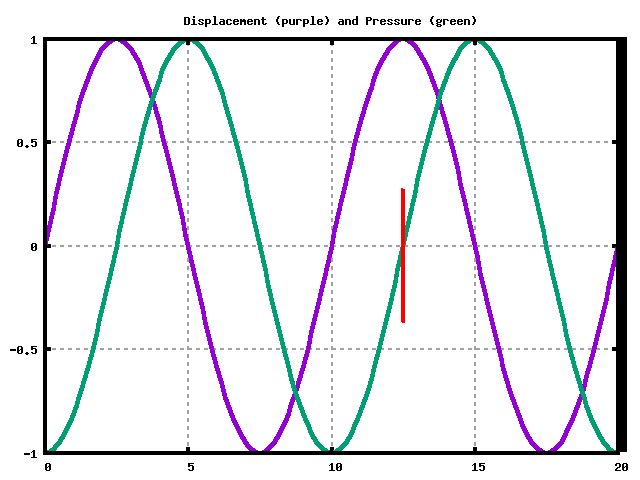
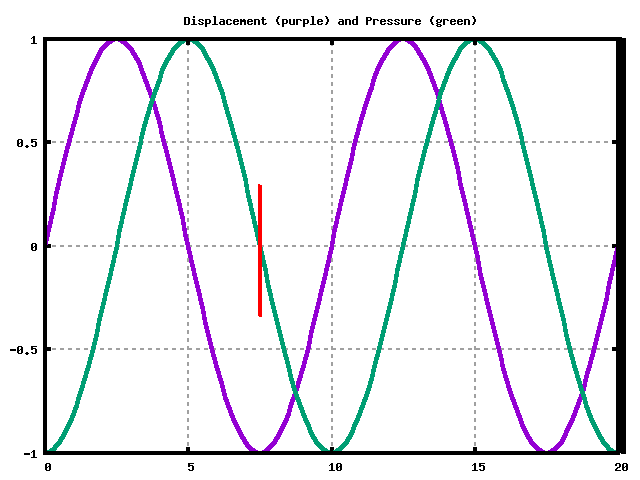
Standing Wave Animation	Snapshot of Displacement and Pressure
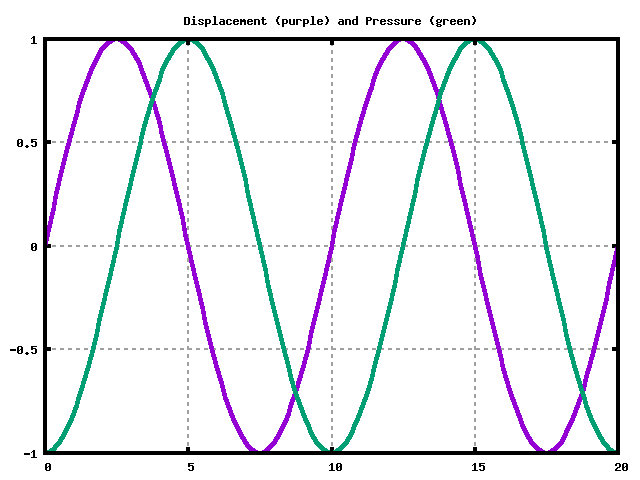
We need a displacment node (purple) at the solid end (on the right). We need a pressure node (green) at the open end (on the left).   Here are the first three situations where that would occur: Implies tube length is L=λ/4 or: \[ f = (1)( \frac{v}{4L} ) \] Implies tube length is L=3*λ/4 or: \[ f = (3)( \frac{v}{4L} ) \] Implies tube length is L=5*λ/4 or: \[ f = (5)( \frac{v}{4L} ) \]
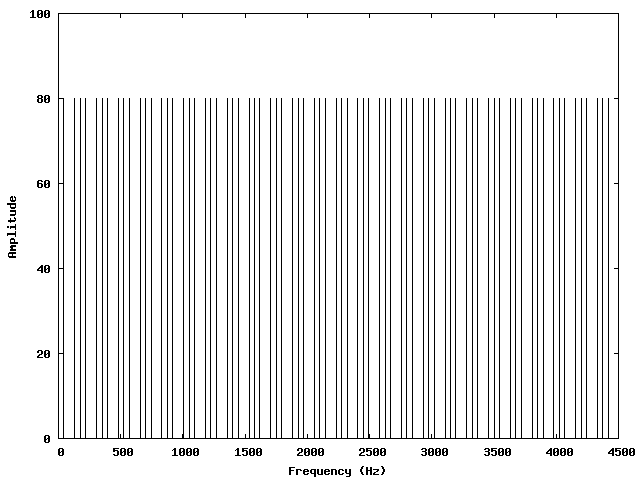
Generally, we need L = N (λ/4) with N=1,3,5,... (just odd integers this time) which implies: \[ f_N = N (\frac{v}{4L}) \hspace{1em} for~~N=1,3,5,... (closed~pipe) \] Remember: CLOSED pipe means ONE end is closed and the other is still open...

 

Example : Organ Pipe Closed at One End

How long would an organ pipe (CLOSED at one end) need to be to resonate at middle C (a frequency of f=261.626 Hz)?   If we now OPEN UP the closed end, what frequency will this pipe produce?   What opportunity does this open up?   Each doubling of frequency represents one octave. Logarithmic scale 12-step 'equally temperated chromatic scale' r is the ratio of each note to the previous, so:   r12=2 or r=2(1/12) = 1.05946309...

 

Example : Human Vocal Tract

Estimate the first three standing wave frequencies of the human vocal tract. Assume the air temperature in there is about 34o C. That creates: vsound=351.4 m/s. Standing waves would form at these frequencies, meaning there would be specific locations in the throat where the pressure anti-nodes would be, causing higher (vibrating) pressures at those points. The speed of sound in air outside the vocal tract is different (lower) than inside. What does that do to the sound?

Online tone generators:

 • OnlineToneGenerator.com

 • onlinesound.net/tone-generator

 • www.szynalski.com/tone-generator/ (can enter notes directly)

 

Double-Closed Pipe

The book doesn't consider these, noting that 'a tube closed at both ends, having no connection to the outside air, would be useless as an instrument' but that scenario still does exist. An enclosed shower stall is a good example, but any enclosed space (water tank, etc) can encounter such a situation. In this scenario, the boundary conditions would be that we need the displacement nodes to be at the boundaries of the chamber (i.e. wherever we have solid surfaces). What would be the equation for fN for a double-closed pipe?

Mixed Example : Consider a shower stall that is closed on all 4 sides (and the bottom) but open at the top. The stall is 1 meter wide, 1 meter deep, and 2 meters from the floor to the open part at the top. What (audible) standing wave frequencies will exist in this geometry?

All the audible frequencies for which standing waves will form

 

Playing an Instrument : Changing Notes
The fundamental frequency depends on the length of the pipe or string: \[ f_1 = \frac{v}{2L} \hspace{2em} (strings) \] \[ f_1 = \frac{v}{2L} \hspace{2em} (open~pipe) \] \[ f_1 = \frac{v}{4L} \hspace{2em} (closed~pipe) \] where the length L reflects the distance between appropriate nodes (displacement or pressure, depending on the situation). Basically it's all about boundary conditions.
Flute (open pipe): an opening creates the need for a pressure node at that point.	Guitar/etc : string is pushed down onto the metal frets, creating a displacement node at that point.
Where does the sound that reaches our ears come from in each case above?
Playing an Instrument : Trombone
Frequency range ('tenor trombone') : 82.4 Hz to 466.2 Hz Fundamental: f1=v/(2L) Change frequency (note) by changing length directly (pulling slide in and out):
Playing an Instrument : Trumpet
Frequency range (typical): 165 Hz to 988 Hz Length is changed using valves that introduce additional segments of 'pipe'
Frequency Range of Various Instruments

 

16.3 : Sound Intensity - decibel scale

The human ear is incredibly sensitive - it can detect intensities as low as 1 X 10-12 W/m2 and as high as 1 W/m2 at which point the sound is becoming painful (and being exposed for extended periods of time to that intensity can cause permanent damage). This is such a large dynamic range, that intensity is often converted into a logarithmic scale called the bel: \[ bel = log_{10}(I/I_o)~~where~~I_o=1 \times 10^{-12}~W/m^2 \] All the sounds we can deal with from lowest to highest then represent a range from 0 to 12 bels. That's a pretty coarse scale, so more commonly the decibel is used, where 10 decibels (dB) is 1 bel: Decibel (β) definition: \[ \beta = 10log_{10}(I/I_o)~~where~~I_o=1 \times 10^{-12}~W/m^2 \] This table gives some typical sound scenarios with the actual intensities in W/m2 and the corresponding decibel level.

 

Impact of Doubling the Intensity

Suppose we crank up the speaker from 40 W to 80 W exactly doubling the intensity. What effect does that have on the decibel level?

 

Variation with Distance

I=(power)/(area) so if we're twice as far away, what does that do to the intensity (in real terms, and in dB)?

 

Cowbells
I used to live on Nash Street (2 km from the stadium) and during a football game I could often hear the cowbells just barely. Let's call that equivalent to a 'whisper', which is an intensity of β=30 dB. (a) How much 'sound power' was being produced by the cowbells? (b) How loud (in dB) would this sound be to players on the field? (Assume they'd be roughly 50 m from the source.) (c) Why is this result not remotely correct? The actual loudness on the field will be far higher than what we'll calculate here. Why? (Attenuation of sound in air depends on lots of factors but a 'reasonable' rule of thumb is about 0.015 dB/m)

 

Air Raid / Tornado Siren
The specs for a particular air-raid siren (used more for tornado warnings) are listed as producing 138 dB of sound at a distance of 30 m from the siren. It's also claimed that this siren is powered by a 180 hp diesel motor. Let's see if the given data is consistent. Conversion: 1 HP = 746 W

 

Ear-buds Power Need
The Apple airpods pictured here allegedly can play music for 6 hours on a single battery charge. Assuming an 80 dB sound level: How much power is the speaker putting out? How much energy (in Watt-hours) is the fully charged battery storing? Typical ear-bud batteries hold about 0.05 W·h of energy. Where is the rest of this energy going?

 

Jet Engine

For a particular jet engine, a noise level of 140 dB was recorded at r=30 m from the engine.   (a) How much total sound power is the engine emitting?   (b) GTR is 30 km from MSU. How loud (theoretically) would this jet taking off sound here on campus?   Do this two ways: actual calculation using the 'distance doubling' shortcut (30 km is 1000 times 30 m, and 210=1024)   Coming back to reality, how much attenuation would 30 km of air do to this sound?

 

Air Molecule Displacement

What is the displacement amplitude of individual air molecules if a sound is at the very lowest end of human hearing? (I.e. β=0 dB.)   Assume this is a voice we can just barely hear, so the peak frequency would be around 500 to 1000 Hz. Recall:       I = 2π2ρvA2f2

 

Pain Threshold

What pressure amplitude ΔPmax does the 'pain threshold' represent?