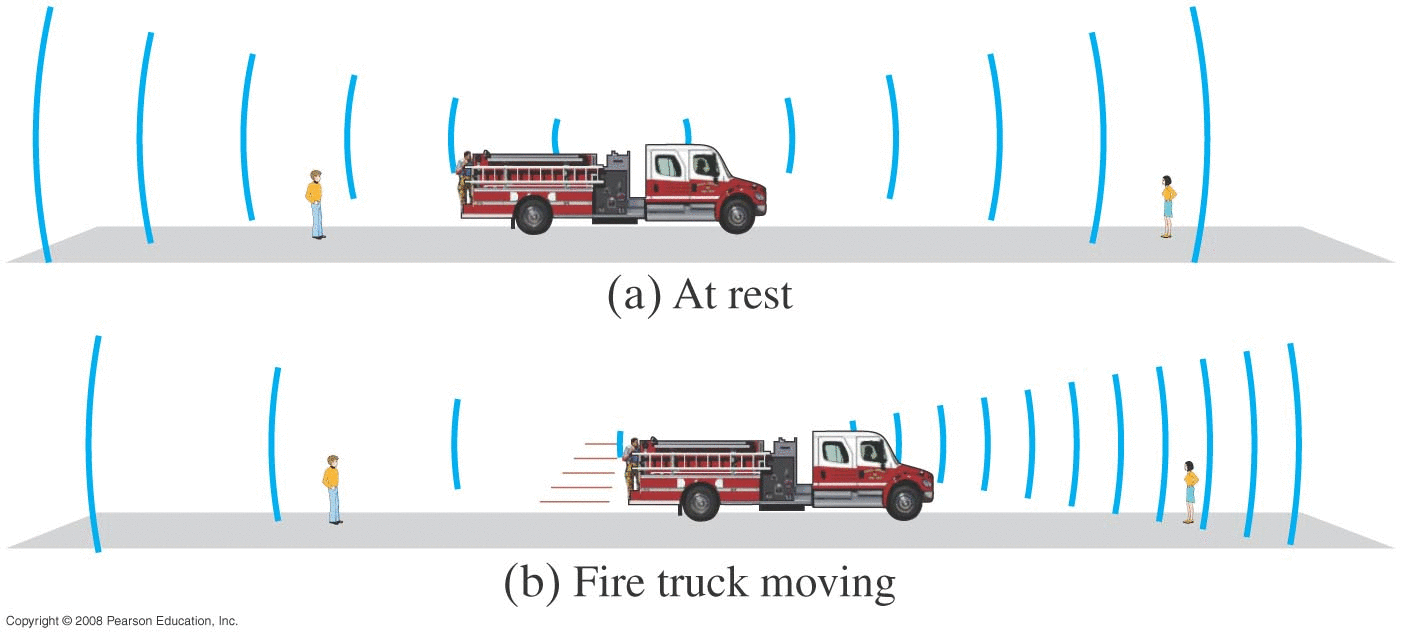
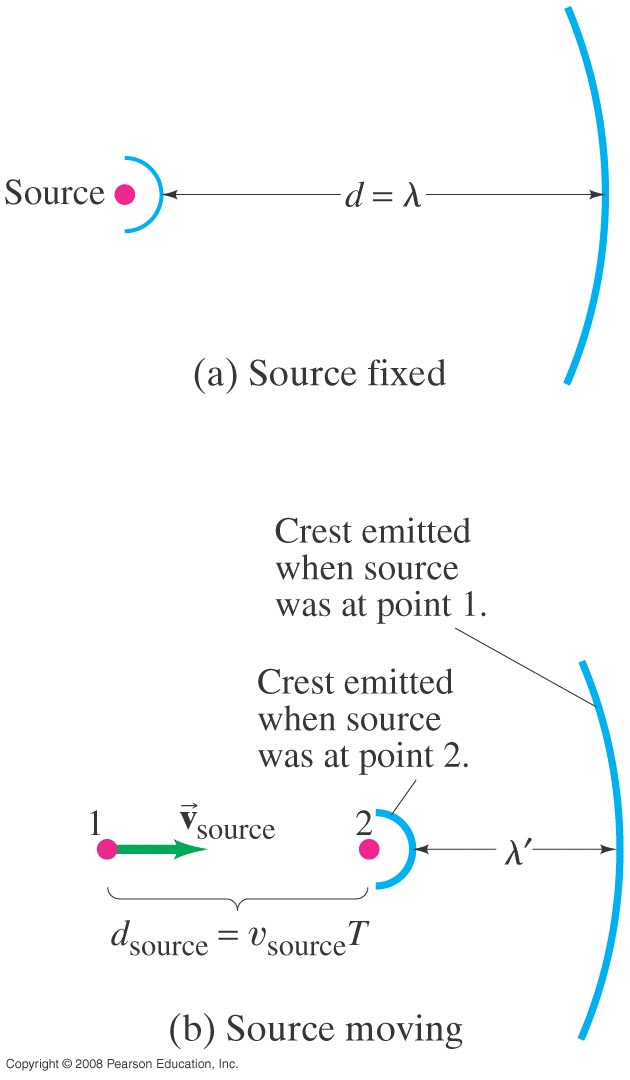
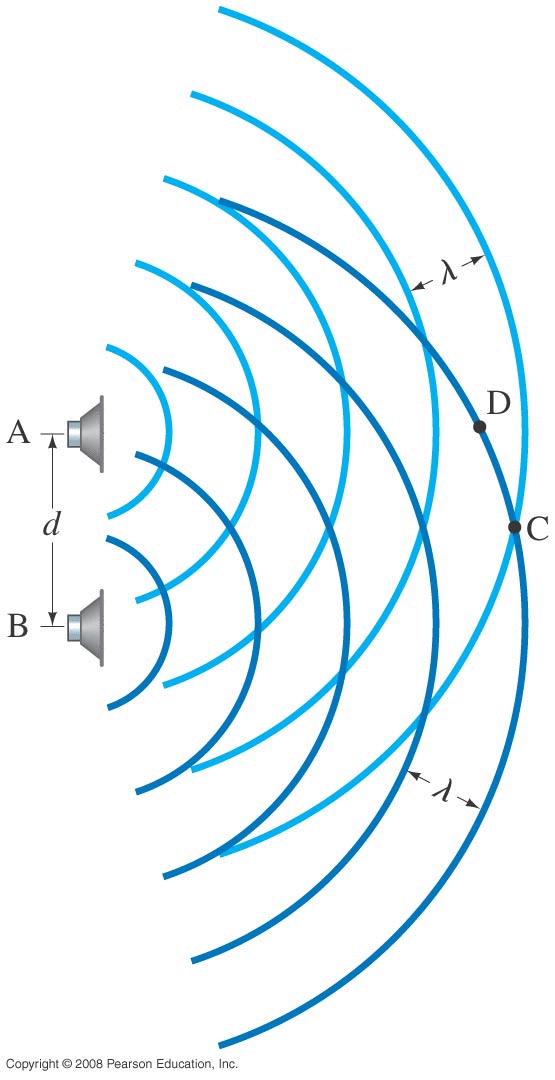
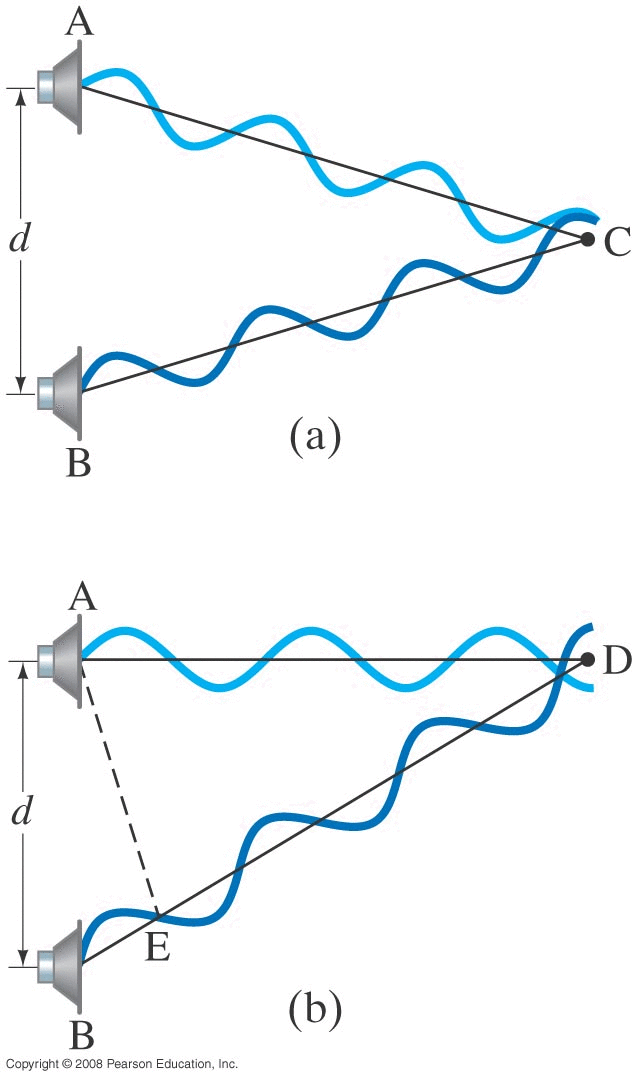
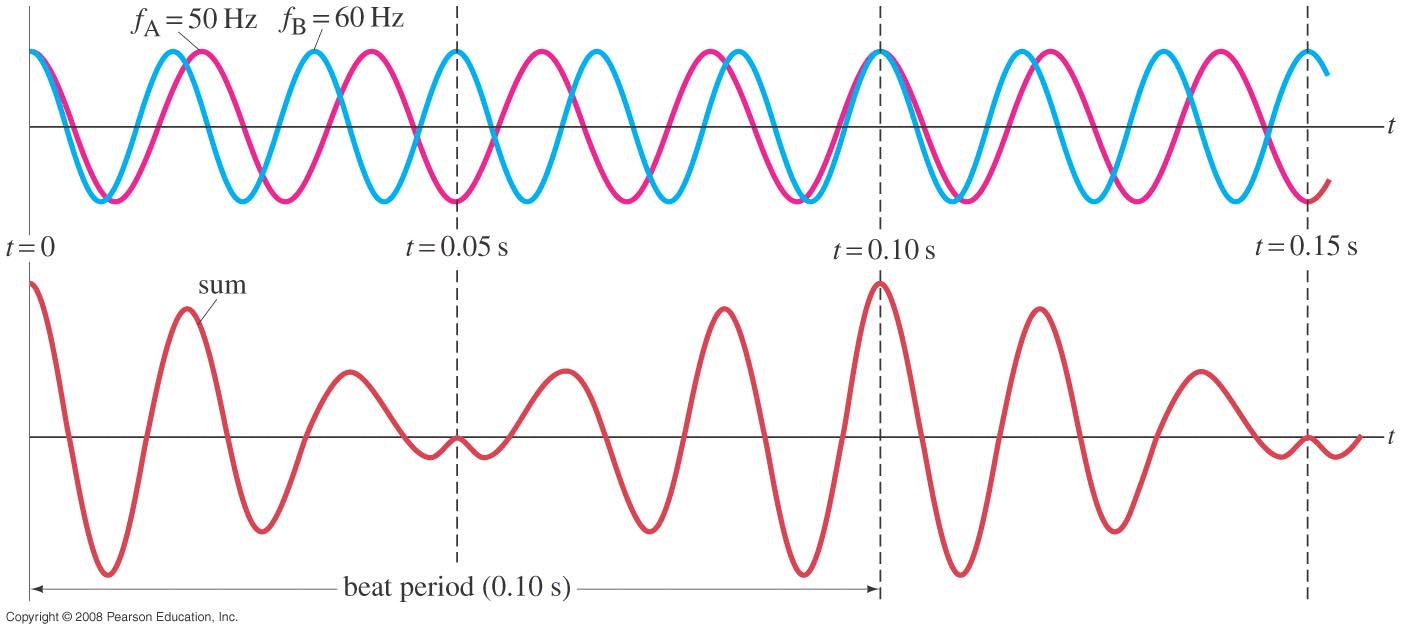
16.6 : Interference of Sound Waves (beats)

Suppose we have two sound sources that are slightly out of tune, producing frequencies that are not quite the same. What will we hear?

First source:     D1 = A cos(ω1t) Second source: D2 = A cos(ω2t) Combination:    D = D1+D2 = A cos(ω1t) + A cos(ω2t) Trig identity: \[ \cos{(X)} + \cos{ (Y) } = 2 \cos{ (\frac{X+Y}{2}) } \cos{ ( \frac{X-Y}{2} ) } \] Resulting wave function: \[ D = 2A\cos{ [ \frac{ (\omega_1 + \omega_2)t }{2} ] } \times \cos{ [ \frac{ (\omega_1 - \omega_2)t }{2} ] } \]

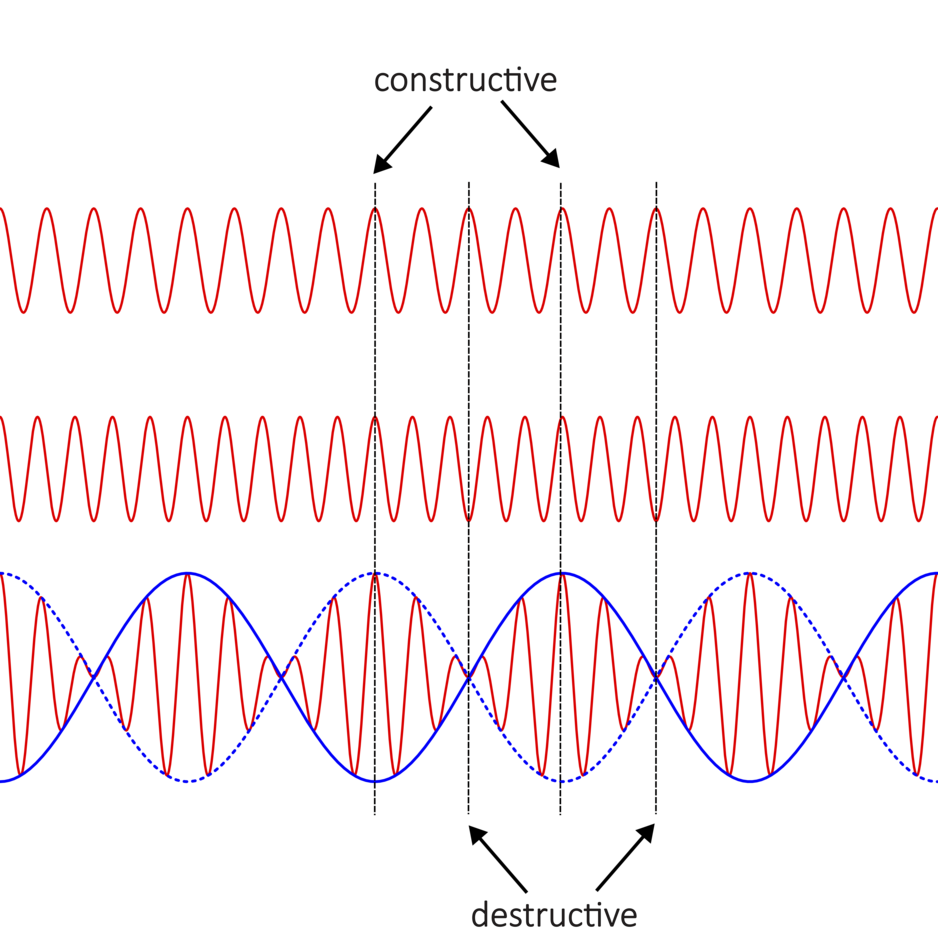
The two frequencies basically become a single frequency with \[ f_{avg} = \frac{ f_1 + f_2 }{2} \] whose amplitude is modulated at a frequency of: \[ f_{beat} = | \frac{ f_1 - f_2 }{2} | \times 2 = | f_2 - f_1 | \]   That final times 2 is because we can't hear PHASE. We hear that amplitude modulation going through highes and lows at twice the nominal beat frequency: the high amplitude points occur twice in each period of the modulating cosine.

Example: Musical Instruments Out of Tune   Suppose a violin is playing a middle C at the correct frequency of f1=261.6256 Hz but a wind instrument that's warmed up a bit is attempting to play the same note but is actually 2% higher thanks to the higher temperature so f2=266.858 Hz.   What frequency will we hear, and what 'beat frequency' will occur?   See: OnlineToneGenerator.com   There are two places where you can create two different frequencies and hear the result:  •  Binaural Beats lets you pick two frequencies and each will be played in a separate ear (so really only works correctly with headphones/earbuds).  •  Multiple Tone Generator can do 2 or more and you can turn each on and off easily. If the notes are 'close enough', our auditory system hears them as a single average frequency with a modulated amplitude. At some point though as the two frequencies get far enough apart, we start hearing them as two distinct notes.

 

16.7 : Doppler Effect

Here we'll look at what happens when either the source or the listener are moving (or both).   Example: car horn (around 45 seconds in)

Example : Suppose a firetruck is emitting sound with a frequency of f=1000 Hz and is moving at 20 m/s towards a stationary listener. What frequency will the listener hear?

Doppler Equation (this book's version)

\[ f' = f \cdot ( \frac{ v \pm v_{obs} }{ v \mp v_{src} } ) \] where:   •  f = frequency source thinks it's creating   •  f' = frequency observer actually hears   •  v = vsnd : the speed of sound in the medium   •  vobs = observer speed (always positive)   •  vsrc = source speed (always positive)   •  Upper sign if that entity (src or obs) is moving towards the other   •  Lower sign if that entity (src or obs) is moving away from the other   •  Separate analysis for each term to determine signs

Example : Suppose the firetruck is emitting sound with a frequency of f=1000 Hz and is moving at 20 m/s away from a stationary listener. What frequency will the listener hear?

Example : Suppose the firetruck is emitting sound with a frequency of f=1000 Hz and is moving at 20 m/s to the right, and the listener is in a car that's ahead of the firetruck and travelling at 10 m/s, also to the right. What frequency will the listener hear?

Example : Double-Doppler Scenario   Suppose the firetruck is emitting sound with a frequency of f=1000 Hz and is moving at 20 m/s to the right. Directly ahead of the truck is a stationary flat wall that will reflect sound back towards the truck. What frequency will someone in the firetruck hear? They'll also hear the sound travelling directly from the siren to their ears. What frequency will that be? Will they hear 'beats' between these two?   OnlineToneGenerator.com

 

Constructive and Destructive Interference
Suppose we have two sources putting out the same frequency f that are separated by some distance. If we stand at some other location, what will we hear?
Point C : exactly 5 wavelengths from each speaker (like upper right figure) Point D : exactly 5 wavelengths from speaker B, but just 4.5 wavelengths from speaker A (like lower right figure)
Suppose we're in a room where the speakers are mounted on the wall d=2 m apart from one another. If we sit somewhere equidistant from each speaker (i.e. along the midline coming out perpendicular to the wall), then the distance from us to each speaker is the same and whatever f is, the waves from those two sources always arrive `in phase' with one another and we hear a nice loud sound. What if we move a bit off to one side? Suppose we're 4 m away from the wall, and directly in front of speaker A. (Basically the lower right figure above.) At what frequencies will constructive interference occur? (I.e. for what frequencies will the distance difference be exactly an integer number of wavelengths? At what frequencies will destructive interference occur? (I.e. for what frequencies will the distance difference be exactly an integer number of wavelengths plus an additional half-wavelength? (Assume vsnd=343 m/s in this room.) (Real-world reality check: why don't we notice these 'missing' frequencies? What other paths does the sound take from the speaker to our ears?)

 

Far-Field Approximation

Suppose we are 'very far away' from the two sources. In this geometry, the paths from each speaker to where we're located are nearly parallel which gives us a 'short cut' to finding the path difference: Path Difference = Δ s = d sin(θ) Constructive Interference: \[ d \sin{\theta} = m \lambda \hspace{3em} for~~m=0,1,2,\cdots \] Destructive Interference: \[ d \sin{\theta} = (m+\frac{1}{2}) \lambda \hspace{3em} for~~m=0,1,2,\cdots \]   Suppose the two speakers are emitting the identical middle C note so f=262 Hz. (Assume vsnd=343 m/s.) At what angles will constructive and destructive interference occur if we are very far away from these speakers?