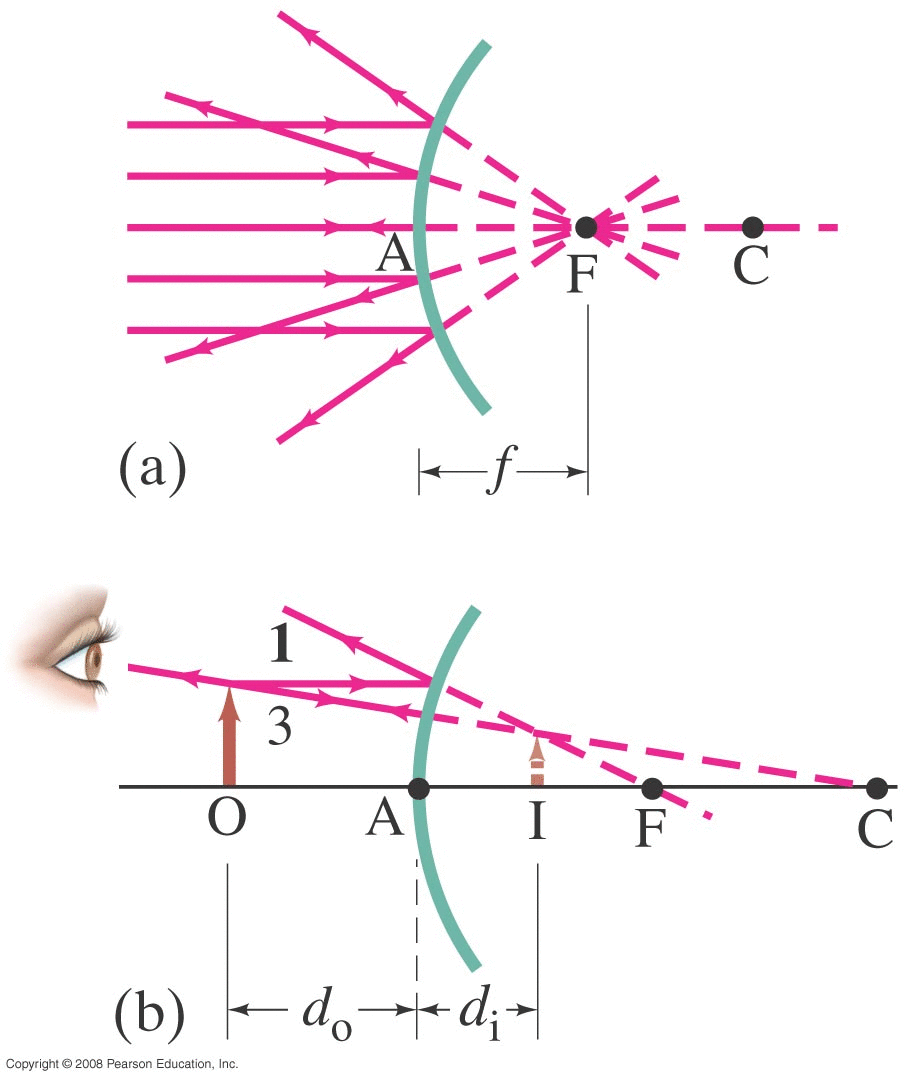Chapter 32 : Light Reflection and Refraction

Review

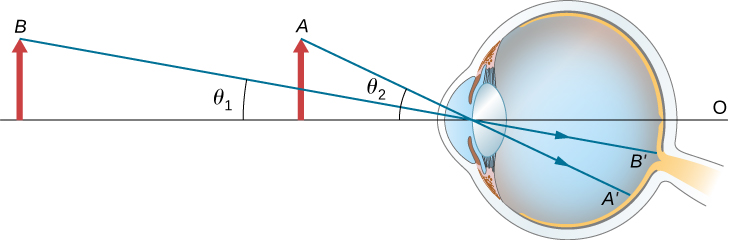
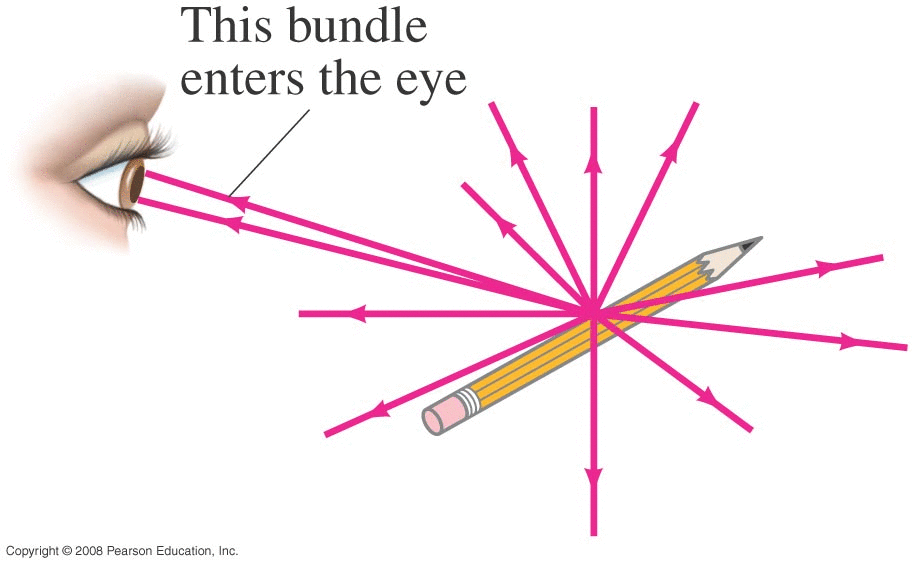
How we 'see' an object: light falls on the object; 'photons' are scattered in 'all' directions, travelling in straight lines at the speed of light. Some make it through our pupil and land on our retina.

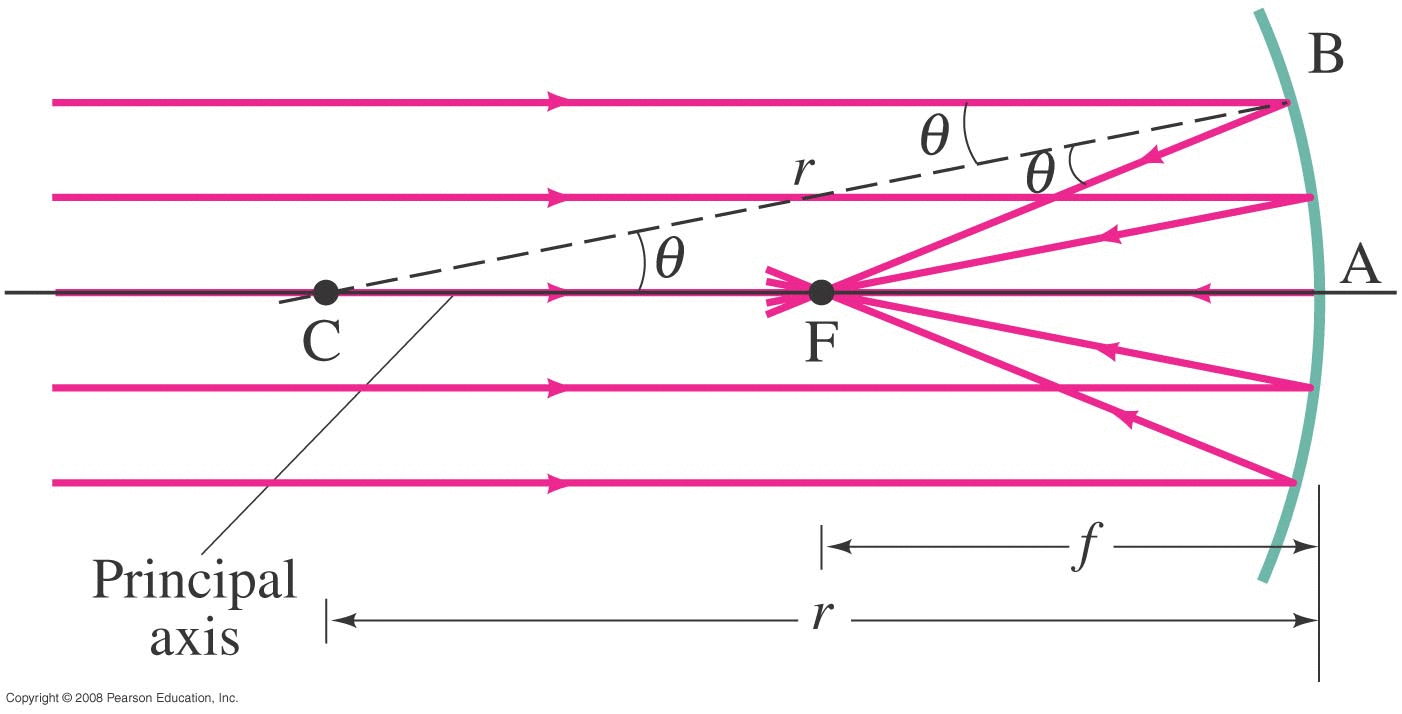
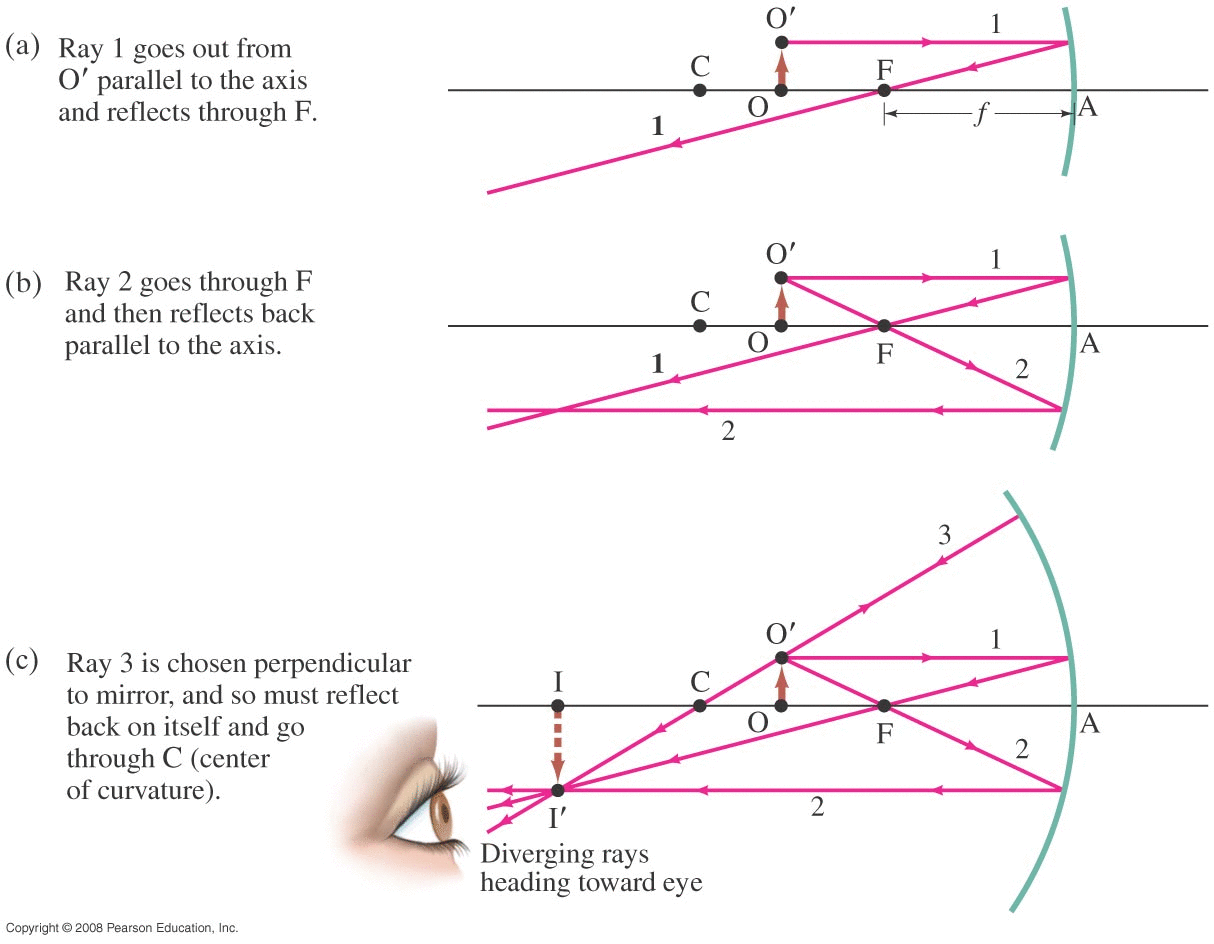
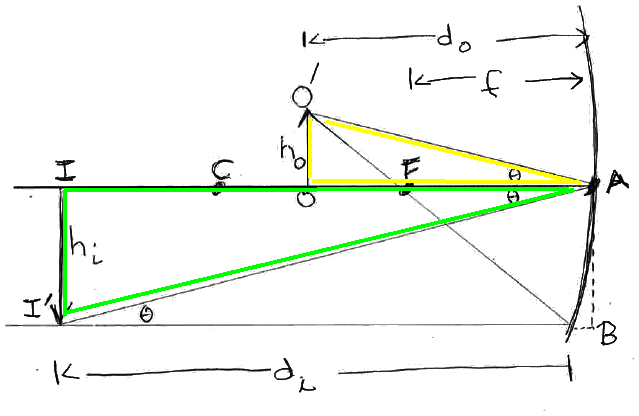
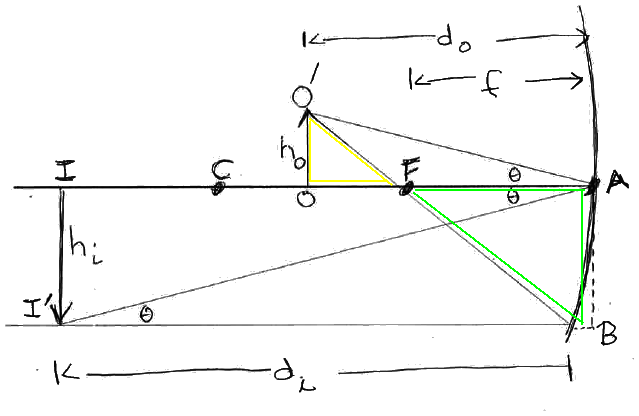
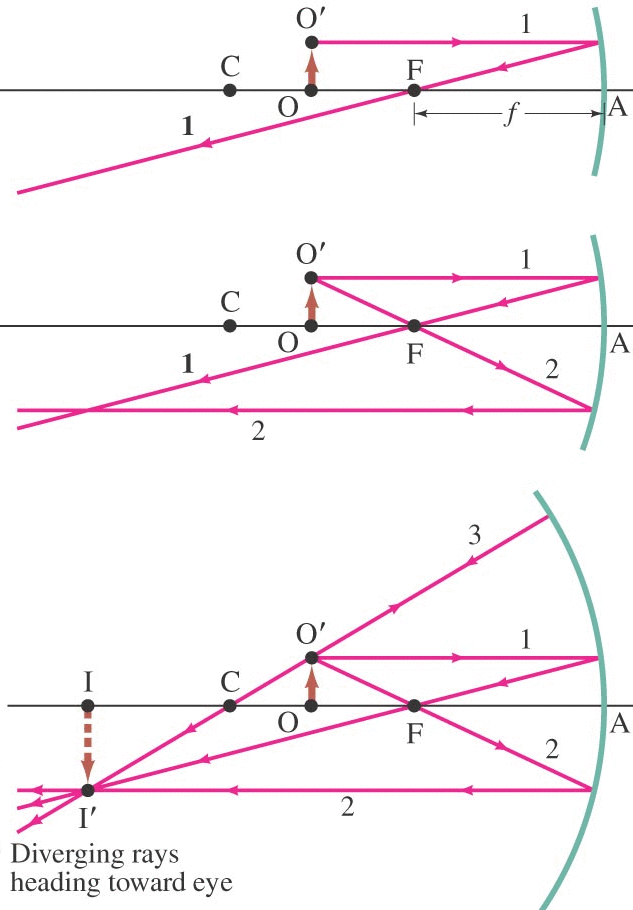
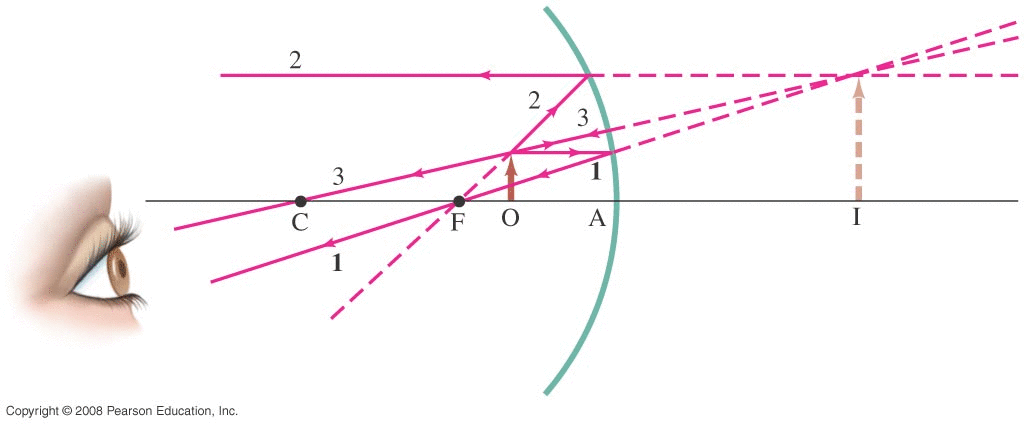
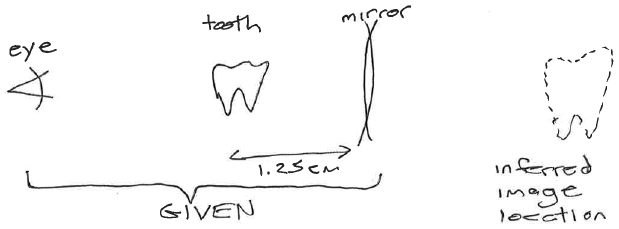
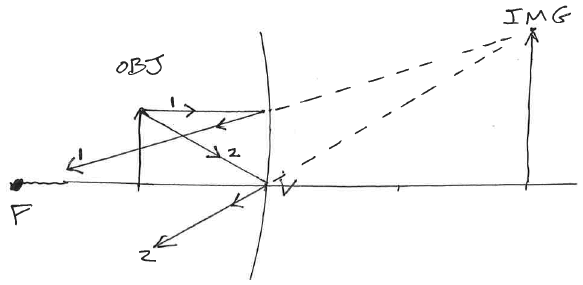
Concave Mirror (piece of a spherical surface of radius R, centered at C): photons (light rays) coming in from 'far away' are nearly parallel. θ_r=θ_i when each ray reflects. We found that (to first order) all these rays converge at a single point F (the 'focal point' of the mirror) with f=R/2.

Ray Diagrams for Spherical Mirrors

Place an object between C and F in front of a concave mirror (illustrated as an arrow from O to O').
Photons will be flying off from the top of the object in all directions. Let's follow a few of them and see what path each takes:

According to our eye, these photons appear to be coming from point I'. We 'see' an upside down version of the object (the 'image') as if it were actually located at that point.

Principal Rays

Photons from a point are flying out at 'all' angles, and all will pass through a corresponding image point I'. There are basically FOUR whose paths are easy to draw, called PRINCIPAL RAYS, producing what is called a RAY DIAGRAM.

A ray parallel to the axis reflects through F. (useful)
A ray through F reflects into a ray parallel to the axis. (useful)
A ray that's a radial (as if it came from point C) reflects right back along the same line. (rarely useful)
(Not shown above.) A ray that hits the vertex V (labelled A in the figure) reflects such that the angle below the axis is the same as the incoming ray above the axis. (useful)

Mirror Equation and Magnification

Let's use a few of these rays to convert the ray diagram into an equation that relates the object and image locations.

Using the vertex ray (O'-A'-I') the yellow and green triangles are similar triangles.
\[ \frac{h_o}{d_o} = \frac{ | h_i | }{ d_i } \]

Sign convention: if h_o is a positive number, then h_i here should be considered negative so h_i = -|h_i|, leading to:
\[ \frac{h_o}{d_o} = \frac{ - h_i }{ d_i } \]

Flip that over and rearrange a bit:
\[ \frac{h_i}{h_o} = - \frac{ d_i }{ d_o } \]

The ratio of image height to object height is called the magnification of the mirror, so:

\[ m = \frac{h_i}{h_o} = - \frac{ d_i }{ d_o } \]
MAGNIFICATION

Where will the image be located? Let's use a different ray and another pair of similar triangles:

Using the ray that passes through F (O'-F-B-I') the yellow and green triangles are similar triangles.
Comparing the ratio of the height to the base for each triangle:
\[ \frac{h_o}{d_o - f} = \frac{ - h_i }{ f } \]

Rearranging:
\[ \frac{h_i}{h_o} = - \frac{f}{ d_o - f} \]

The left side is the magnification m which we found was also equal to m=h_i/h_o=-d_i/d_o so:
\[ \frac{d_i}{d_o} = \frac{f}{d_o -f } \]

Rearranging:

\[ \frac{1}{d_o} + \frac{1}{d_i} = \frac{1}{f} \]

MIRROR EQUATION

Examples

Object midway between C and F

Suppose R=+40 cm, so f=R/2=+20 cm
Place object at d_o=+30 cm

Where will image form?
What will magnification factor be?
Is the image real or virtual?

Object inside focal length, midway between F and V

Suppose R=+30 cm, so f=R/2=+15 cm
Place a 1 cm tall object at d_o=+10 cm

Where will image form?
What will magnification factor be?
Is the image real or virtual?

The image is LARGER than the object but FARTHER AWAY from the eye.
Will it actually LOOK bigger or not?

Apparent or Angular Magnification

Below, the same object is viewed at different distances showing how the angle the object takes up in our field-of-view changes.

Apparent (or Angular) magnification: M = θ_image / θ_object
Normal approximation: θ=(size)/(distance)
(basically the 'arc-length' formula, which gives the angle in radians)
More accurately:
\[ \theta = tan^{-1}(size/distance) \]

Apply to the previous example. Compare m and M for that case.

Example: Concave Mirrors in Telescopes

Backyard Telescope Observing Mars

Closest Distance to Mars: 5.58X10¹⁰ m
Diameter of Mars: 6,784,000 m
Telescope: f=+2.80 m

Where will the image form? (Put film/image-sensor there)
How large will be image of Mars be?

Actual Camera Image Sensor

How 'clear' will that image of Mars be?
How many unique 'pixels' of image data are present?
Image sensor from the camera in a particular 8 MP phone.
  • 3264 X 2448 pixels
  • arranged in a rectangle about (6 mm) X (4 mm)
Implies pixel size of about:
  • 1.8 X 10^-6 m = 1.8 μm = 1.8 micron
Typical camera image sensor pixel size:
  • 1.1 μm to 8.4 μm

Backyard telescope, assuming 1.8 micron pixel size:
  • image size 0.3 mm = 300 microns = 170 pixels
  • Smallest feature size: (6784 km)/170 = 40 km

Hubble Space Telescope

Closest Distance to Mars: 5.58X10¹⁰ m
Diameter of Mars: 6,784,000 m
Telescope: f=+57.60 m
How large will be image of Mars be?

Hubble telescope, assuming 1.8 micron pixel size:
  • image size 7 mm = 7000 microns = 3900 pixels
  • Smallest feature size: (6784 km)/3900 = 1.7 km

ESA Mars Express
Smallest feature: about 2 meters

NOTE: this satellite orbits Mars in a very elliptical path that varies from 250 km to 11500 km, so this represents a an image taken from the low point in the orbit.

Pathfinder (1996)
Smallest feature: a couple of millimeters

Convex Mirror

One option: derive a new equation.
Other: use same equation but adopt a sign convention: treat the 'photon side' as positive.
Convex mirror: treat as a negative radius
Focal length: f=R/2 will then also be negative
Can now use identical equations that worked for concave mirrors.
Magnification factor:
\[ m = \frac{h_i}{h_o} = - \frac{ d_i }{ d_o } \]

Mirror Equation:
\[ \frac{1}{d_o} + \frac{1}{d_i} = \frac{1}{f} \]

Example matching lower figure:
R=-40 cm, so f=-20 cm
Object placed at d_o=+20 cm.
Find image location and size:

Using a ray diagram
Using the mirror equation

Example: Mirrored Sphere Yard Ornament

mirrored sphere of radius 20 cm
Stand 2 meters from sphere
What do we see? (Where is the image? What size? Orientation? Real or virtual?)

Example: Dental Mirror

A dentist uses a curved mirror to view teeth inside the patient's mouth. Suppose she wants an upright image with a magnification of 2.00 when the mirror is 1.25 cm from a tooth. (Treat this problem as though the object and image lie along a straight line.)

What focal length is needed?
Is this a convex or concave mirror?

Now that we know, do a ray diagram.

What will the magnification be?
What will the apparent magnification be if the dentist's eye is 20 cm from the tooth?

Ray Diagrams for Spherical Mirrors
Place an object between C and F in front of a concave mirror (illustrated as an arrow from O to O'). Photons will be flying off from the top of the object in all directions. Let's follow a few of them and see what path each takes: According to our eye, these photons appear to be coming from point I'. We 'see' an upside down version of the object (the 'image') as if it were actually located at that point.
Principal Rays
Photons from a point are flying out at 'all' angles, and all will pass through a corresponding image point I'. There are basically FOUR whose paths are easy to draw, called PRINCIPAL RAYS, producing what is called a RAY DIAGRAM. A ray parallel to the axis reflects through F. (useful) A ray through F reflects into a ray parallel to the axis. (useful) A ray that's a radial (as if it came from point C) reflects right back along the same line. (rarely useful) (Not shown above.) A ray that hits the vertex V (labelled A in the figure) reflects such that the angle below the axis is the same as the incoming ray above the axis. (useful)

Mirror Equation and Magnification
Let's use a few of these rays to convert the ray diagram into an equation that relates the object and image locations.

Using the vertex ray (O'-A'-I') the yellow and green triangles are similar triangles. \[ \frac{h_o}{d_o} = \frac{ \| h_i \| }{ d_i } \] Sign convention: if h_o is a positive number, then h_i here should be considered negative so h_i = -\|h_i\|, leading to: \[ \frac{h_o}{d_o} = \frac{ - h_i }{ d_i } \] Flip that over and rearrange a bit: \[ \frac{h_i}{h_o} = - \frac{ d_i }{ d_o } \] The ratio of image height to object height is called the magnification of the mirror, so:
\[ m = \frac{h_i}{h_o} = - \frac{ d_i }{ d_o } \]	MAGNIFICATION
Where will the image be located? Let's use a different ray and another pair of similar triangles:
Using the ray that passes through F (O'-F-B-I') the yellow and green triangles are similar triangles. Comparing the ratio of the height to the base for each triangle: \[ \frac{h_o}{d_o - f} = \frac{ - h_i }{ f } \] Rearranging: \[ \frac{h_i}{h_o} = - \frac{f}{ d_o - f} \] The left side is the magnification m which we found was also equal to m=h_i/h_o=-d_i/d_o so: \[ \frac{d_i}{d_o} = \frac{f}{d_o -f } \] Rearranging:
\[ \frac{1}{d_o} + \frac{1}{d_i} = \frac{1}{f} \]	MIRROR EQUATION

Examples
Object midway between C and F Suppose R=+40 cm, so f=R/2=+20 cm Place object at d_o=+30 cm Where will image form? What will magnification factor be? Is the image real or virtual?
Object inside focal length, midway between F and V Suppose R=+30 cm, so f=R/2=+15 cm Place a 1 cm tall object at d_o=+10 cm Where will image form? What will magnification factor be? Is the image real or virtual?
The image is LARGER than the object but FARTHER AWAY from the eye. Will it actually LOOK bigger or not?

Apparent or Angular Magnification
Below, the same object is viewed at different distances showing how the angle the object takes up in our field-of-view changes.

Apparent (or Angular) magnification: M = θ_image / θ_object Normal approximation: θ=(size)/(distance) (basically the 'arc-length' formula, which gives the angle in radians) More accurately: \[ \theta = tan^{-1}(size/distance) \] Apply to the previous example. Compare m and M for that case.