Chapter 32 : Light Reflection and Refraction

Index of Refraction

The speed of light in a vacuum is c=299,792,458 m/s.
The meter is now defined in such a way that this is taken to be an exact value.
(For any work we do in this class, using c=3×10⁸ m/s is close enough.)

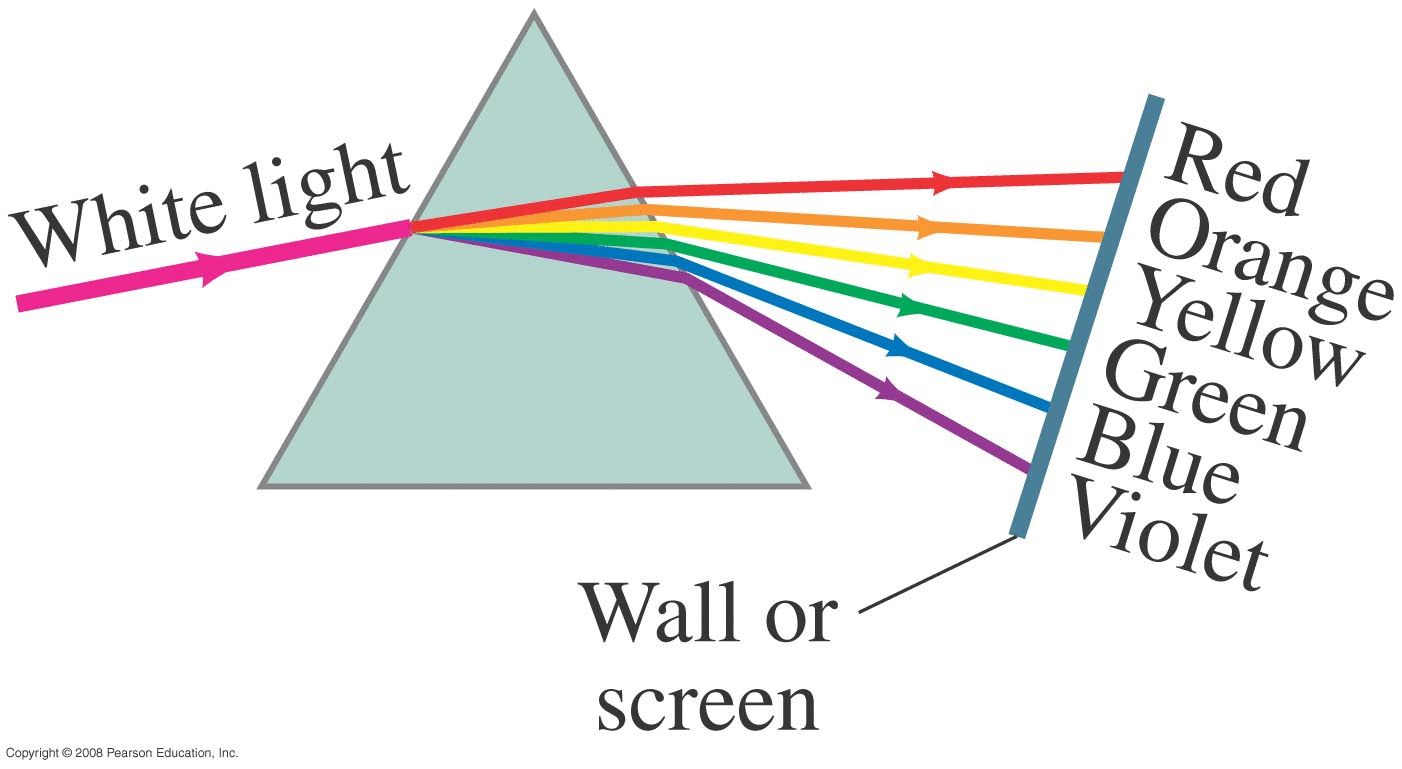
When light travels through other media (air, water, glass, etc) it's speed is less.
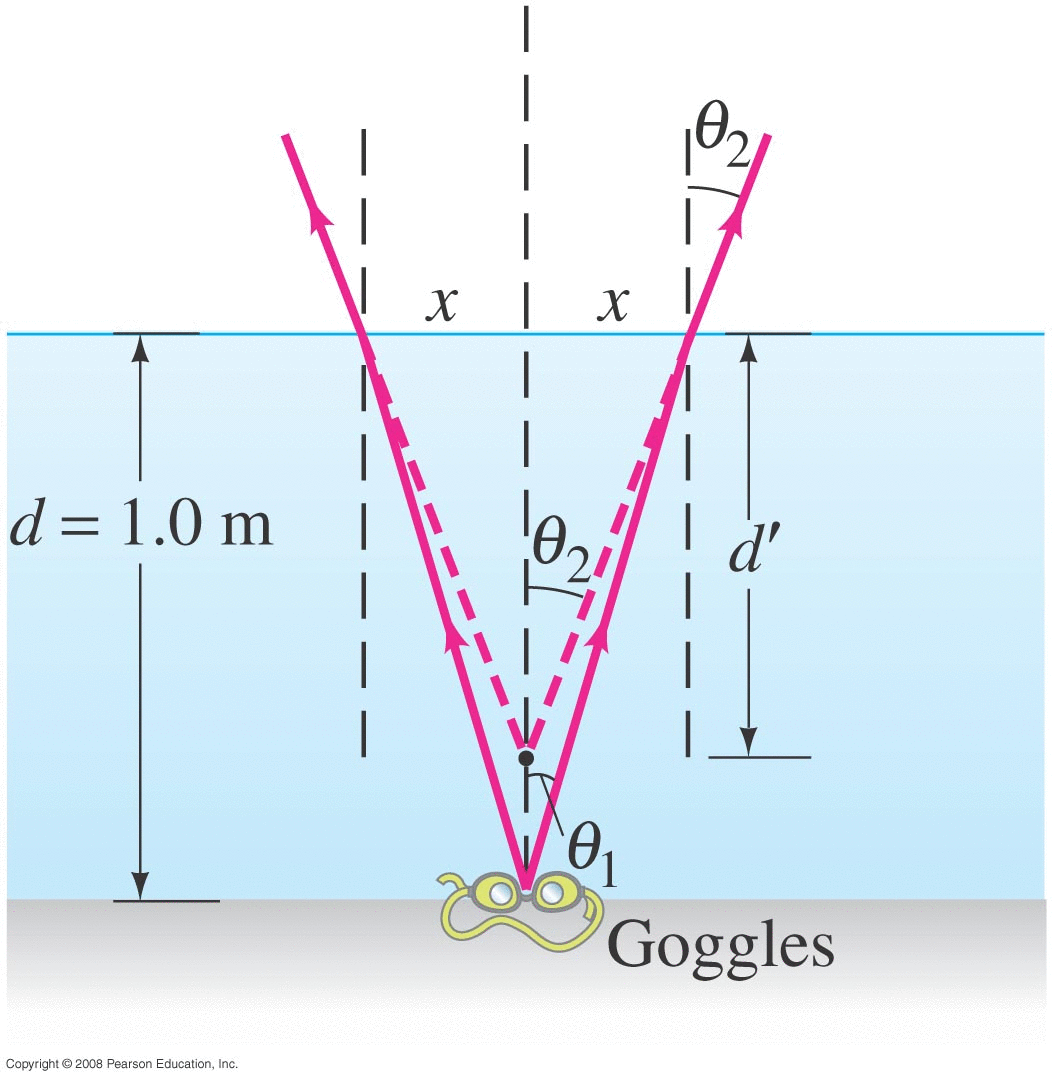
We will see that as a result, when light passes from one medium to another with different wave speeds, it refracts at that interface, changing direction.
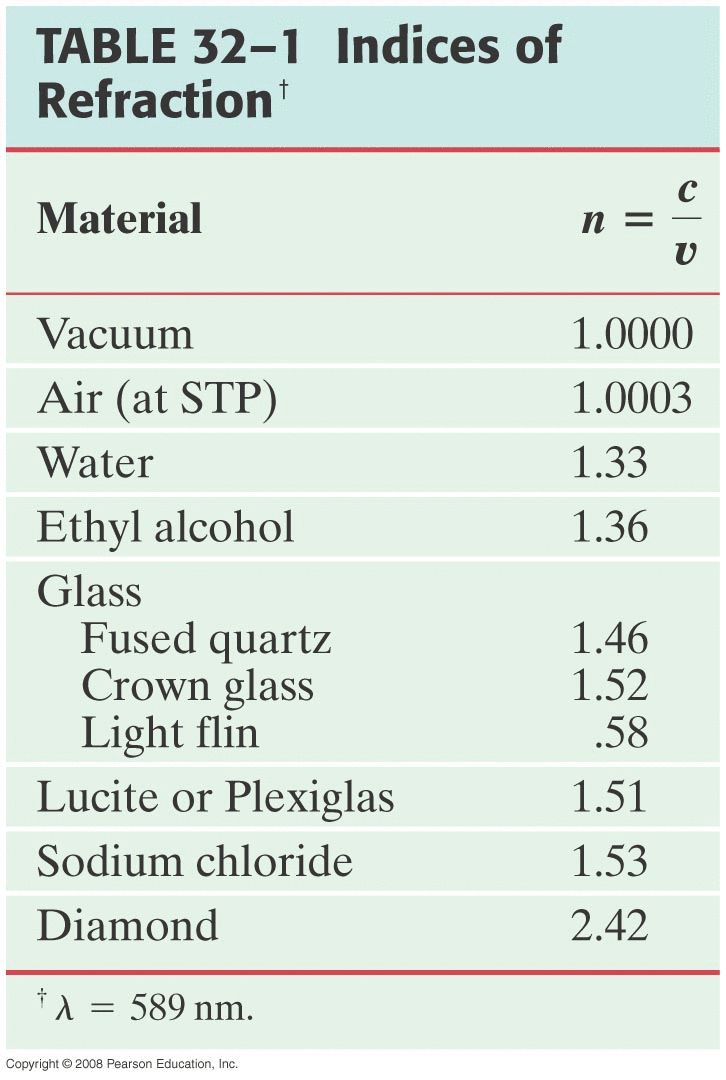
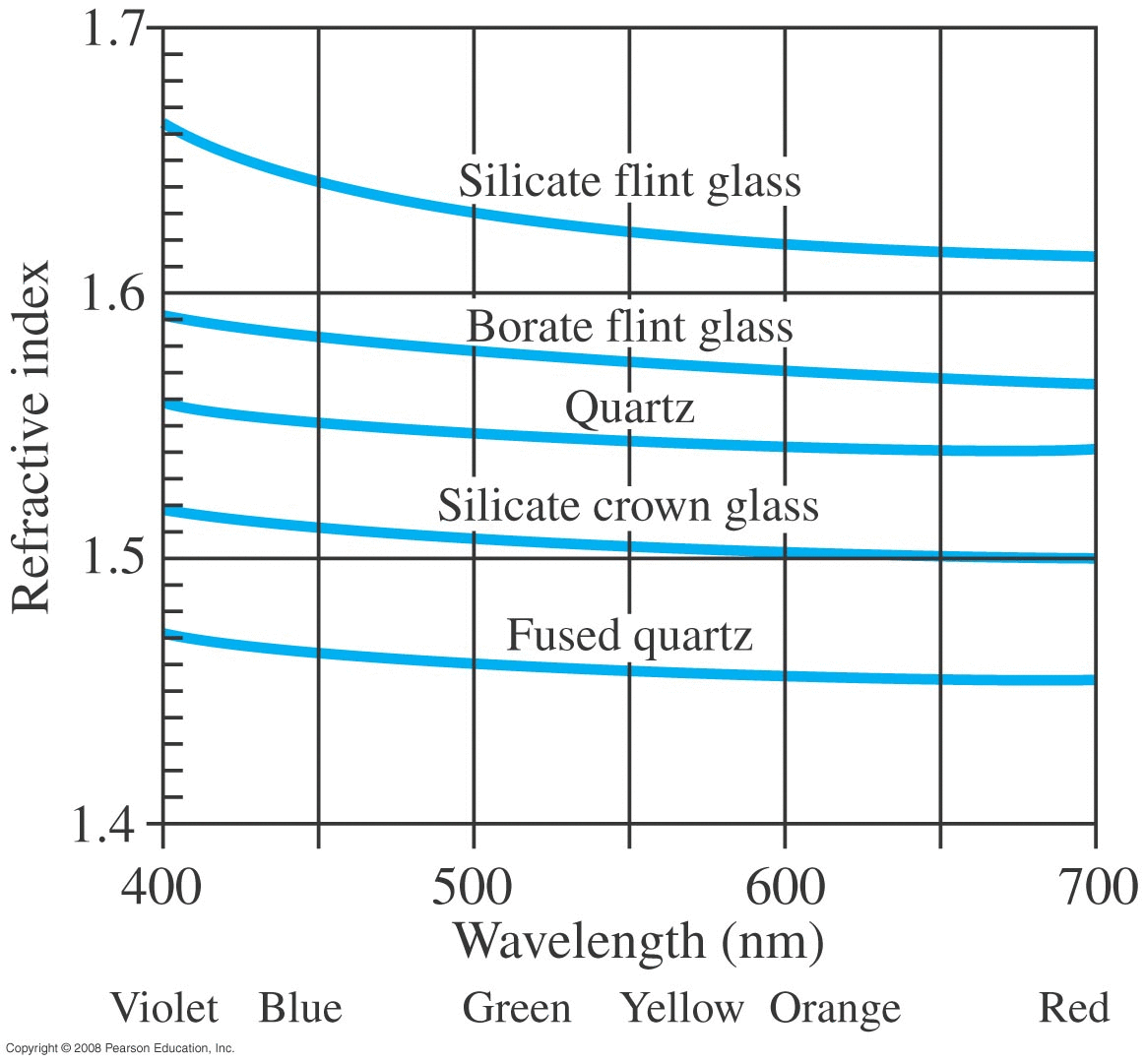
The ratio c/v=n is called the index of refraction for a material.
Since v≤c always, then n≥1 always.

Record so far: n=38.6 (in a lab-created material)

Snell's Law

Rays of light travelling in medium 1 enter medium 2.
The angles θ₁ and θ₂ are measured relative to a normal at the interface.

We'll use this to show how the ray is `refracted' (changes direction) as it moves from a medium of one wave speed to a medium with a different wave speed.
In the case of EM waves, v=c/n so it's more convenient to relate the angles directly to the index of refraction (n) values for the two mediums (rather than using the different speeds of light directly).

Angle of Incidence (θ₁) vs Angle of Refraction (θ₂)

Snell's Law (generic)

\[ \frac{ \sin{\theta_1} }{v_1 } = \frac{ \sin{\theta_2} }{v_2 } \]

Snell's Law (EM waves like light)

\[ n_1 \sin{\theta_1} = n_2 \sin{ \theta_2 } \]

Example: Apparent Pool Depth

Suppose we're looking pretty much straight down into a pool of water where a pair of goggles is resting on the bottom of the pool.
How far away does the bottom of the water appear to be?

Example: Document Under Glass

The same thing occurs if we place a document under a thick layer of glass.
It's the same geometry as above, but n_glass≈1.5 so d'≈⅔d
The glass appears to be only about 2/3 as thick as it actually is.

(The original derivation assumed we're looking nearly straight down through the medium. If not, the image location moves further up and shifts slightly to the side.)

Apparent thickness as viewing angle changes

Visible Spectrum and Dispersion

Electromagnetic waves can occur over a vast range of frequencies, from radio waves to X-rays and beyond.
Our eyes respond to a fairly narrow range of frequencies covering wavelengths between about 400 nm and 750 nm, which our 'optical sensor' perceives as different colors.
(You'll see slightly different ranges quoted in various sources.)

The index of refraction n of real materials varies with wavelength

Resulting in effects like these:

Total Internal Reflection (TIR)

One of the useful features of refraction occurs when waves try to travel from a lower speed medium (i.e. higher n) into a higher speed medium (i.e. a lower n).

We'll see that not all the light from the source can escape into the upper medium, instead becoming trapped in the first medium.

Example: Pool Lights

Suppose we have a pool that is 3 m deep, filled with water, and the item marked `Source' in the above figure is a light on the bottom of the pool.
Find the critical angle and determine how large the circle of light will be on the surface of the pool.

(We'll address the changing color of the 'water feature' stream of water later.)

Example: Glass Prisms in Binoculars

The more expensive types of binoculars use clear glass prisms instead of mirrors.
Follow the ray along the bottom of the figure: what happens to those photons when they encounter the back side of the prism and try to exit?
Assume n_glass=1.5 here.

Fiberoptic Internet

Medical Fiberoptics

Pool Water Feature Revisited

Looking back at the water feature (stream of water) in the pool picture earlier, why is it lit up?
Light travelling inside the water 'mostly' internally reflects, but the outer surface of the stream is not perfectly smooth and a small fraction of the light will fail to TIR and be able to exit all along the stream.

Why does the stream of water in the pool water-feature change color?

Index of Refraction of Water
Red: λ=700 nm θ_c=48.7^o
Purple: λ=400 nm θ_c=47.8^o

Sound Refraction

Suppose we have a source of sound (speaker, explosion, ...) that is above the water.
What happens to this sound when it enters the water?
• v_sound≈343 m/s (in air)
• v_sound≈1500 m/s (in water)

What if the source of sound is under water?
What happens to the sound when it refracts into the air?

Snell's Law

Rays of light travelling in medium 1 enter medium 2. The angles θ₁ and θ₂ are measured relative to a normal at the interface. We'll use this to show how the ray is `refracted' (changes direction) as it moves from a medium of one wave speed to a medium with a different wave speed. In the case of EM waves, v=c/n so it's more convenient to relate the angles directly to the index of refraction (n) values for the two mediums (rather than using the different speeds of light directly).
Angle of Incidence (θ₁) vs Angle of Refraction (θ₂)
Snell's Law (generic)	\[ \frac{ \sin{\theta_1} }{v_1 } = \frac{ \sin{\theta_2} }{v_2 } \]
Snell's Law (EM waves like light)	\[ n_1 \sin{\theta_1} = n_2 \sin{ \theta_2 } \]

Visible Spectrum and Dispersion
Electromagnetic waves can occur over a vast range of frequencies, from radio waves to X-rays and beyond. Our eyes respond to a fairly narrow range of frequencies covering wavelengths between about 400 nm and 750 nm, which our 'optical sensor' perceives as different colors. (You'll see slightly different ranges quoted in various sources.)
The index of refraction n of real materials varies with wavelength
Resulting in effects like these:

Total Internal Reflection (TIR)
One of the useful features of refraction occurs when waves try to travel from a lower speed medium (i.e. higher n) into a higher speed medium (i.e. a lower n).

We'll see that not all the light from the source can escape into the upper medium, instead becoming trapped in the first medium.

Example: Glass Prisms in Binoculars
The more expensive types of binoculars use clear glass prisms instead of mirrors. Follow the ray along the bottom of the figure: what happens to those photons when they encounter the back side of the prism and try to exit? Assume n_glass=1.5 here.
Fiberoptic Internet	Medical Fiberoptics