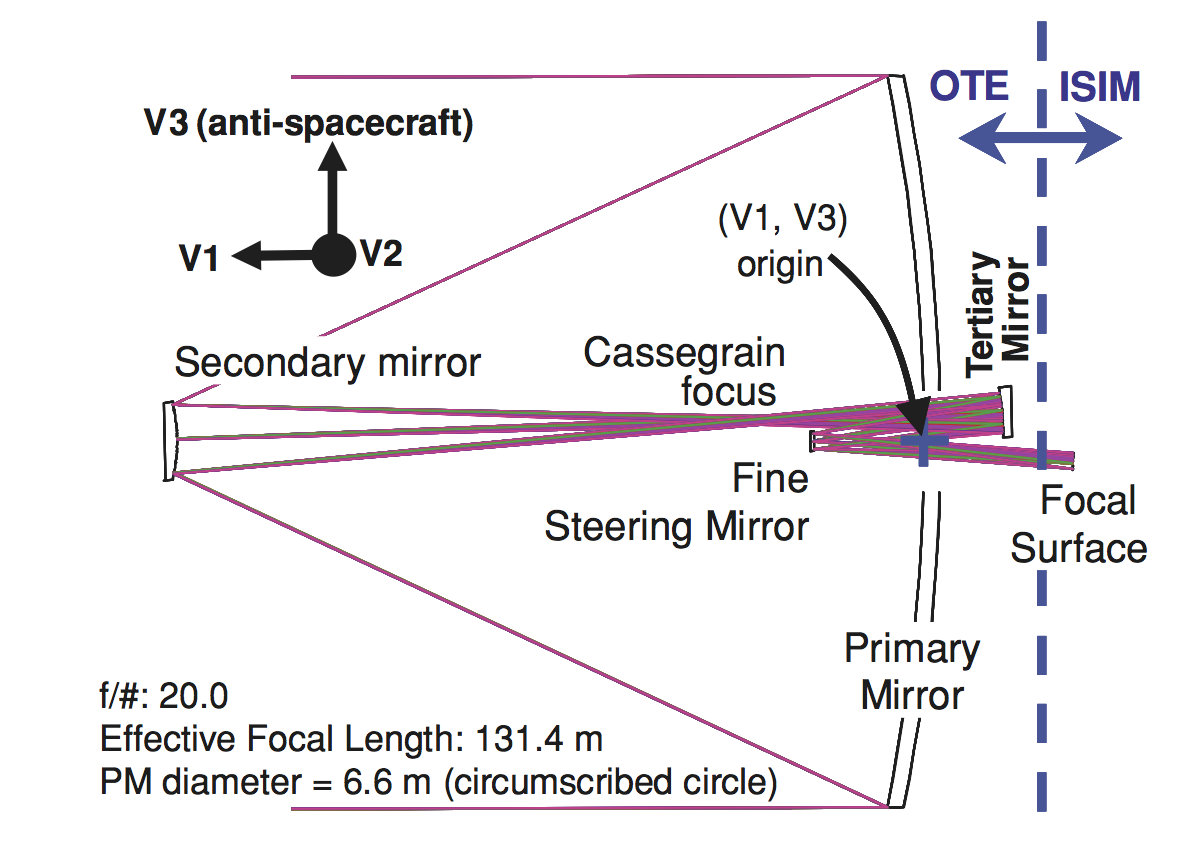
Multiple Mirrors
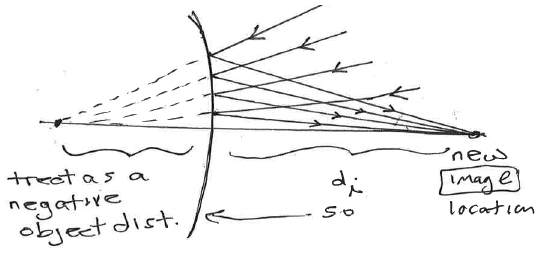
Mirror Equation: \[ \frac{1}{d_o} + \frac{1}{d_i} = \frac{1}{f} \] Consider a telescope (like Hubble) that uses a mirror to image planets and stars that are extremely far away (millions of km or far farther). do>>f (to many orders of magnitude) so the image distance will essentially just be di=f to many significant figures. m=hi/ho and m=-di/do so: \[ h_i = m h_o = ( -\frac{d_i}{d_o} ) h_o = -f * \frac{h_o}{d_o} \] The fraction we can't do anything about: it's (say) the diameter of Mars, divided by the distance from the telescope to Mars. We want the image to be as large as possible, so we want f to be as large as possible. 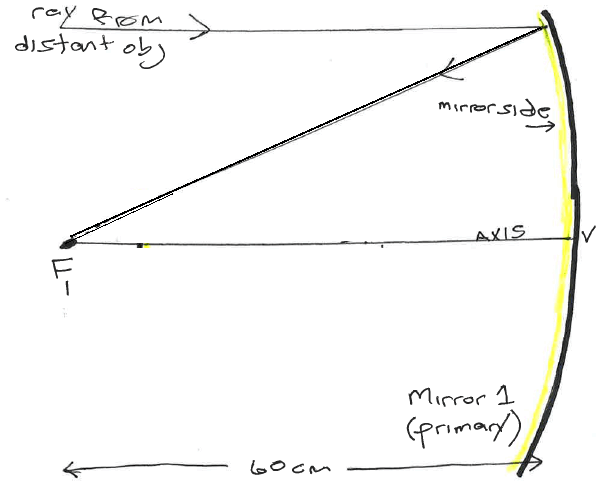Hubble has a focal length of about 57.6 meters, for example. 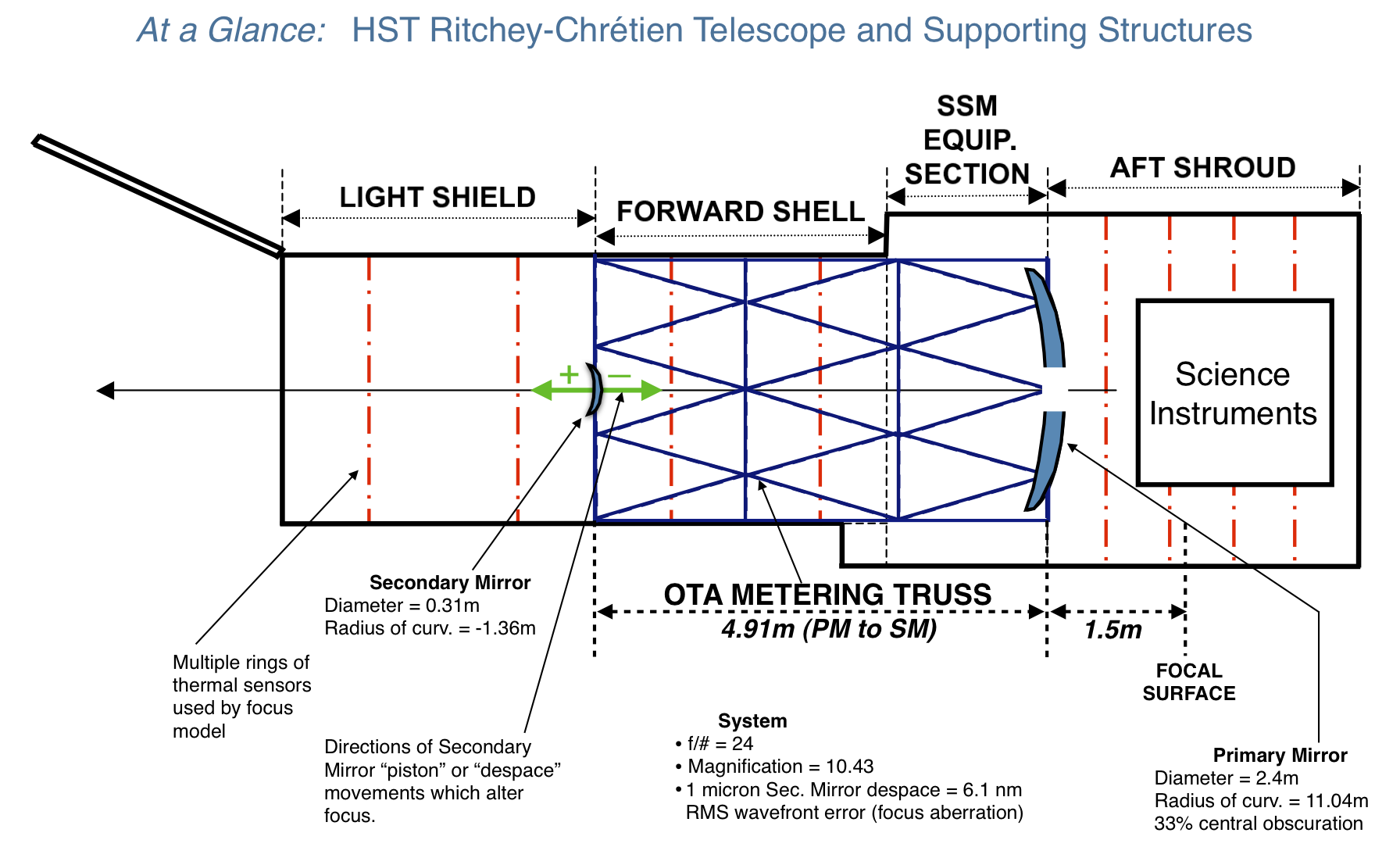That implies that the telescope needs to be that large though to include both the mirror and the 'film' (image sensor). 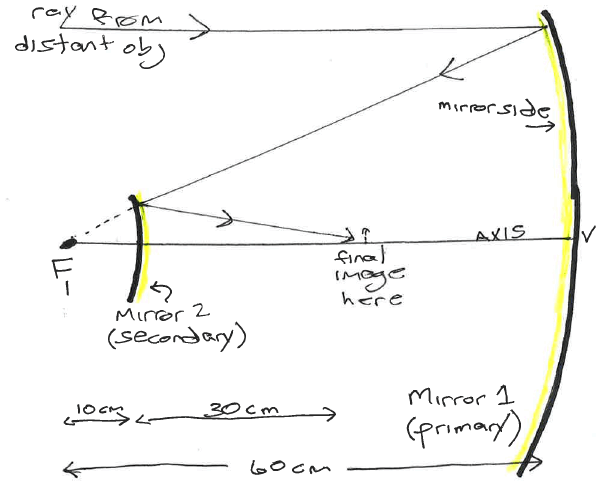The actual length of the Hubble telescope is only about 13.3 meters though. How?
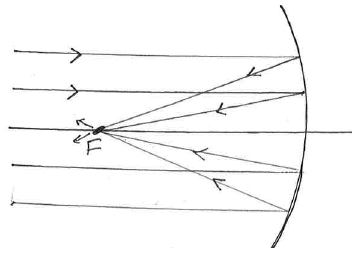
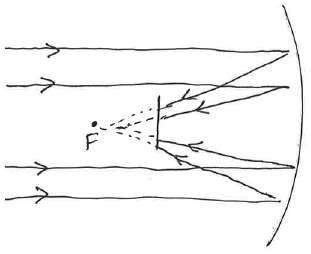
Light from a distant object hitting a concave mirror.	A (flat) mirror placed in the way.
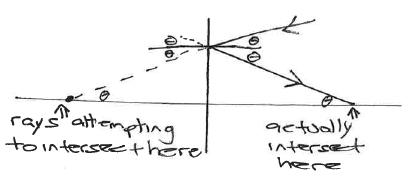
What happens to the rays (photons)?	Effect with a curved 'secondary' mirror.

 

Telescope Double-Mirror Geometry
Mirror Equation: \[ \frac{1}{d_o} + \frac{1}{d_i} = \frac{1}{f} \] The focal length of telescopes is typically 100 meters or less (usually much less). If do is vastly larger than the focal length, the image forms essentially at di=f
Suppose f=+60 cm and we're looking at Mars (with do measured in tens of millions of kilometers at best). Then (here, all distances are measured in centimeters and I'll drop the units): \[ d_i = f = 60 \] \[ m = h_i/h_o = -d_i/d_o = -d_i/d_{mars} = -60/d_{mars} \] \[ h_i = -60 h_{mars}/d_{mars} \]   Place a secondary mirror (convex, with f=-30 cm) 10 cm to the right of the focal point of the primary mirror.   • Where will the final image form?   • Will it be real or virtual? Inverted or upright?   • How large will the final image be?   • What is the effective focal length here?

 

Hubble Space Two-Mirror Arrangement

Focal length: 57.6 m Physical length: 13.3 m

JWST Three-Mirror Arrangement

Focal length: 131.4 m Physical length: about 10 m (excluding sun-shade)