Ch 33 : Lenses and Optical Instruments
Lenses fall into two general categories: converging and diverging
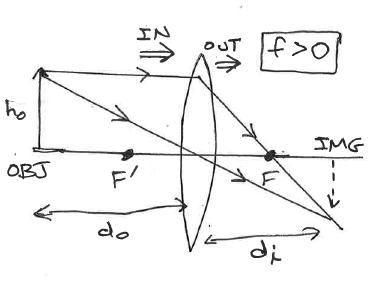
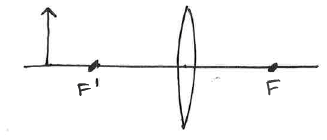
Converging Lens
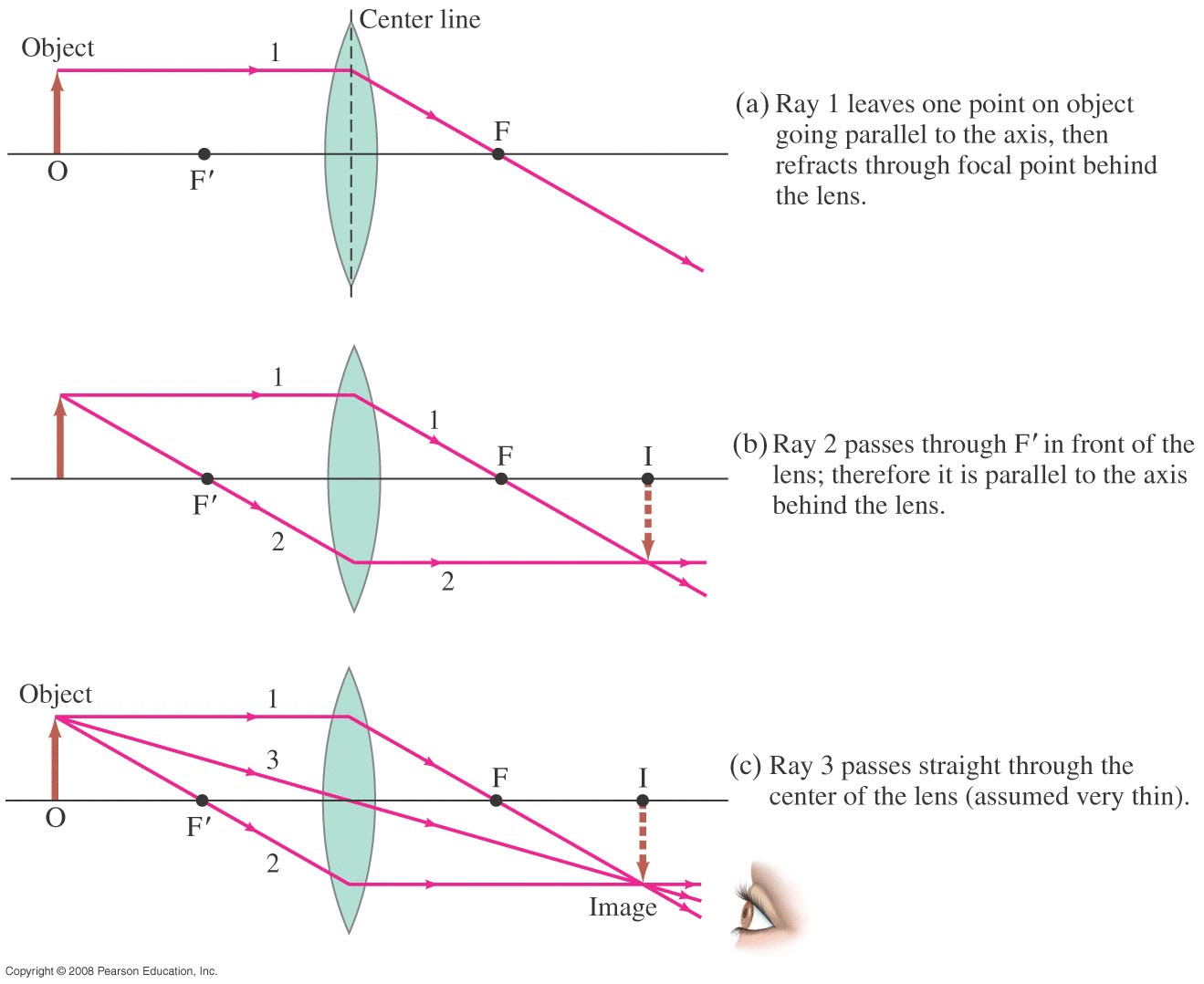
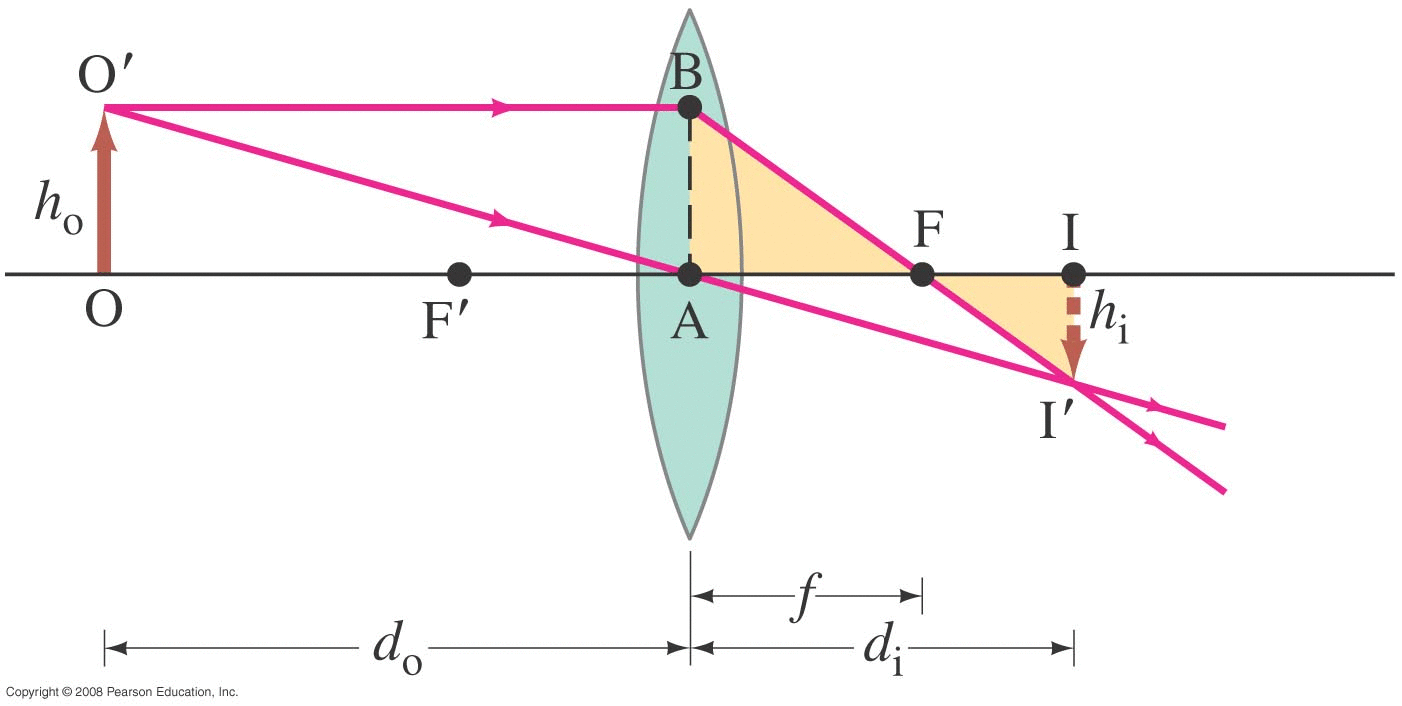
Light from a distance object (i.e. parallel rays) will converge at a point on the other side (the 'outgoing ray' side) of the lens.
We didn't prove this but parallel rays coming in at some angle 'off axis' will also focus at a point, and these points form the focal plane which turns out to be a plane perpendicular to the axis.
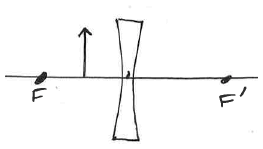
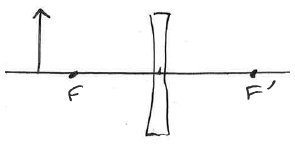
Diverging Lens
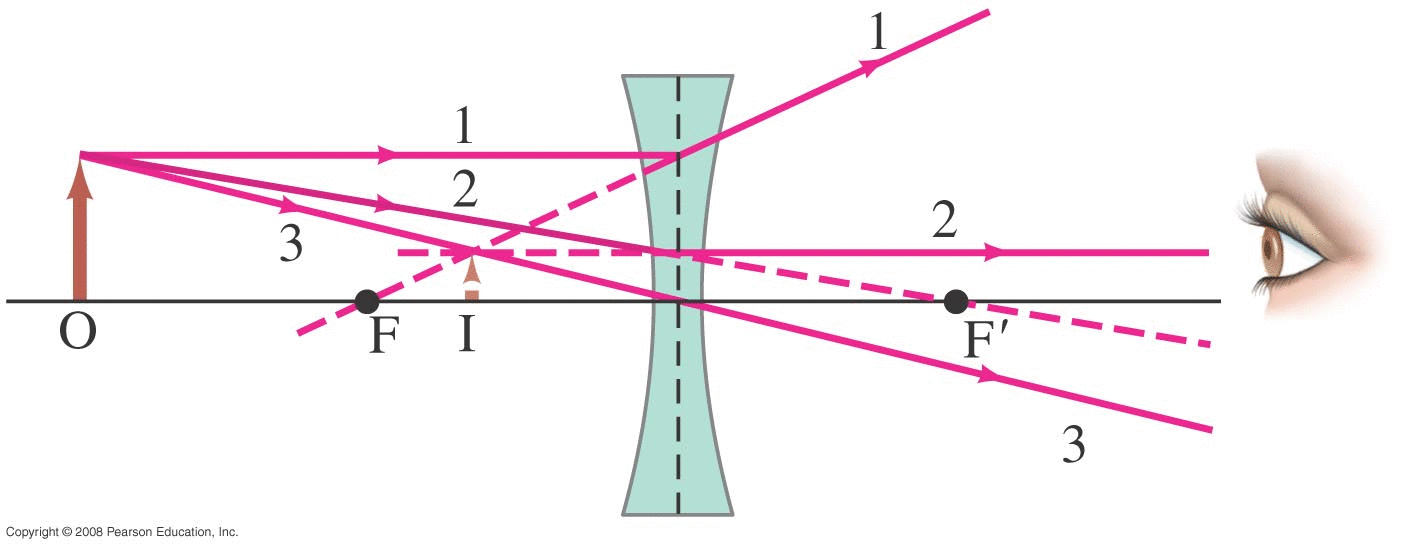
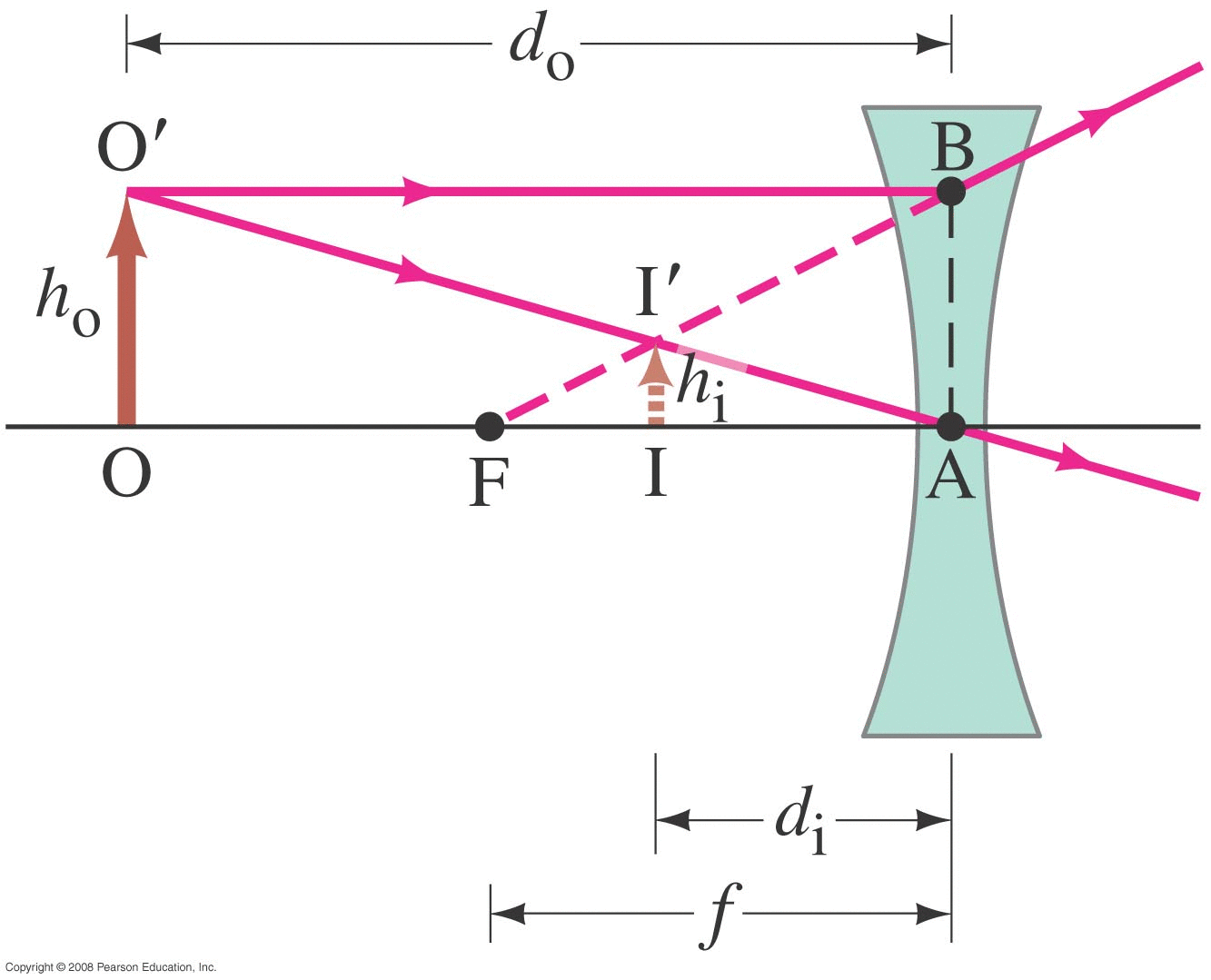
Light from a distance object (i.e. parallel rays) will diverge as they pass through the lens, appearing to come from a point that isn't on the outgoing ray side but rather on the incoming ray side.
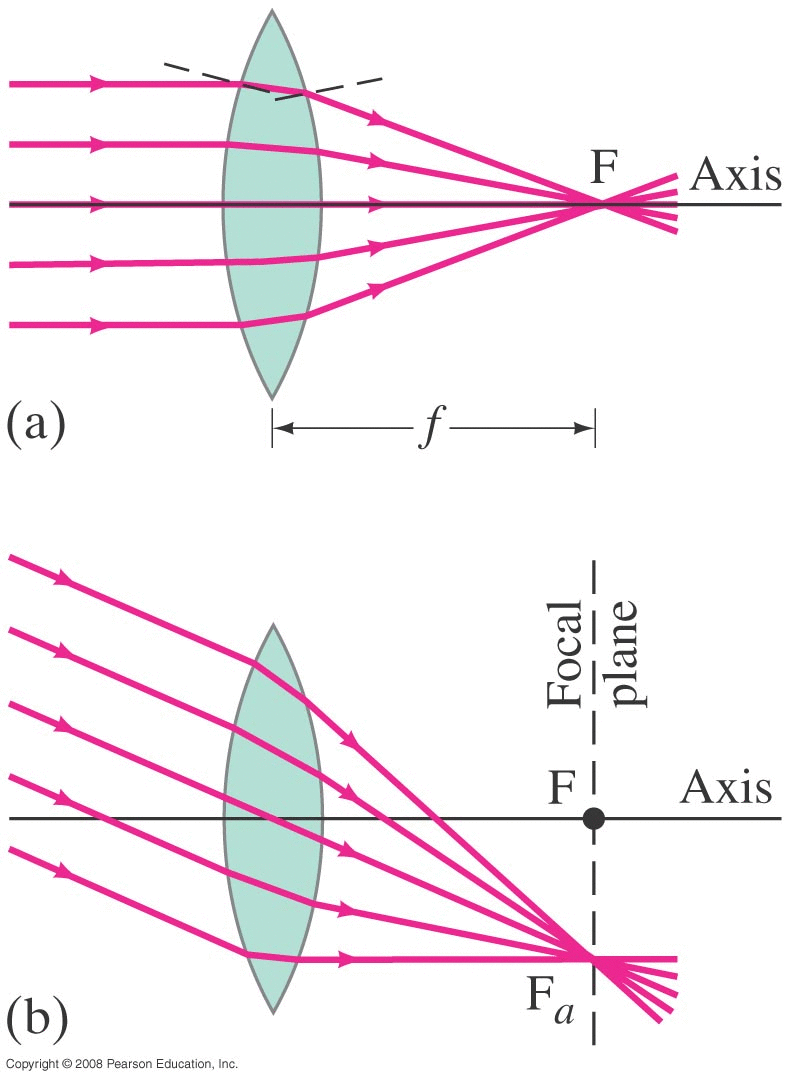
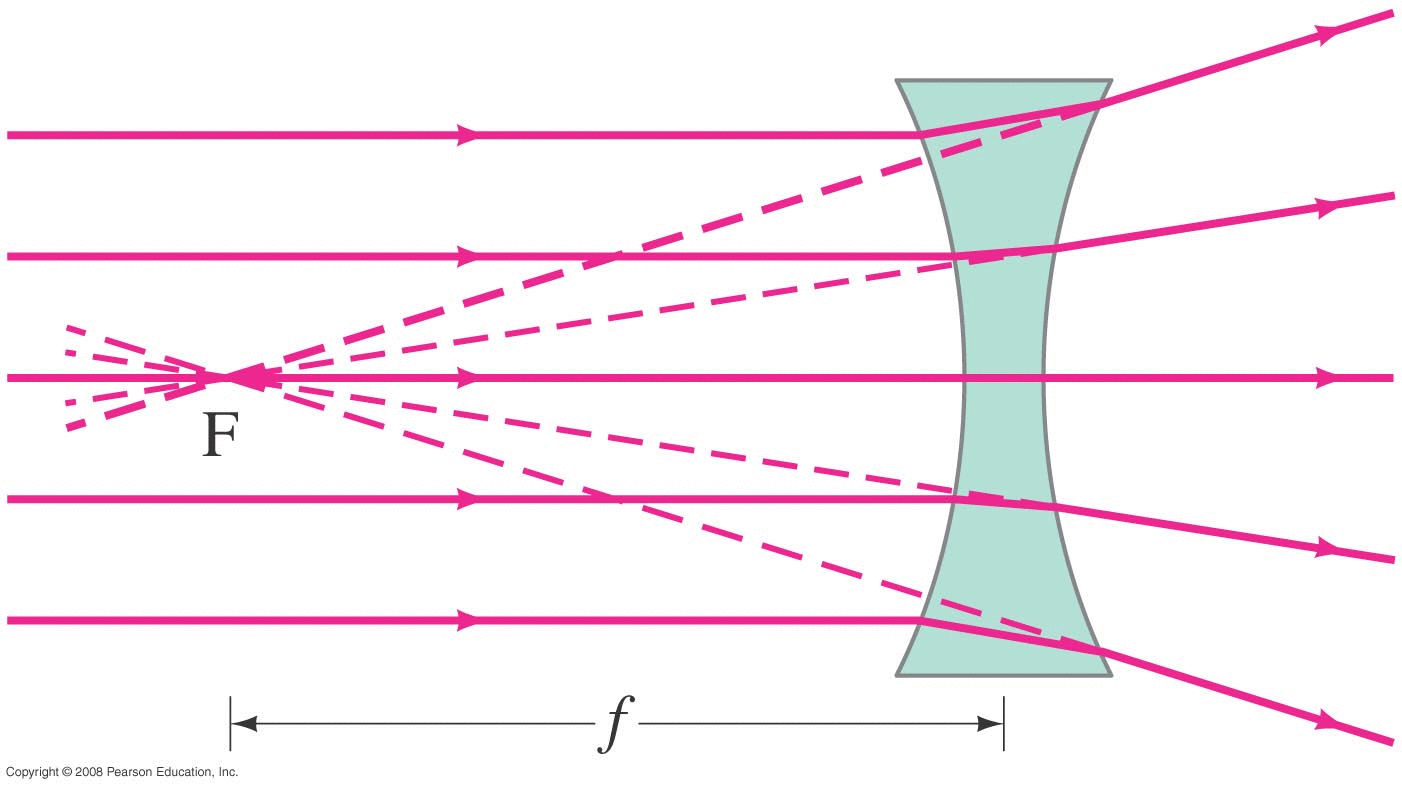
Terminology/Convention
Optometrists/ophthalmologists typically don't quote focal length (f) directly but use a term called the power of the lens:
\[ P=1/f \hspace{2em} (with~f~measured~in~meters) \]
Technically P will have units of inverse meters (m-1) but in the field this is called a diopter (D).
Example: a converging lens with f=+20 cm has a lens power of
P=1/(0.2 m) = +5 m-1 = +5 D