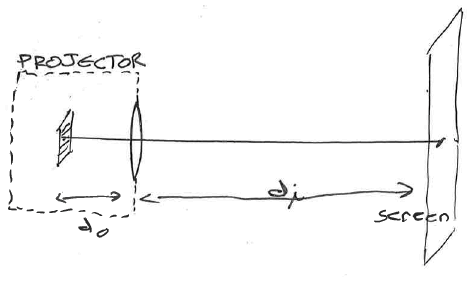
Lens Design : Classroom Projector
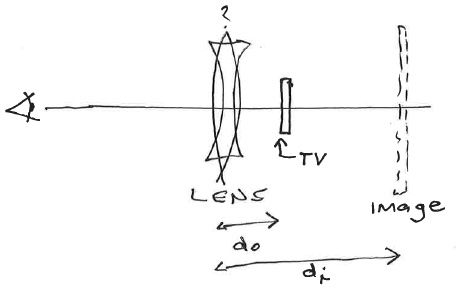
The previous generation of classroom projector had a small screen inside that was magnified by a lens, with the final image forming on the drop-down screen.  • What lens focal length is needed to do this?  • The final image is about 3 meters across, so how large is the internal screen (the 'object')?
Estimates:  • distance from internal screen to lens: 10 cm  • distance from lens to projection screen: : 5 m   Tools: \[ \frac{1}{d_o} + \frac{1}{d_i} = \frac{1}{f} \] \[ m = \frac{h_i}{h_o} = -\frac{d_i}{d_o} \]

 

Combinations of Lenses
Place an object 30 cm to the left of an f=+20 cm converging lens. Determine the location size and nature (real or virtual) of the image.
Add a second f=+20 cm converging lens that is 30 cm to the right of the image being formed by the first lens. Determine the location size and nature (real or virtual) of the final image these two lenses in combination have produced.
(Is there any way to achieve the same result with a single lens?)   \[ \frac{1}{d_o} + \frac{1}{d_i} = \frac{1}{f} \] \[ m = \frac{h_i}{h_o} = -\frac{d_i}{d_o} \]
Move the second lens so that it's just 30 cm from the first lens. Determine the location size and nature (real or virtual) of the final image these two lenses in combination have produced.
Replace the second lens in the previous example with a diverging lens with f=-20 cm. Determine the location size and nature (real or virtual) of the final image these two lenses in combination have produced.     If the observer places their eye right up to the second lens, what apparent magnification has this 2-lens combination produced?

 

Lensmaker's Equation
Suppose we have a (double convex) lens made of a material of index of refraction n that is embedded in a medium with an index of refraction no.   Judiciously propagating angles and using approximations like sin(θ)≈tan(θ)≈θ we find (see the book for details of the derivation!) that: \[ \frac{1}{f} = ( \frac{n-n_o}{n_o} )( \frac{1}{R_1} + \frac{1}{R_2} ) \] which is called the Lensmaker's equation and can be rearranged into a sometimes more useful form: \[ f = ( \frac{n_o}{n-n_o} )( \frac{ R_1 R_2 }{ R_1 + R_2 } ) \]
The radii follow a sign convention illustrated below. This book (and many others, but not all) use a convention that for a double-convex lens, both R values will be positive. For such a lens, the center of curvature of each side is over on the opposite side.   Double Convex : both R positive, so f will be positive (converging lens) Double Concave : both R negative, so f will be negative (diverging lens) Plano-convex : R1 positive and R2 is infinity; f is positive (converging) Plano-concave : R1 is negative and R2 is infinity; f is negative (diverging) Meniscus : will do in class (all contacts and eyeglasses use these shapes)   General Result  •  Any lens that is THICKER IN THE MIDDLE will be a CONVERGING lens  •  Any lens that is THINNER IN THE MIDDLE will be a DIVERGING lens

 

Example: TV Magnifier
Early TV screens were very small, so one solution was to add a large lens in front of the screen to create a magnified image. \[ m = \frac{h_i}{h_o} = -\frac{d_i}{d_o} \] We can't easily turn the TV upside down, so if we want a positive image height, we'll need a negative image distance (i.e. a virtual image.
Example	The geometry we're working with.
Suppose we're sitting 2 meters in front of the TV and we place the lens 15 cm in front of the TV and we want a magnification of m=1.5.  •  Where will the image be?  •  What focal length will the lens need to have?  •  What will the apparent magnification be?  •  If we use a double-convex shape with the same R on each side, what does R need to be? (Assume the lens is made of glass with n=1.5)  •  How thick will the lens be? (Assume the TV has a roughly 12 inch screen size, so ho is about 30 cm (making hi about 45 cm).   So how did these things actually work?

 

Fresnel Lens
We don't need the 'insides' of the lens: all our equations assume the lens is 'thin' so what if we just keep the left and right surfaces of the lens where the refraction is happening.
Cross-section	Unfortunate Side-effect	Light House
Cheap-ish Magnifiers
Really Cheap Magnifiers ('bookmarks' given away at trade shows)