Chapter 33 : Lenses and Optical Instruments

(33-6) The Human Eye; Vision Correction

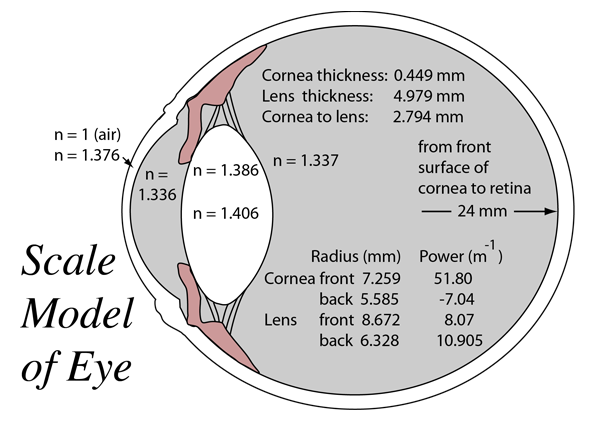
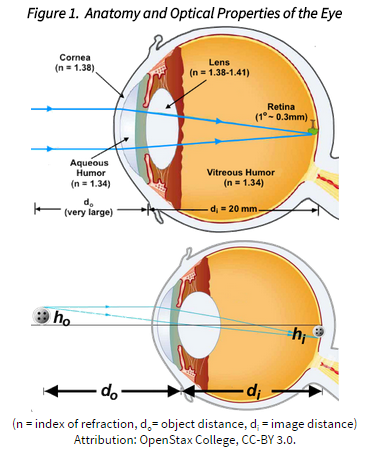
Typical human eye:
• refraction occurs at each interface
• most occurs at the air-cornea interface (largest n contrast)

In a 'relaxed eye' light from far away (i.e. limit as d_o goes to infinity) focuses on the retina, about 24 mm from the front surface of the cornea.
f = 24 mm P=1/f=1/(0.024 m) = +41.7 D
(2/3 of that occurs at the front surface of the eye)

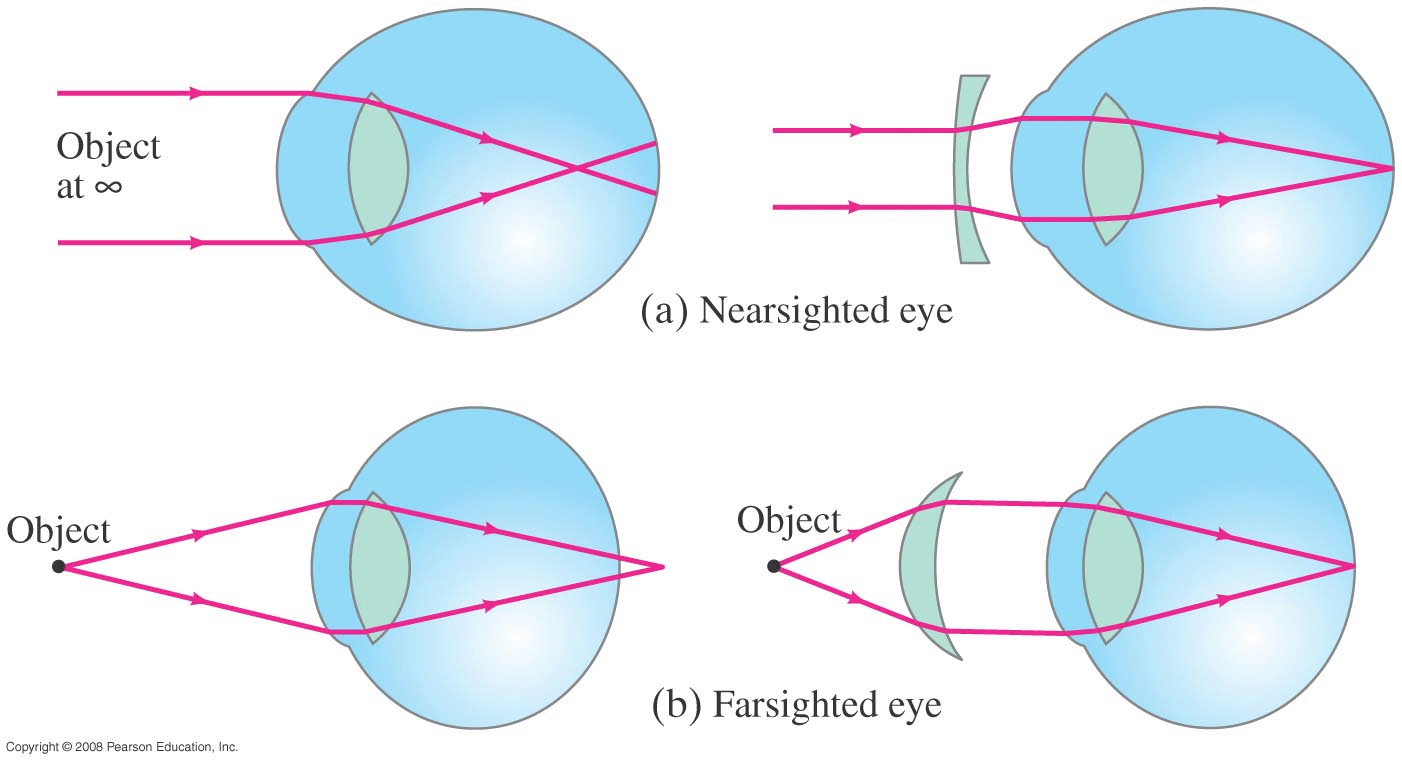
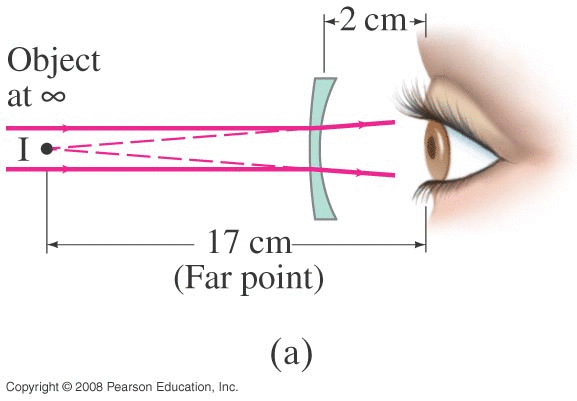
FAR POINT : the distance to the farthest object you can still focus on. For a 'normal eye' that is effectively infinity. (Eye is 'relaxed'.)

NEAR POINT : the distance to the closest object you can still focus on without straining. For a 'normal eye' that is about 25 cm. (Muscles squishing lens.)

ME, pre-cataract surgery : very near-sighted, with a near-point of 10 cm and a far point of about 30 cm.

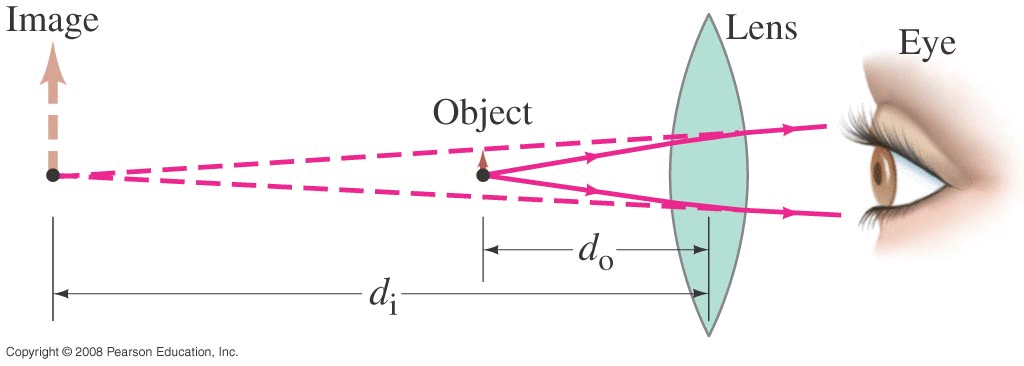
• What overall focal length (and power) would a 'normal' eye have when looking at something 25 cm away?
Note how little the focal length (or power) of the eye changes when focusing on near vs far objects.

Near- and Far-Sightedness

Near-sighted eyes : Upper Left figure : lens not able to focus distant objects onto the retina. Rays converge 'too soon', resulting in blurred image on the retina.
Far-sighted eyes : Lower Left figure: lens can't adjust enough to correctly focus nearby objects onto the retina. Rays are trying to focus behind the retina, resulting in blurred image again.

Typical human eye:
• ~60 million rods (low light, night vision, grey-scale)
• ~3 million cones (color vision; requires brighter light)

Far-Sighted Correction with Contacts

A very far-sighted person, with a near-point of 100 cm wants to be able to read a book held 25 cm from their face.
• What focal length (and lens power) contacts would they need to wear?
• How will adding this lens affect the apparent size of objects?
(NOTE: contacts will be touching the eye, so assume there's no gap between the lens and the eye here.)

Lens is touching the eye: ignore the gap here.

Far-Sighted Correction with Eyeglasses

A very far-sighted person, with a near-point of 100 cm wants to be able to read a book held 25 cm from their face.
• What focal length (and lens power) eyeglasses would they need to wear? (Assume the glasses are located 2 cm away from their eye.)
• How will adding this lens affect the apparent size of objects?

Lens is 2 cm from eye here.

Near-Sighted Correction with Contacts

A near-sighted person, with a far-point of 17 cm wants to be able to view a movie screen 20 meters away.
• What focal length (and lens power) contacts would they need to wear?
• How will adding this lens affect the apparent size of objects on the screen?

Lens is touching the eye: ignore the gap here.

Near-Sighted Correction with Eyeglasses

A near-sighted person, with a far-point of 17 cm wants to be able to view a movie screen 20 meters away.
• What focal length (and lens power) eyeglasses would they need to wear? (Assume the glasses are 2 cm away from their eyes.)
• How will adding this lens affect the apparent size of objects on the screen?

Lens is 2 cm from eye here.

Surgical Lens Replacement

Much of our ability to change our focus between near and far objects comes from muscles that alter the shape of the lens itself.
In cataract surgery, the lens is typically replaced by one that's not able to do that.

My replacement lenses were selected so that an object 80 cm away will focus on the retina (24 mm from the front surface of the eye).
• Where would the image form if I'm reading a book/test held 40 cm away?
• What eyeglasses do I need for reading and grading tests? (Focal length and lens power; assume the glasses are 2 cm from the eyes.)

Option : Multifocal Intraocular Lens

Test 2 Practice problem 33.12

A small object is 25 cm from a diverging lens as shown in the figure.
A converging lens with a focal length of f=12 cm is 30 cm to the right of the diverging lens.
The two-lens system forms a real, inverted image 17 cm to the right of the converging lens.

(a) What must be the focal length of the diverging lens?

(Hint: 'work backwards'.)

(Add: what is the overall magnification factor here? Is the figure consistent?)

Test 2 Practice problem 32.6

Light is incident on an equilateral glass prism at a 45^o angle to one face. (NOTE: those dashed lines are perpendicular to the corresponding faces of this prism.)

Calculate the angle at which light emerges from the opposite face. Assume n=1.54 for the prism.

Equilateral glass prism, so we also know the three corners of this triangle all have 60^o angles.
Other bits to remember:
• triangle: sum of interior angles is 180^o
• quadrilateral: sum of interior angles is 360^o

Test 2 Practice problem 33.6

A diverging lens with f=-14 cm is placed 12 cm to the right of a converging lens with a focal length of f=+18 cm.
An object is placed 33 cm to the left of the converging lens.
   (a) Where will the final image be located?
   (b) Will the image be real or virtual? Upright or inverted?
   (c) What will the overall magnification factor be?

   (If time: if you put your eye up against the diverging lens, what apparent magnification will you perceive?)

Surgical Lens Replacement
Much of our ability to change our focus between near and far objects comes from muscles that alter the shape of the lens itself. In cataract surgery, the lens is typically replaced by one that's not able to do that. My replacement lenses were selected so that an object 80 cm away will focus on the retina (24 mm from the front surface of the eye). • Where would the image form if I'm reading a book/test held 40 cm away? • What eyeglasses do I need for reading and grading tests? (Focal length and lens power; assume the glasses are 2 cm from the eyes.)
Option : Multifocal Intraocular Lens

Test 2 Practice problem 33.12
A small object is 25 cm from a diverging lens as shown in the figure. A converging lens with a focal length of f=12 cm is 30 cm to the right of the diverging lens. The two-lens system forms a real, inverted image 17 cm to the right of the converging lens. (a) What must be the focal length of the diverging lens? (Hint: 'work backwards'.) (Add: what is the overall magnification factor here? Is the figure consistent?)
Test 2 Practice problem 32.6
Light is incident on an equilateral glass prism at a 45^o angle to one face. (NOTE: those dashed lines are perpendicular to the corresponding faces of this prism.) Calculate the angle at which light emerges from the opposite face. Assume n=1.54 for the prism. Equilateral glass prism, so we also know the three corners of this triangle all have 60^o angles. Other bits to remember: • triangle: sum of interior angles is 180^o • quadrilateral: sum of interior angles is 360^o
Test 2 Practice problem 33.6
A diverging lens with f=-14 cm is placed 12 cm to the right of a converging lens with a focal length of f=+18 cm. An object is placed 33 cm to the left of the converging lens. (a) Where will the final image be located? (b) Will the image be real or virtual? Upright or inverted? (c) What will the overall magnification factor be? (If time: if you put your eye up against the diverging lens, what apparent magnification will you perceive?)