Thin Film Interference
If film thickness is t then 'extra path length' is 2t
Might think:
CON : 2t = mλ
DES : 2t = (m+½)λ
BUT NOT THAT SIMPLE!

|
Chapter 34 : The Wave Nature of Light Interference and Polarization |
Thin Film Interference | |
|
If film thickness is t then 'extra path length' is 2t Might think: CON : 2t = mλ DES : 2t = (m+½)λ BUT NOT THAT SIMPLE! |
|
Mechanical Waves Reflecting | |
|
|
|
|
Same effect occurs with EM waves (light, radio waves, etc) when they reflect off an interface: • If the wave encounters a material with a HIGHER n (i.e. a lower speed of light), the reflected ray changes sign (an incoming +sine wave yields a reflected -sine wave). • If the wave encounters a material with a LOWER n (i.e. a higher speed of light), the reflected ray retains the same sign as the incoming wave. |
|
Another Detail | |
|
The wavelength of the light changes depending on the index of refraction. v=λ/T=λf and v=c/n so: λ=v/f=(c/n)/f = (c/f)/n so: λfilm = λo/nfilm where λo is the wavelength in air (well, vacuum)
| |
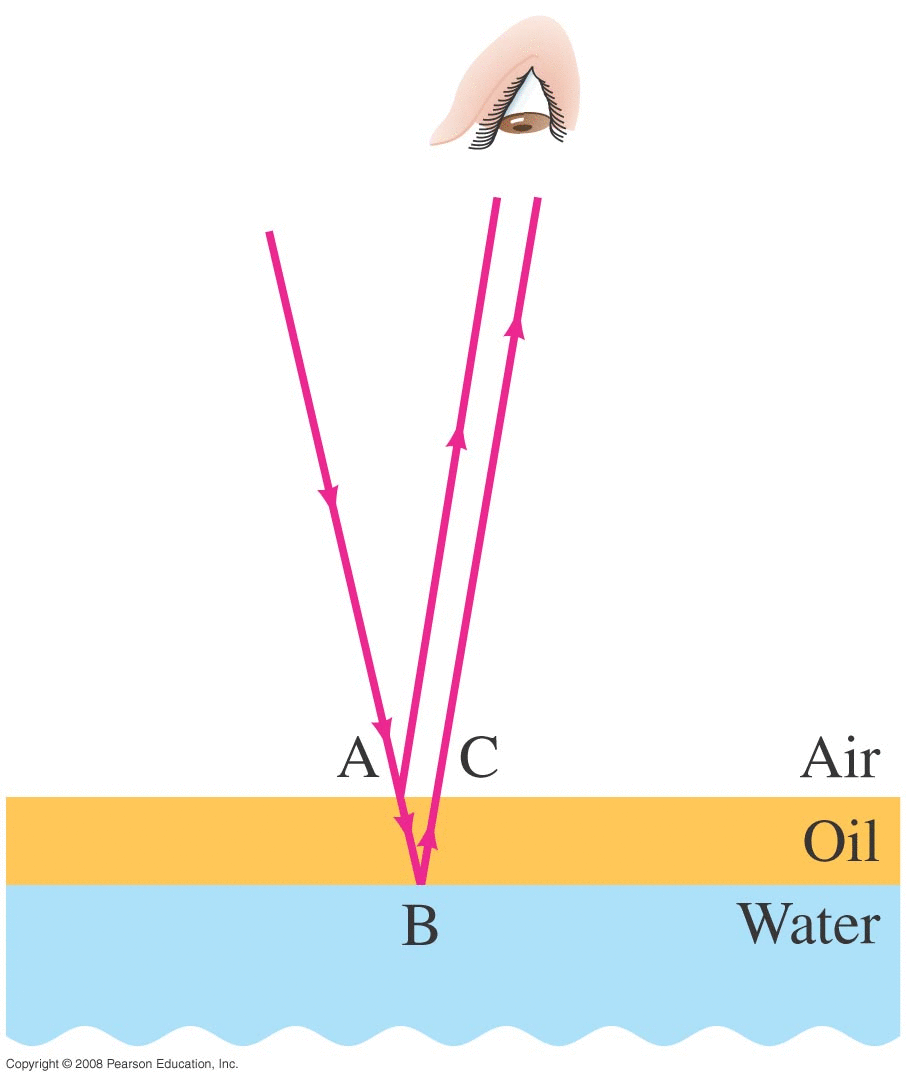
Thin Film of Oil on Water | |
|
Putting it all together now:
Suppose the oil film has a thickness of 1 μm ( 1 X 10-6 m or 1000 nm ) • For what wavelengths (colors) will CONSTRUCTIVE interference occur? • For what wavelengths (colors) will DESTRUCTIVE interference occur? • If one spot looks green (λ=540 nm) how thick is the film at that point?
• What would the equation for CONSTRUCTIVE interference be for this case? \[ 2t = (m+\frac{1}{2})\lambda_{film} \] • What would the equation for DESTRUCTIVE interference be for this case? \[ 2t = (m)\lambda_{film} \]
|
|
Thin Film Interference Examples | ||
 |
 |
 |
Solar Spectrum |
|
|
Solar Film : keep (some) heat from getting into house | |
|
Suppose we want to reduce energy at λ=1000 nm from getting into the house. What window film thickness would do this?
• How do we change that goal into one that matches what our equation represents? • Keeping that wavelength from entering the house means causing constructive interference for the reflected light (i.e. that wavelength is mostly reflected by the film).
Side Effect
• What effect will this thickness have on visible light? What wavelengths will be strongly reflected (and therefore not make it into the house)? How about the opposite - what wavelengths are 'missing' in the reflected light and will therefore be extra bright to people inside the house? |
|
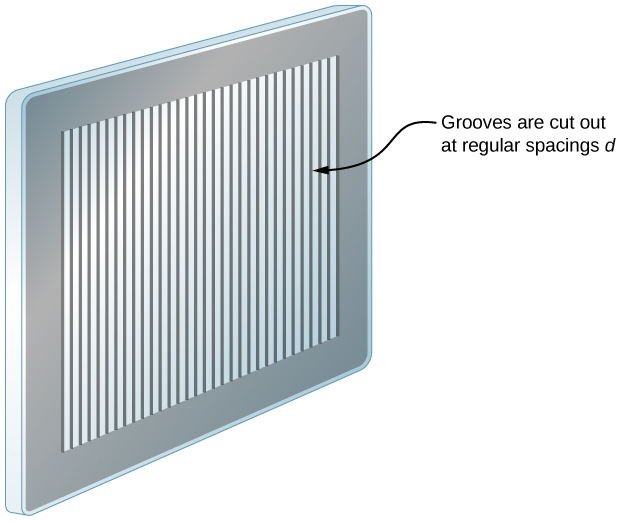
Diffraction Grating (for next lab) |
(See lecture16 for 2-slit interference.)
 |
 |
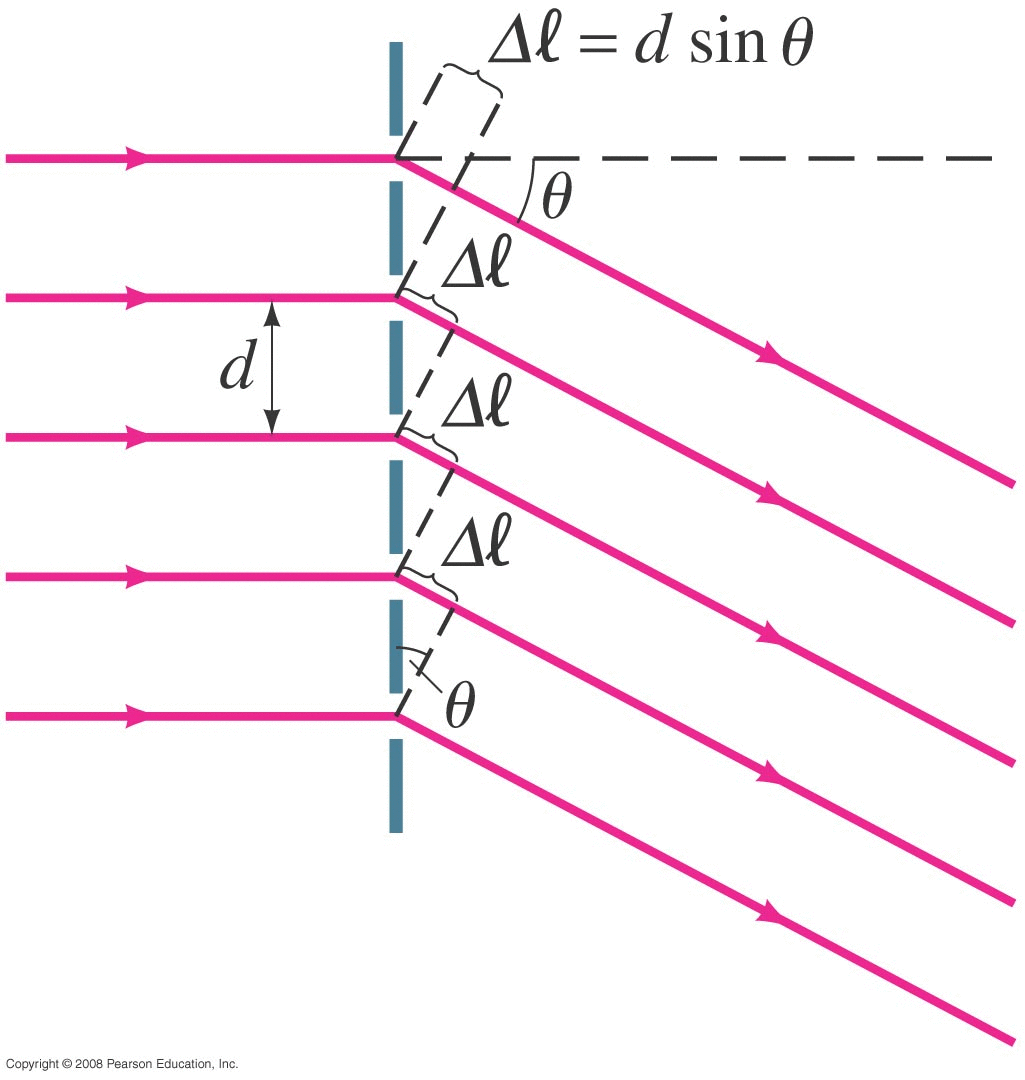
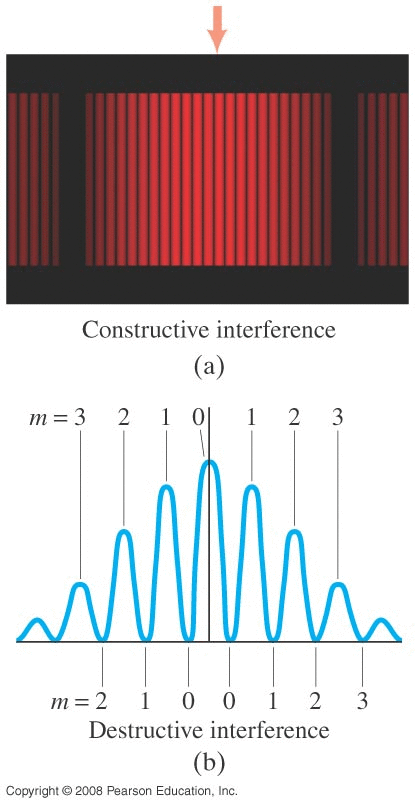
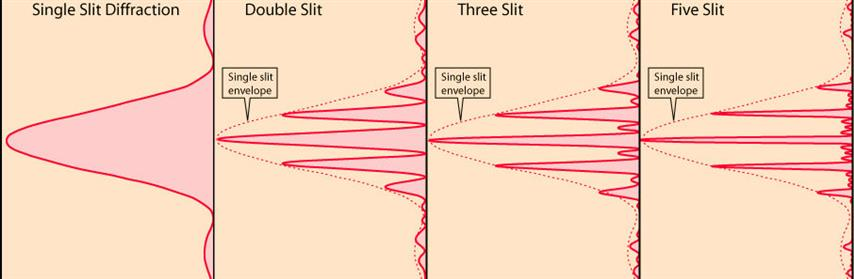

Send white light (the Sun maybe) through a 1000 lines/mm diffraction grating.
• all wavelengths have constructive interference at θ=0
• Look at the range of angles for visible light for m=1
• Look at the range of angles for visible light for m=2
Violet end of spectrum: λ=400 nm
Red end of spectrum: λ=750 nm


