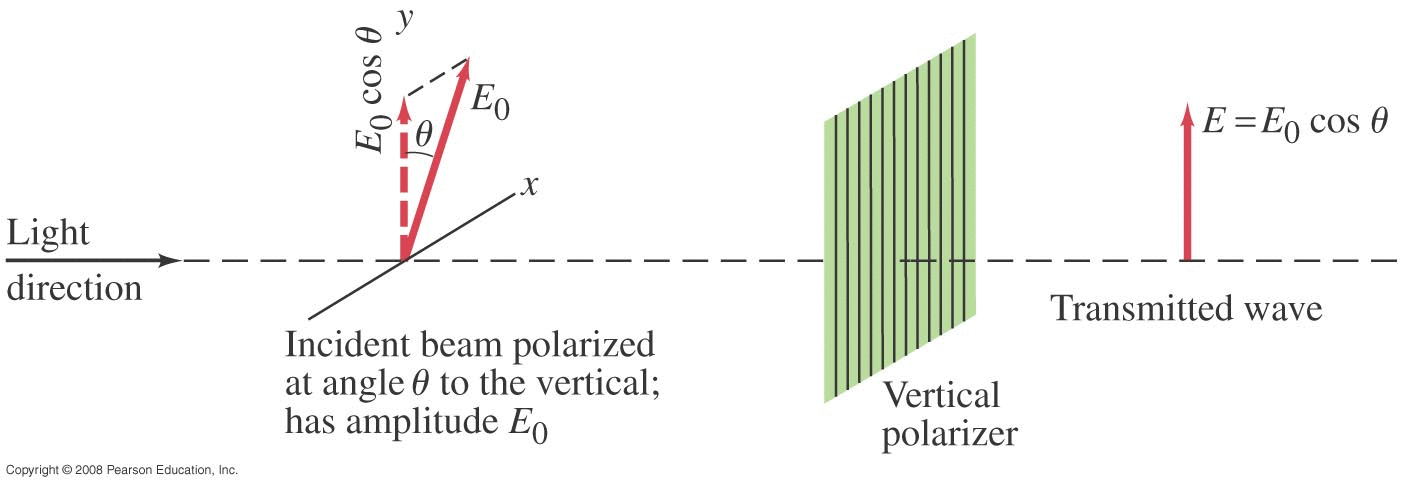
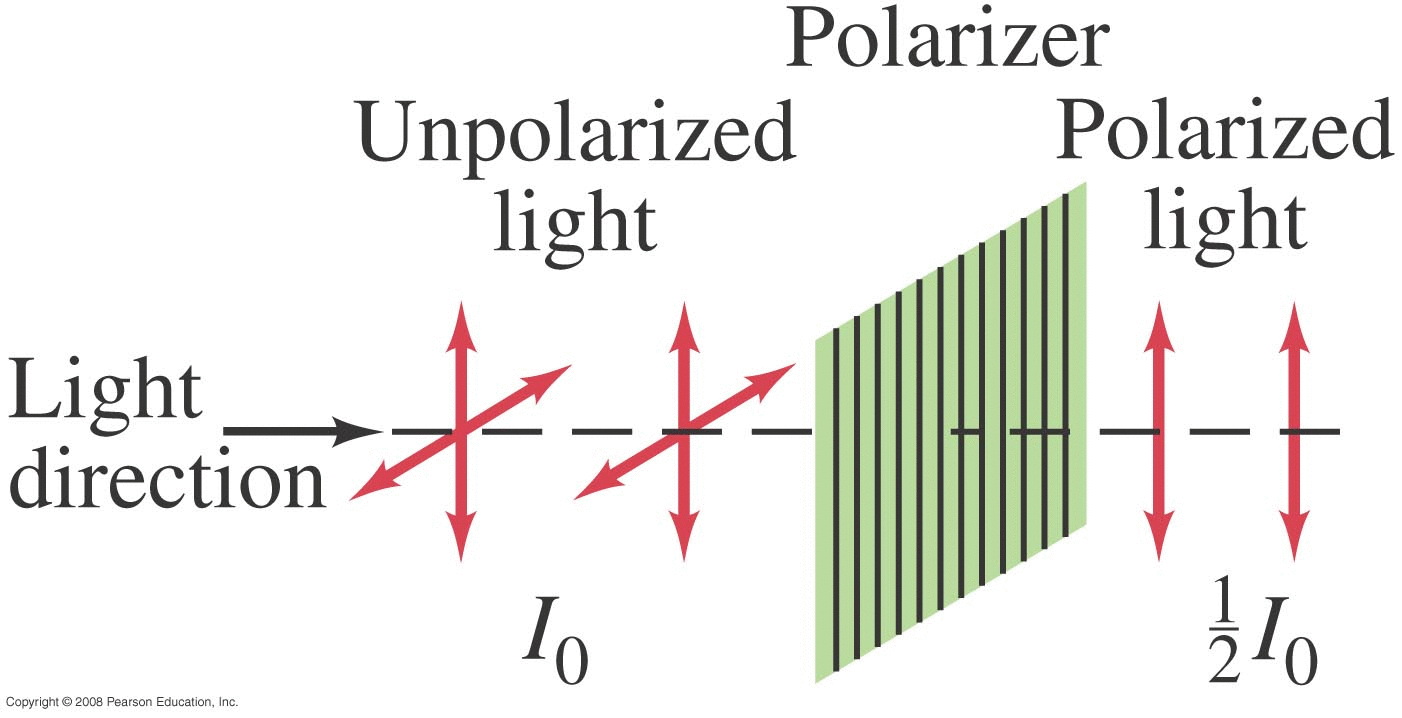
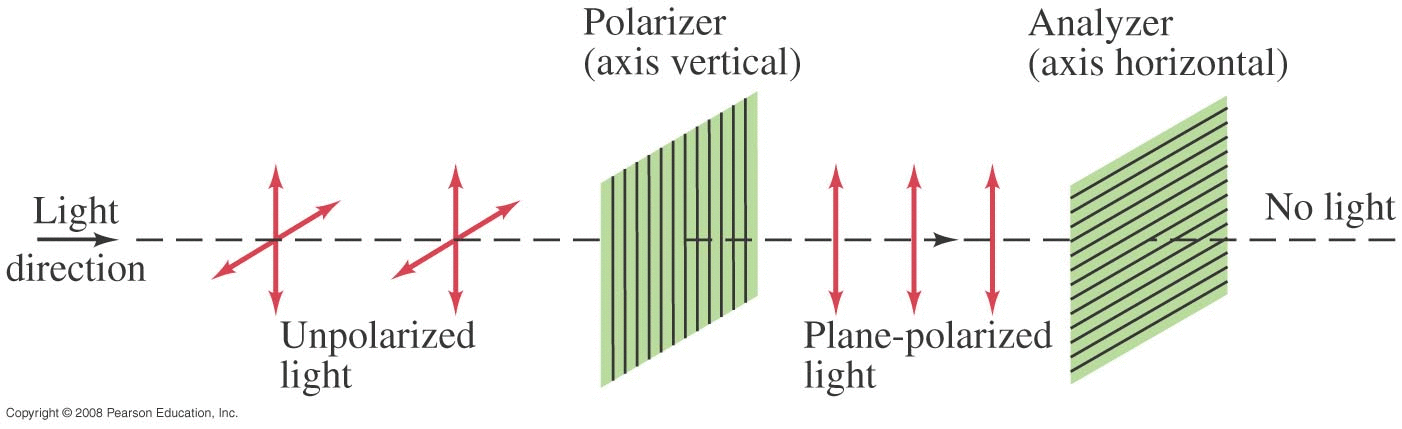
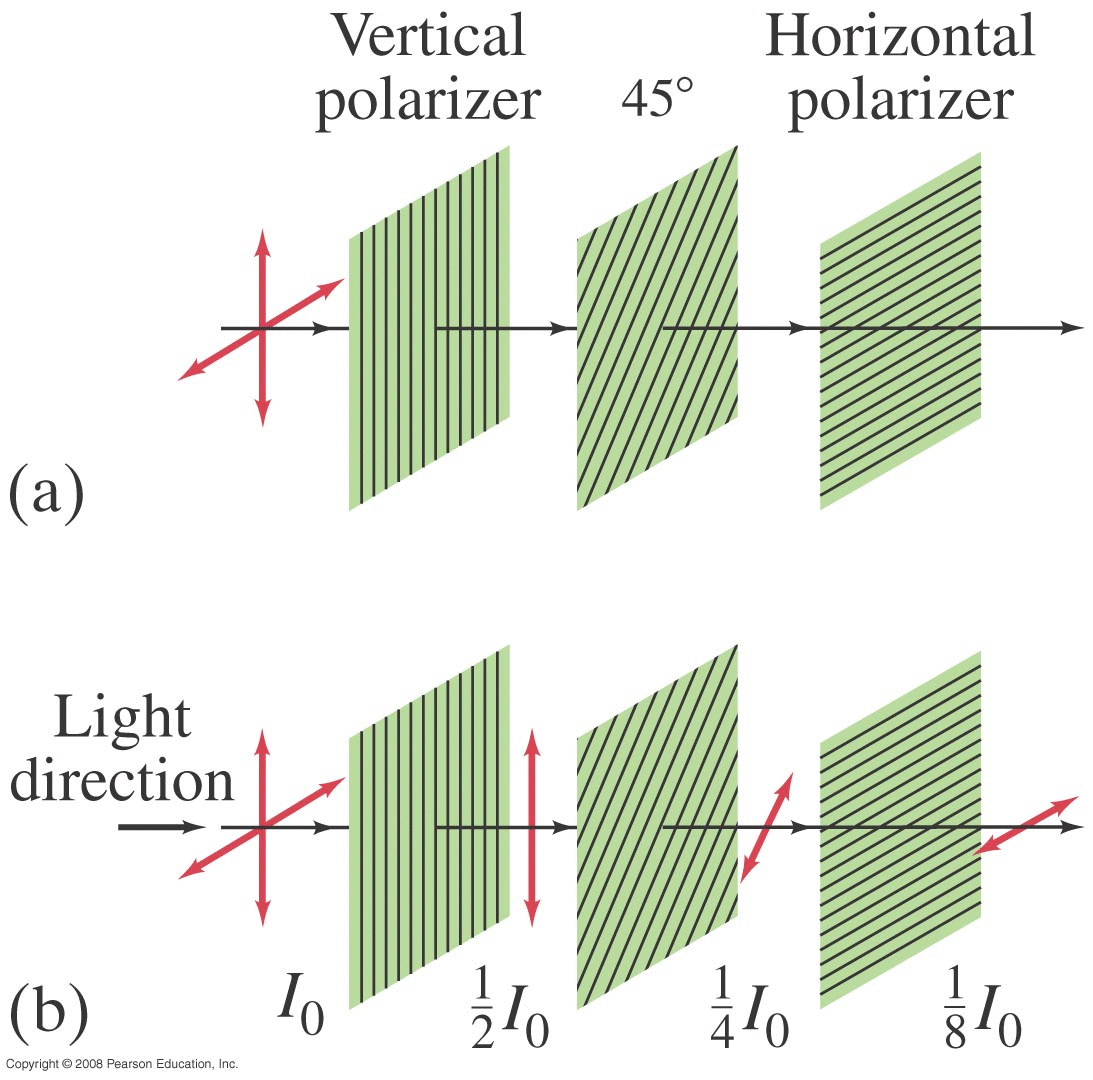
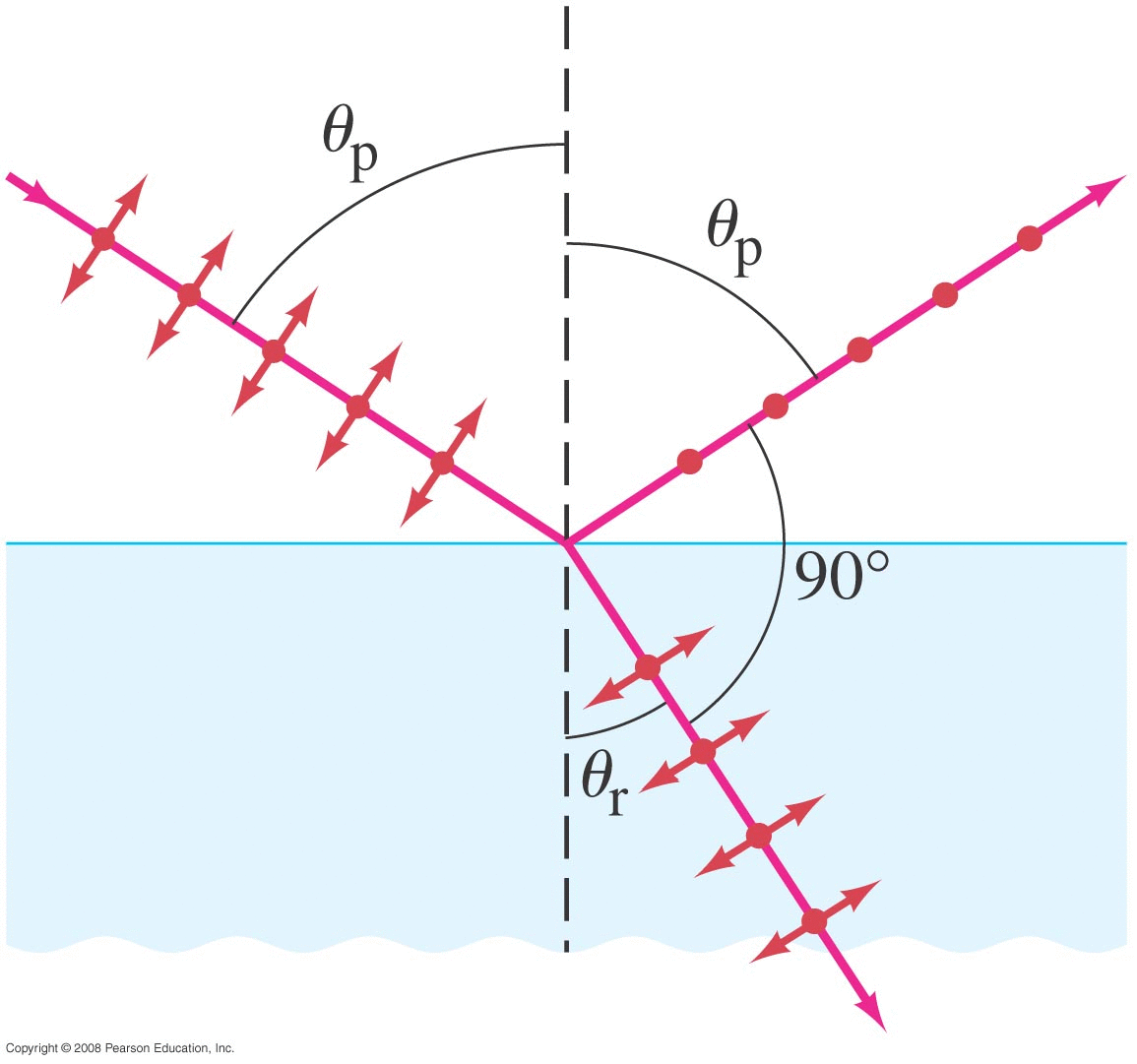
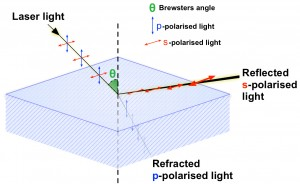
Thin Film (Summary)
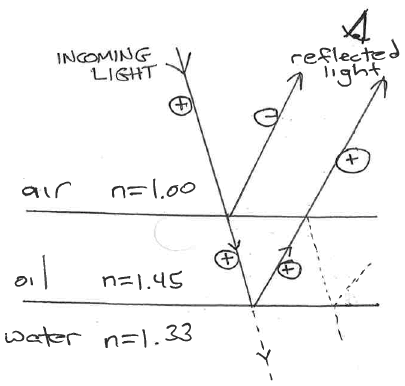
Reflected Ray : Ray reflecting off an interface:
• picks up a sign flip if reflecting off a higher 'n' material
• no sign change if reflecting off a lower 'n' material
Transmitted Ray : Ray passing through an interface:
• no sign change, no matter what the 'n' values are
Wavelength Changes while the photon is in the 'film'
• λfilm = λo/nfilm
IF THE REFLECTED RAYS HAVE THE SAME SIGN:
\[ 2t = (m)\lambda_{film} \hspace{3em} (constructive) \]
\[ 2t = (m+\frac{1}{2})\lambda_{film} \hspace{3em} (destructive) \]
IF THE REFLECTED RAYS HAVE OPPOSITE SIGNS:
\[ 2t = (m+\frac{1}{2})\lambda_{film} \hspace{3em} (constructive) \]
\[ 2t = (m)\lambda_{film} \hspace{3em} (destructive) \]
Which equation to use depends on BOTH:
• What is the film doing to the light?
• What do we want/need to happen to this light? (Equally important!)
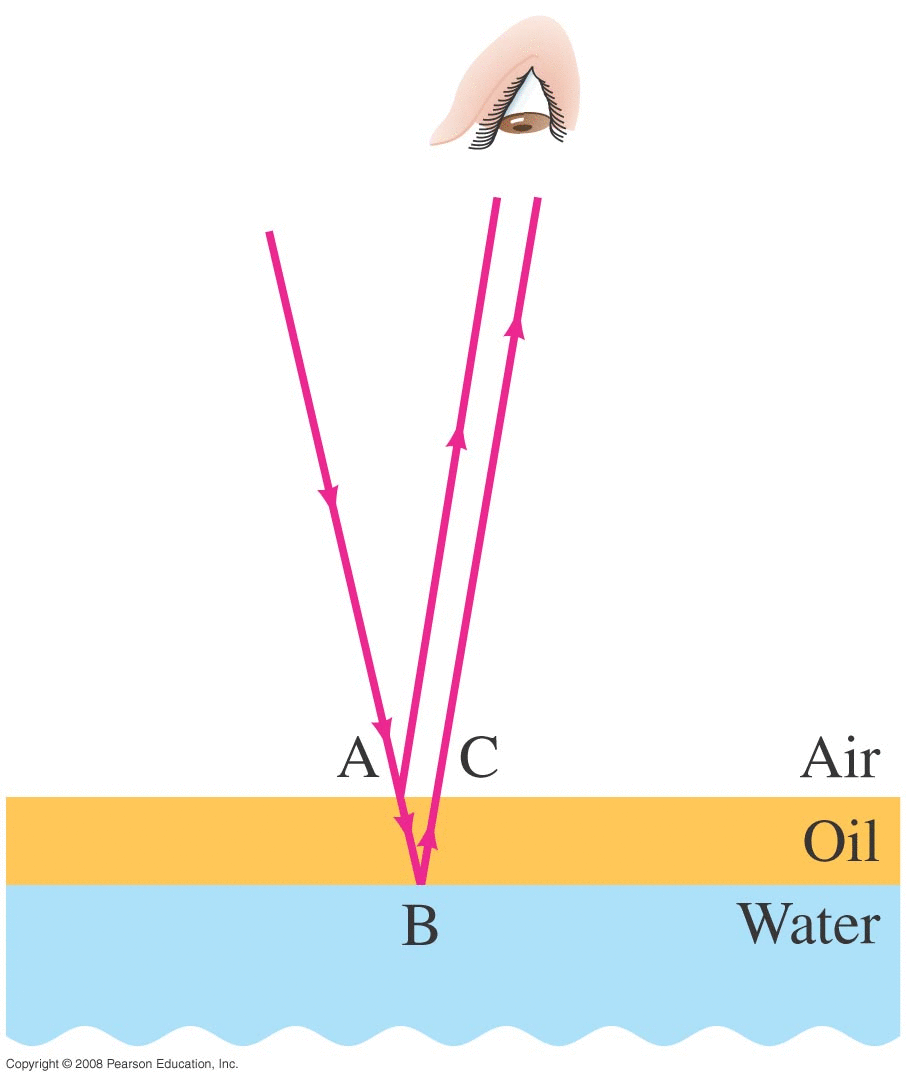
Lens Coating
Example (from Test 3 practice problems) :
A lens (made of glass with n=1.56) has a thin coating applied to it (the coating has an index of refraction of n=1.25).
When white light reflects off the lens it appears greenish-yellow (λ = 570 nm) in color.
How thick is the coating on the lens? (Give the thinnest two possible thicknesses it might be.) (Be sure to draw a diagram showing any sign-flip(s) involved here and be sure to explain how/why you decided to use the equation you chose to analyze this problem.)
Phone Screen Protector
Suppose we put this same film on our phone. What effect would it have? (The light source is coming from the phone screen itself now, passing through the glass, then hitting the film and then finally reaching our eyes.)
What colors (coming from the screen) would we see as extra bright or dim?
First Though : What equations would apply here? What equation would yield constructive interference for the light heading towards our eyes?
That seems like a pretty negative side effect of adding a screen protector to the phone. Why do we not see this effect?
Actual (plastic) screen protector thickness: 0.1 mm
Actual (glass) screen protector thickness: 0.3 mm to 0.5 mm
How many wavelengths does that represent?