Circular Aperture Diffraction
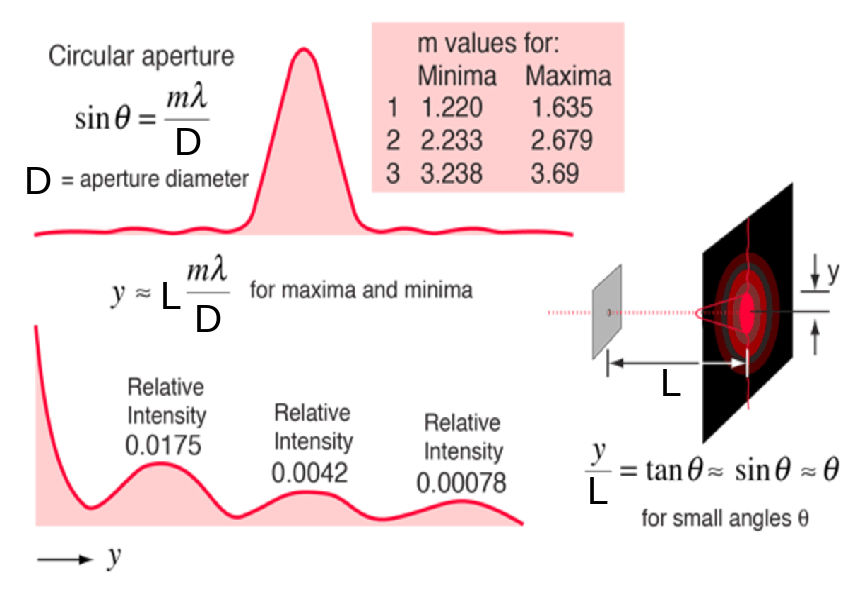
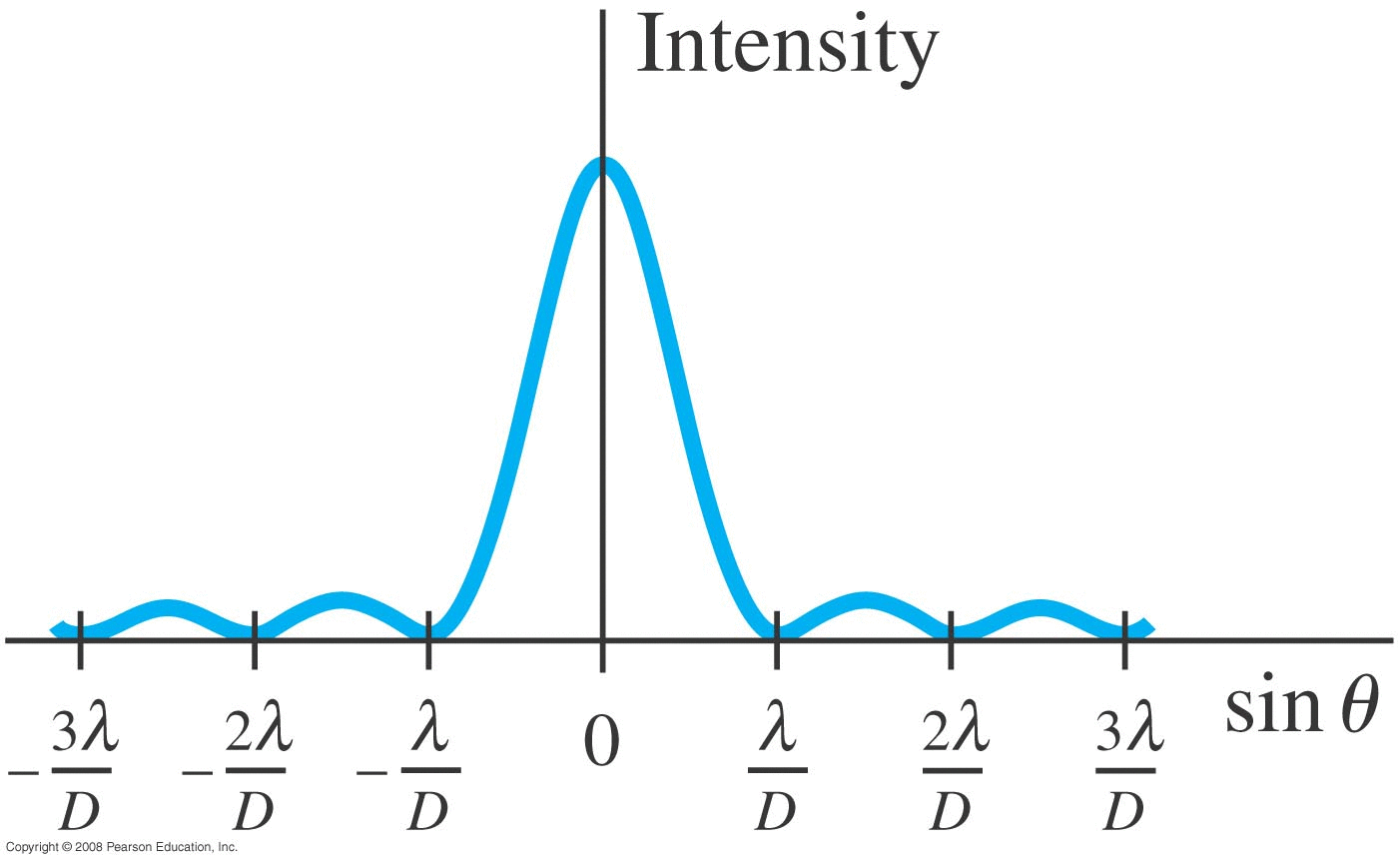
Sending a wave through a single slit-type aperture resulted in a simple intensity pattern involving the sinc function (squared), resulting in dark lines (no/low intensity, quiet sound, etc) where: sin(θ) = m ( λ/D ).
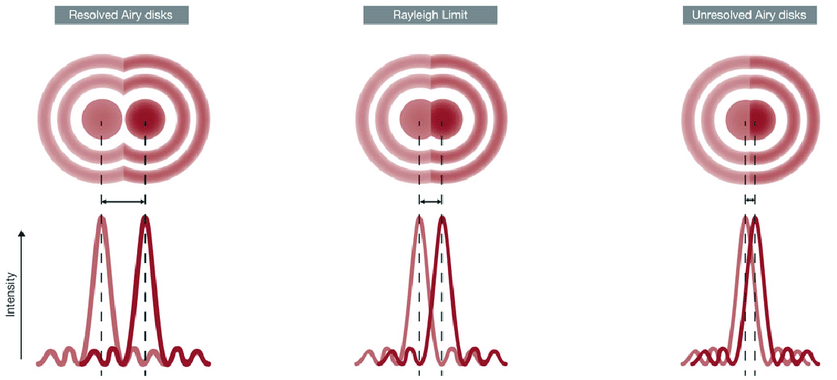
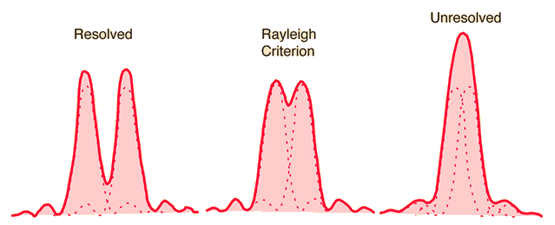
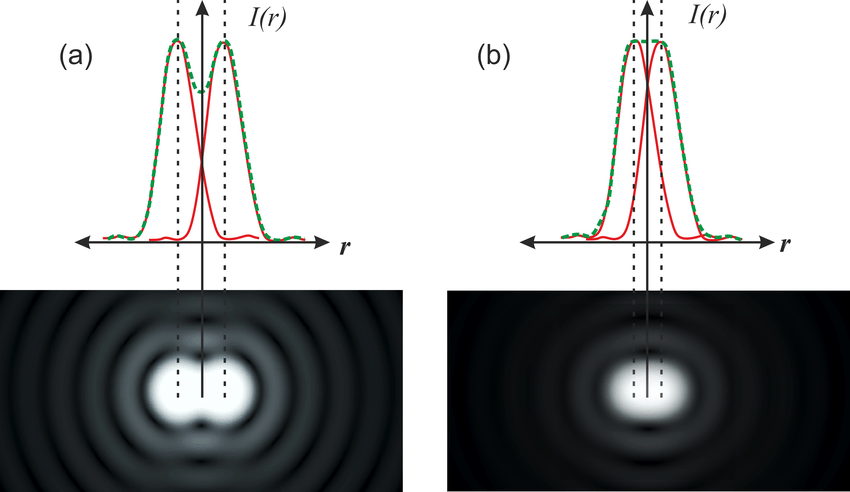
Suppose we send our waves through a circular aperture (hole). The integral is more difficult to do, but the result is similar except now we have radial symmetry resulting in an intensity pattern like shown on the right.     Mathematically the exact result involves a Bessel function which we won't do anything with directly.
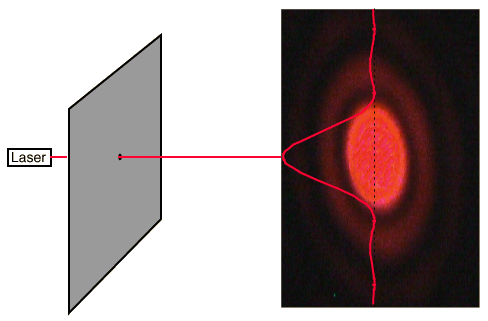
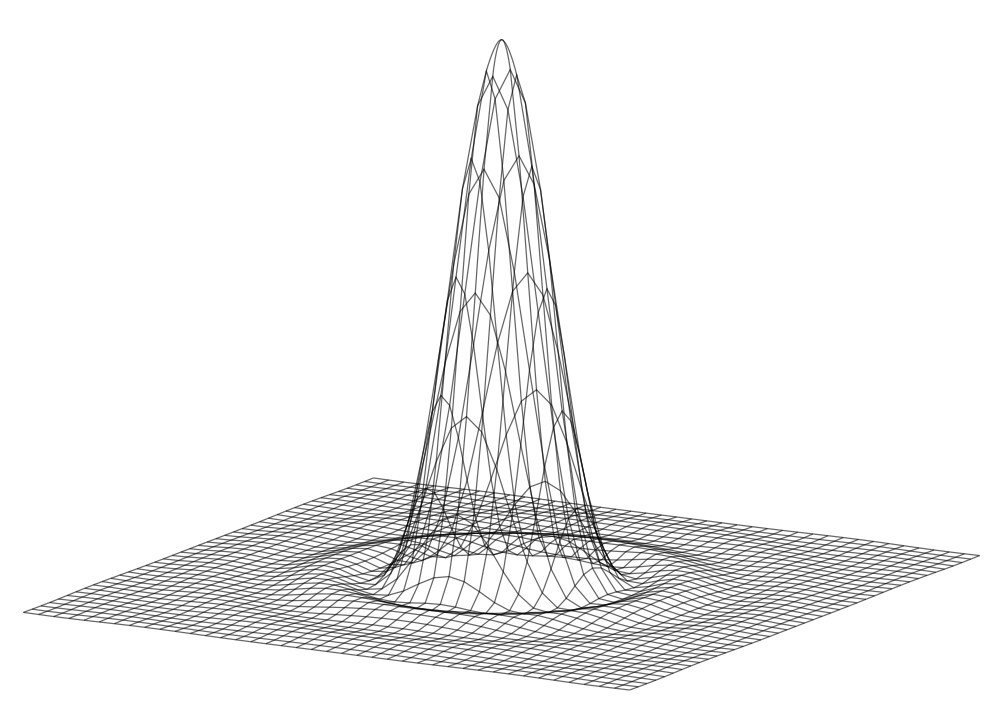
Theoretical and actual intensity with light passing through a tiny circular aperture.

 

Circular Aperture Intensity

The intensity still has a strong central part and rings of 'zero' intensity around it, and it's still common to write the angular 'location' of these dead spots (well rings now) in the form: sin(θ) = m ( λ/D )     BUT the m values aren't integers now:

 

 

Circular Aperture Effect on Lenses, Mirrors, etc
Recall the ray diagrams we drew to determine where an image would form for light passing through a lens. Unfortunately, each 'ray' is basically being spread out somewhat due to circular diffraction.
Here we follow two rays from a point on the object. Recall our magnification equation: \[ m = \frac{ h_i }{ h_o } = -\frac{ d_i }{d_o} \] which we can rewrite as: \[ |\frac{ h_i }{ d_i }| = |\frac{ h_o }{ d_o }| \]
If we follow the 'vertex rays' from two objects, we see that the angular size of the image is the same as the angular size of the object if we measure this angle relative to the LENS this time.
As the two objects get closer, their diffractions patterns start to overlap. If they are too close, the patterns overlap so much that we can no longer tell that there are two objects instead of just one.

 

Rayleigh Resolution Limit

We can still tell that two objects actually are two objects as long as their angular separation is such that the peak intensity of one is no closer than the first minimum in the intensity from the other object:   That is, their angular separation should be at least: sin(θmin) = 1.22λ/D   and since typically λ<<D : θmin = 1.22λ/D

 

Resolving Details in the Andromeda Galaxy
How close can two stars be in Andromeda and still be resolved as two separate entities? Use the Hubble telescope with D=2.40 m and assume a wavelength in the middle of the visible spectrum (λ=550 nm). Angular resolution of Hubble: \[ \theta_{min}=1.22\lambda/D = ?? \] Distance to Andromeda: 2.5 million light-years (LY)   Note : Average star-to-star distance around 5 LY in our area; roughly 0.013 LY near galactic center (which is about 200 times the distance from the Sun to Pluto). 1 LY = 5.88 X 1012 miles = 9.46 X 1015 m
Visible Light isn't the only way to observe objects.
This is picture of the Green Banks radio telescope that 'views' objects via their radio wave emissions. How far apart must objects be to be resolved when: D=110 m, and we are 'observing' at λ=21 cm?
Let's turn these two telescopes on Jupiter
What would Jupiter look like from Hubble in visible light? (I.e. what's the smallest detail we can 'see'?) What if we look at Jupiter with the radio telescope above? The radio picture of Jupiter (top picture below) was taken using an array of radio telescopes, effectively creating a single (radio) telescope with a much larger aperture (and therefore much smaller angular resolution).  •  diameter of Jupiter : 86400 miles  •  distance (closest approach) : 390 million miles

 

Hubble Resolution for various target objects
Let's point the Hubble telescope at various objects using the angular resolution we found above. How close can two things be at that distance and still be resolved as separate objects? Compare that to the (physical) diameter of the target: how many unique pixels of information do we actually have?
Earth's Moon : distance : 238850 miles smallest feature about 350 feet diameter of Moon : 2160 miles Best diffraction limited resolution 32300 X 32300 pixels       32000 pixels from edge to edge	Zooming in on some the crater features.
Mars : distance (closest approach) : 49 million miles smallest feature about 14 miles diameter of Mars : 4200 miles Best diffraction limited resolution 306 X 306 pixels
Jupiter : distance (closest approach) : 390 million miles smallest feature about 109 miles diameter of Jupiter : 86400 miles Best diffraction limited resolution 800 X 800 pixels
Saturn : distance (closest approach) : 800 million miles smallest feature about 224 miles diameter of Saturn : 72400 miles (just the planet) Best diffraction limited resolution 320 X 320 pixels
Pluto : distance (closest approach) : 3.3 billion miles smallest feature about 800 miles diameter of Pluto : 1480 miles Best diffraction limited resolution 2 X 2 pixels (!) The Hubble picture (rightmost) is a composite, averaging multiple images.

 

Hubble as a Spy Satellite
Suppose we turn Hubble towards Earth. How good would the picture be? Can we see faces? Read license plates? Orbit height: about 560 km.
Vehicle	Observed by Hubble

 

TV Screen Pixel Resolution
Suppose we have a large-ish TV with 1920 X 1080 pixels (called Full HD or 1080p) that is 1.2 m wide. (Note: That's the horizontal width; the diagonal here would be about 54 inches. These days, screens of this size would probably be 3840X2160 pixels, called 4K UHD or 2160p.)   How close is each pixel to the next? (called the 'pixel pitch') How far away do you need to sit to not be able to see individual pixels?
Staring at a bright screen, the diameter of the 'aperture' in the eye (the pupil) is about D=3 mm, so what is the angular resolution limit for the eye? \[ \theta_{min} = 1.22 \lambda / D \] (assume λ=550 nm, about the middle of the visible range)	The pixels in a TV (phone, tablet..) screen aren't single points of light but are made of multiple LED's.

 

Phone Resolution
Assuming you're holding a phone 25 cm from your eyes, how many pixels on a phone are 'enough' that we can't see the individual pixels (meaning the screen looks like a photograph)? What PPI (pixels per inch) would this be? How does this compare with the actual number of pixels on a phone?
According to wikipedia, my Pixel 6a has these parameters: Resolution: 2400 X 1080 Screen dimensions: 14.31 cm by 6.44 cm ~429 PPI (pixels per inch)
Various phones: Apple iPhone (11,12,...,16) : 458 to 460 PPI Google Pixel 8 Pro : 489 PPI Samsung Galaxy S7 : 577 PPI Sony Xperia 1 IV : 537 PPI Sony Xperia XZ Premium : 807 PPI (!)	Tablets are usually held farther away. Typical pixel densities for tablets range from 170 PPI to 350 PPI: iPad Air (2024) : 264 PPI iPad Mini (2024) : 326 PPI Samsung Galaxy Tab S9 Ultra : 266 PPI Microsoft Surface Pro 9 : 267 PPI
PPI calculator: https://rows.com/calculators/pixels-per-inch-calculator