Photon Momentum
Collision of (gamma ray) photons with electrons
Applying CoM and CoE requires photon to carry momentum, even though it has no mass. even though it has no mass
\[ p = \frac{E}{c} = \frac{hf}{c} = \frac{h}{\lambda} \]
\[ h = 6.62607015 \times 10^{-34}~J \cdot s \]
Example: Hydrogen
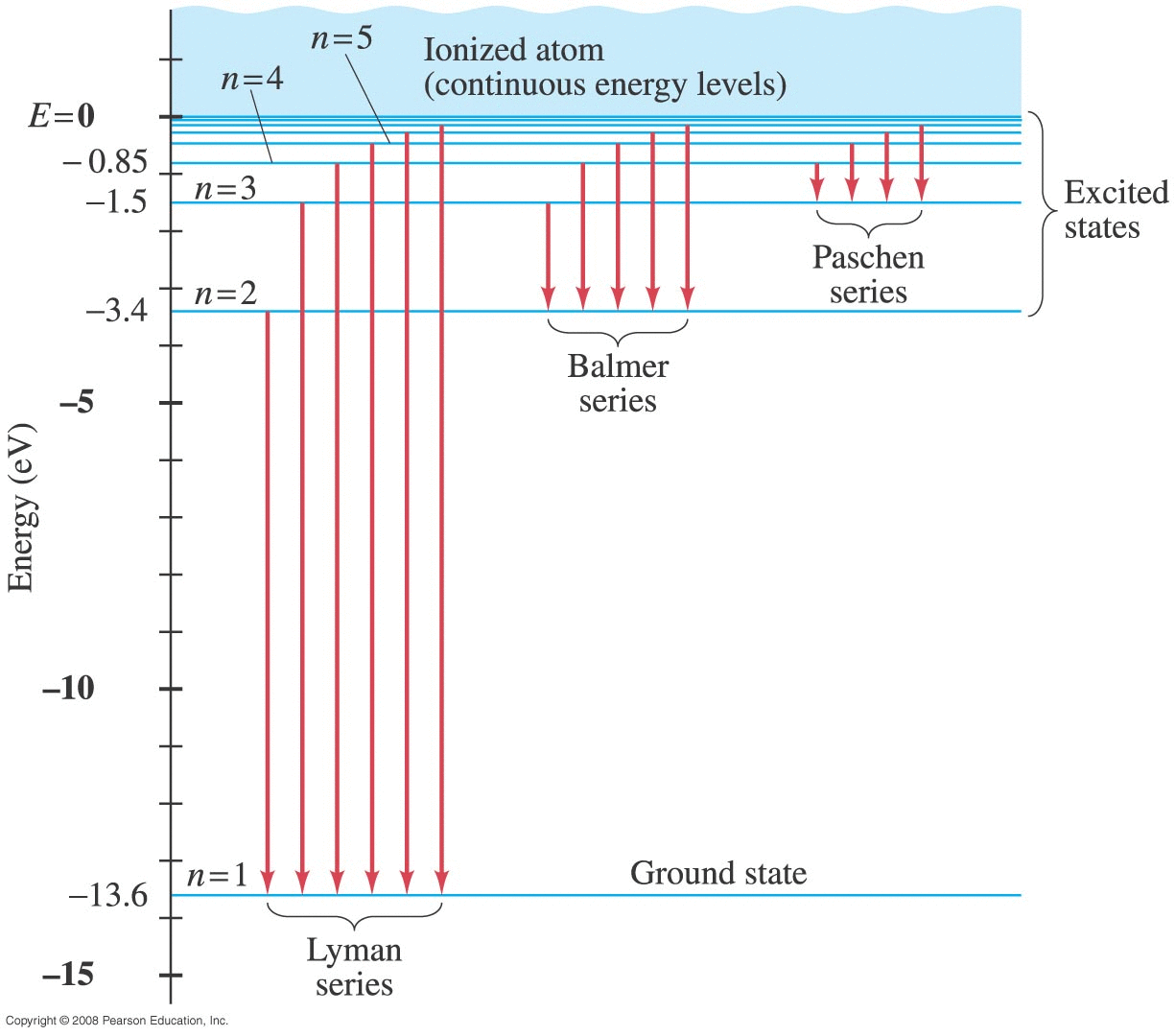
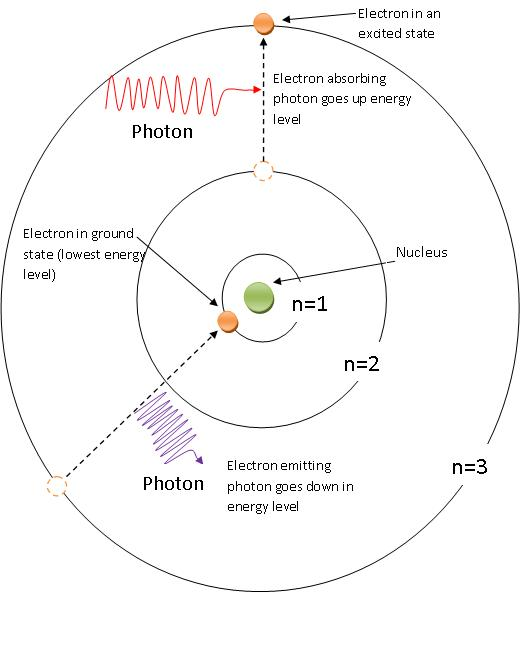
Recall Bohr model of the atom:
Previously found that if we have an atom with Z protons in the nucleus but just a single electron, the electron would have very specific energy levels:
\[ E_n = -( \frac{ Z^2 e^4 m }{ 8 \epsilon^2_o h^2 } ) \frac{1}{n^2} \]
Converting units:
\[ E_n = -(13.60569~eV) \frac{Z^2}{n^2} \]
Example : The lone electron in a hydrogen (Z=1) atom is presently in the n=3 orbit. It drops down to n=1, releasing a photon.
The photon will carry off energy and momentum.
The hydrogen atom will then recoil at what speed?
The moving hydrogen atom is also carrying off energy as a result.
How will this affect the wavelength of the emitted photon?
En = -(13.60569 eV) / n2
What energy photon will be released? (What wavelength? Visible?)
E = (1239.842 eV·nm)/λ (with wavelength in nm)What momentum would it have? p=E / c
Conservation of momentum : what speed must the H atom have?
mass of a single hydrogen atom:
1.007825 u where 1 u = 1.6605 × 10-27 kg
-
What kinetic energy does that represent?
-
Is that enough to affect the wavelength of the emitted photon?