Example 1

In this example, we have an object on a flat, frictionless surface. A rope is attached to it and an external force is applied to the rope to pull the block, and we want to calculate how fast it will accelerate.

(NOTE: the normal force is represented using the lowercase letter n here since that's what our previous textbook (and many other textbooks for that matter) used. Giancoli uses F_N.)

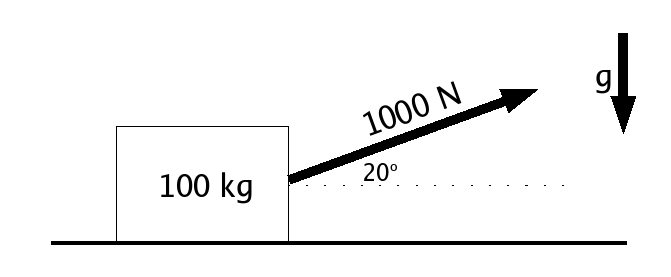
Step 1 : Account for all the forces acting on the object

Newton's Laws say that the vector sum of all the forces acting ON AN OBJECT is what produces the acceleration of THAT OBJECT. The first step of this process, then, is to determine all the forces that are acting on the object. Unless otherwise noted, we can infer that this object is on the Earth, so we know that gravity is acting downward resulting in a force of `mg' (in this case 980 N) `down'. The object is sitting on a surface that it can't pass through, so the surface (floor, ground, table-top, etc) is `pushing back' with a force called the normal force which acts perpendicular to the surface and directed away from it. Adding these two force vectors to the figure results in:

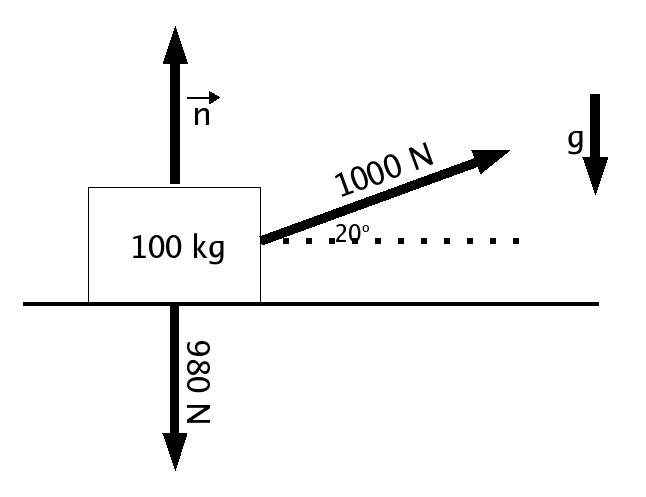
Step 2 : Define an appropriate coordinate system

Looking at the problem, we can see that the object will end up sliding along the floor and moving off to the right, so we'll define our +X axis to be in that direction, and let +Y point vertically upward.

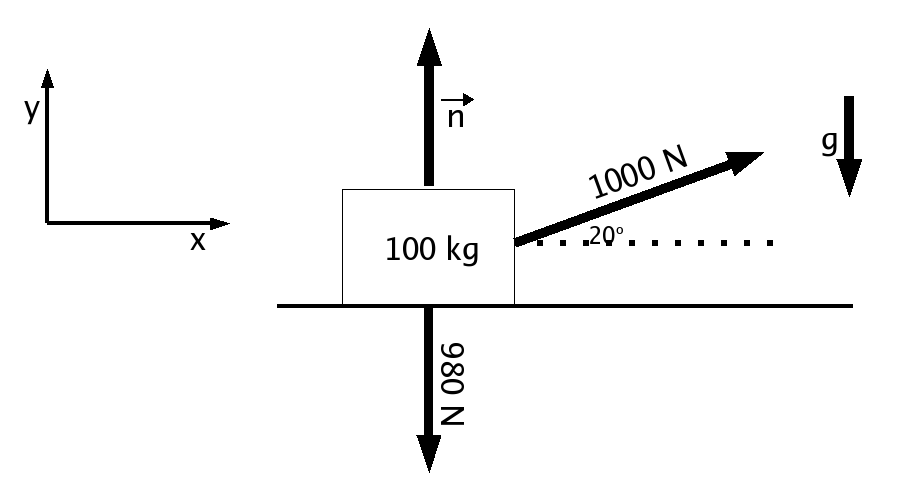
Step 3 : Convert all vectors into this new coordinate system

This is a critical step. We know that the sum of all the vector forces acting on the object is equal to the mass times the vector acceleration the object will undergo. This is a 2-D (or depending on the situation, 3-D) vector equation which might be fairly complicated to solve. But we know the block here is not going to be moving arbitrarily around in 3-D space: it is just going to be sliding along the floor in a line. That means it is really just 1-D motion, so we would like to come up with the F=ma equation in that direction alone. We also know that we can replace a vector by any two other vectors that add up to equal it, so this step involves replacing every force vector acting on the object with equivalent vectors that are aligned along the coordinate axes we chose. 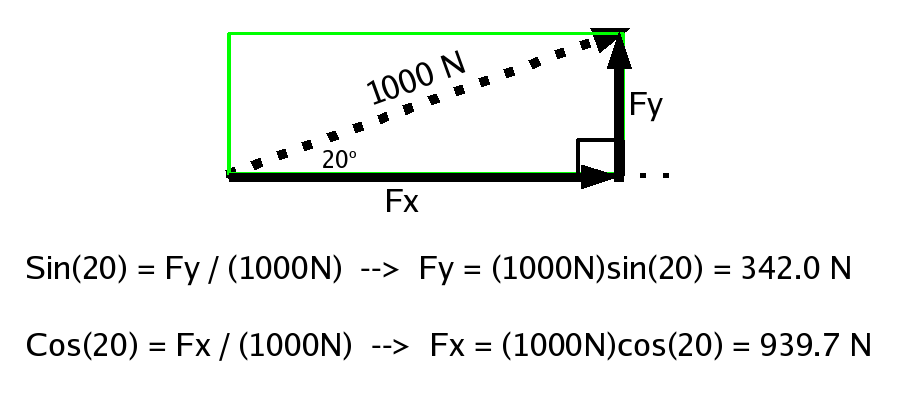In this example, the downward-acting weight of the object, and the normal force are already aligned along the Y axis, so we don't need to do anything to them. The 1000 N force is not lined up with either of the coordinate axes, though, so we need to convert this vector into two parts: one in the X direction and one in the Y direction. The first step here is to draw a little rectangle whose sides are parallel to the coordinate axes we defined, and which just surrounds the vector we are converting. The box should be placed so that the vector starts in one corner and ends in the opposite corner. One side of the rectangle that is aligned with the X axis gives us the component of the force in the X direction, and one side aligned with the Y axis gives us the component of the force in the Y direction. Now we can remove the original force (shown below as a dotted line) and replace it with these two vectors. The arrow heads should be placed so that these two vectors add up to the original one. We have now replaced the original force with two forces (one in each axis direction). The physics is completely unchanged by doing this: whether the object is being acted on by the single original force or these two new forces, it will behave in exactly the same way.

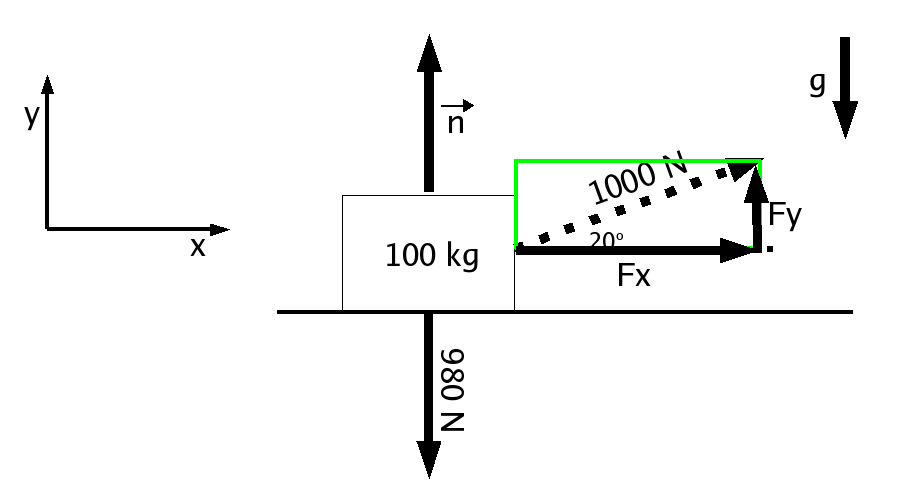
Step 4 : Solve for the magnitudes of the components

We need to solve for the magnitudes of these forces now. There is no general rule about whether sine or cosine or tangent or whatever might be used here. You'll need to look at the rectangle you drew and what angles you know or can infer and decide which trigonometric function you can use. In this case, we ended up with a right triangle whose hypoteneuse was 1000 N, and we knew the angle shown below, so here we can use the sine of that angle to determine the Y component and the cosine to find the X component.

Step 5 : Replace the original force with the components we just found

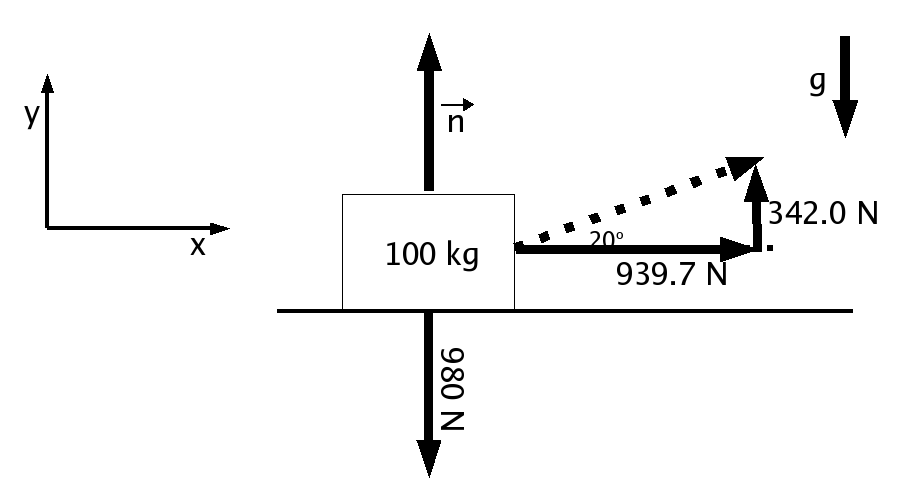
Now we can go back to our original figure and replace the 1000 N force at 20 degrees, by the two forces we just computed:

Step 6 : Repeat for all other forces acting on the object

In this particular example, the 1000 N force was the only one acting at an angle relative to the coordinate axes we chose, so we do not need to do anything else.

Step 7 : Solve F=ma in each direction

Now we can take the original F=ma vector equation and look at it separately in each direction.

Y direction : ΣF_y = ma_y

In this example, there is no friction, so we don't need to calculate the normal force, but if friction were present, we could find it now: in the Y direction, we have `n' pointing in the +Y direction, 342.0N also in the +Y direction (i.e. part of the 1000N external force we applied is acting in that direction) and 980 N in the -Y direction, and we know that the block cannot accelerate in that direction, so ΣF_y = ma_y becomes: +n+342-980=0 or n=980-342=638 N. (We would then use this value of the normal force to compute the kinetic or static friction, if present, but we don't have those in this example.)

X direction : ΣF_x = ma_x

In this example, the only force acting in the X direction is the 939.7 N, so F=ma in the X direction becomes: 939.7 N = (100 kg)(a) or a = 9.397 m/s^2.

Now that we know the acceleration of the block (and found that it is constant), we can use the equations of motion from earlier chapters to find how how fast it's moving after XX seconds, or after travelling XX meters to the right, and so on.